Reading plots of a complex function

This post is about understanding the following plot. If you’d like to read more along these lines, see [1].

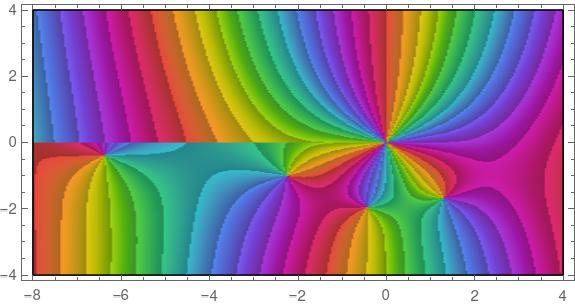
The plot was made with the following Mathematica command.

    ComplexPlot[HankelH1[3, z], {z, -8 - 4 I, 4 + 4 I}, 
        ColorFunction -> "CyclicArg", AspectRatio -> 1/2]

The plot uses color to represent the phase of the function values. If the output of the function is written in polar form as (r, θ), we’re seeing θ.

Here’s a plot of the identity function f(z) = z to show how the color rotation works.

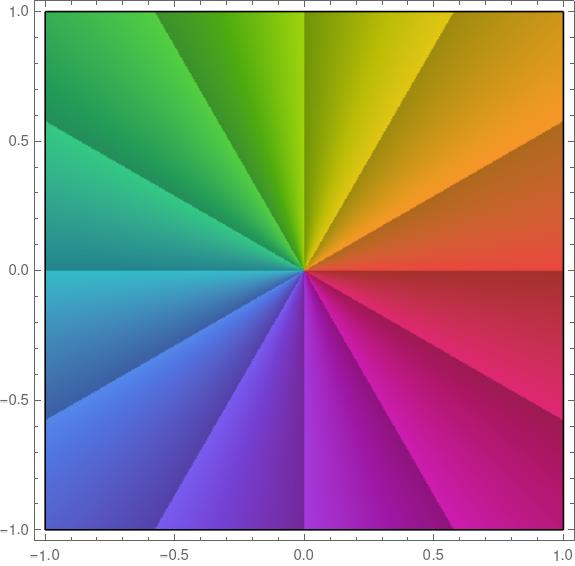
The color rotate from red to orange to green etc. (ROYGBIV) clockwise around a pole and counterclockwise around a zero.

You can see from the plot at the top that our function has a pole at 0. In fact, it’s a pole of order three because you go through the ROYGBIV cycle three times clockwise as you circle the origin.

You can also see four zeros, located near -6.4 – 0.4i, -2,2 – i, -0.4 -2i, and -1.3 – 1.7i. In each case we cycle through ROYGBIV one time counterclockwise, so these are simple zeros. If we had a double zero, we’d cycle through the colors twice. If we had a triple zero, we’d cycle through the colors three times, just as we did at the pole, except we’d go through the colors counterclockwise.

The colors in our plot vary continuously, except on the left side. There’s a discontinuity in our colors above and below the real axis. That’s because the function we’re plotting has a branch cut from -∞ to 0. The discontinuity isn’t noticeable near the origin, but it becomes more noticeable as you move away from the origin to the left.

Here’s a 3D plot to let us see the branch cut more clearly.

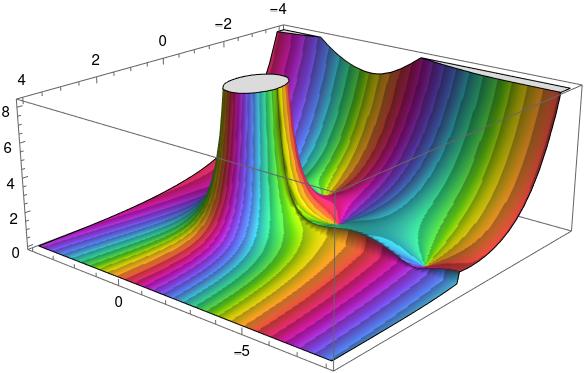
Here color represents phase as before, but now height represents absolute value, the r in our polar representation. The flat plateau on top is an artifact. The function becomes infinite at 0, so it had to be cut off.

You can see a seam in the graph. There’s a jump discontinuity along the negative real axis, with the function taking different values as you approach the real axis from the second quadrant or from the third quadrant.

This came up in a previous post, Architecture and math, but I didn’t say anything about it. Here’s a plot from that post.

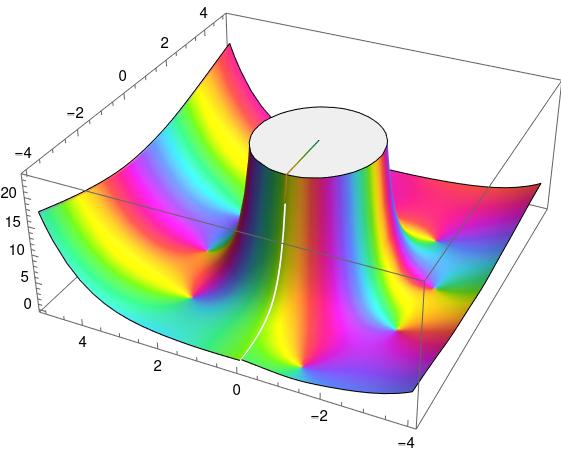
Why is there a little radial line on top where the graph was chopped off? And why is there a white streak below it? That’s evidence of a branch cut, though the discontinuity is small in this graph. You’ll notice color swirls around the base of the mesa. The colors swirl counterclockwise because they’re all at zeros. But you’ll notice the colors swirl clockwise as you go around the walls of the mesa. In fact they swirl around 5 times because there’s a pole of order 5 at the origin.

The book I mentioned in that post had something like this on the cover, plotting a generalization of the Hankel function. That’s why I chose the Hankel function as my example in this post.

Related posts

• Numbering the branches of the W function
• Marden’s amazing theorem
• Applied complex analysis

[1] Elias Wegert. Visual Complex Functions: An Introduction with Phase Portraits