Computing

Bessel, Everett, and Lagrange interpolation

Posted on by John

I never heard of Bessel or Everett interpolation until long after college. I saw Lagrange interpolation several times. Why Lagrange and not Bessel or Everett?

First of all, Bessel interpolation and Everett interpolation are not different kinds of interpolation; they are different algorithms for carrying out the same interpolation as Lagrange. There is a unique polynomial of degree n fitting a function at n + 1 points, and all three methods evaluate this same polynomial.

The advantages of Bessel’s approach or Everett’s approach to interpolation are practical, not theoretical. In particular, these algorithms are practical when interpolating functions from tables, by hand. This was a lost art by the time I went to college. Presumably some of the older faculty had spent hours computing with tables, but they never said anything about it.

Bessel interpolation and Everett interpolation are minor variations on the same theme. This post will describe both at such a high level that there’s no difference between them. This post is high-level because that’s exactly what seems to be missing in the literature. You can easily find older books that go into great detail, but I believe you’ll have a harder time finding a survey presentation like this.

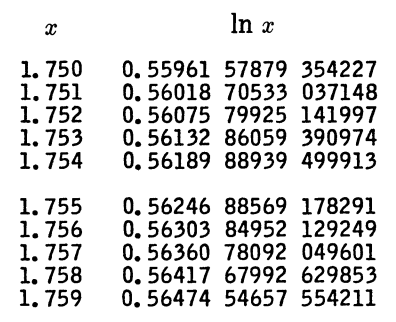
Suppose you have a function f(x) that you want to evaluate at some value p. Without loss of generality we can assume our function has been shifted and scaled so that we have tabulated f at integers our value p lies between 0 and 1.

Everett’s formula (and Bessel’s) cleanly separates the parts of the interpolation formula that depend on f and the parts that depend on p.

The values of the function f enter through the differences of the values of f at consecutive integers, and differences of these differences, etc. These differences are easy to calculate by hand, and sometimes were provided by the table publisher.

The functions of p are independent of the function being interpolated, so these functions, the coefficients in Bessel’s formula and Everett’s formula, could be tabulated as well.

If the function differences are tabulated, and the functions that depend on p are tabulated, you could apply polynomial interpolation without ever having to explicitly evaluate a polynomial. You’d just need to evaluate a sort of dot product, a sum of numbers that depend on f multiplied by numbers that depend on p.

Another advantage of Bessel’s and Everett’s interpolation formulas is that they can be seen as a sequence of refinements. First you obtain the linear interpolation result, then refine it to get the quadratic interpolation result, then add terms to get the cubic interpolation result, etc.

This has several advantages. First, you have the satisfaction of seeing progress along the way; Lagrange interpolation may give you nothing useful until you’re done. Related to this is a kind of error checking: you have a sense of where the calculations are going, and intermediate results that violate your expectations are likely to be errors. Finally, you can carry out the calculations for the smallest terms in with less precision. You can use fewer and fewer digits in your hand calculations as you compute successive refinements to your result.

Related posts

Compression and interpolation

Posted on by John

Data compression is everywhere. We’re unaware of it when it is done well. We only become aware of it when it is pushed too far, such as when a photo looks grainy or fuzzy because it was compressed too much.

The basic idea of data compression is to not transmit the raw data but to transmit some of the data along with instructions for how to approximately reconstruct the rest [1].

Fifty years ago scientists were concerned with a different application of compression: reducing the size of mathematical tables. Books of tabulated functions are obsolete now, but the principles used in producing these tables are still very much relevant. We use compression and interpolation far more often now, though it’s almost always invisibly executed by software.

Compressing tables

In this post I want to expand on comments by Forman Acton from his book Numerical Methods That Work on compression.

Many persons are unaware of the considerable compression in a table that even the use of quadratic interpolation permits. A table of sin x covering the first quadrant, for example, requires 541 pages if it is to be linearly interpolable to eight decimal places. If quadratic interpolation is used, the same table takes only one page having entries at one-degree intervals with functions of the first and second differences being recorded together with the sine itself.

Acton goes on to mention the advantage of condensing shelf space by a factor of 500. We no longer care about saving shelf space, but we may care very much about saving memory in an embedded device.

Quadratic interpolation does allow more compression than linear interpolation, but not by a factor of 500. I admire Acton’s numerical methods book, but I’m afraid he got this one wrong.

Interpolation error bound

In order to test Acton’s claim we will need the following theorem on interpolation error [2].

Let f be a function so that f(n+1) is continuous on [a, b] and satisfies |f(n+1) (x)| ≤ M. Let p be the polynomial of degree ≤ n that interpolates f at n + 1 equally spaced nodes in [a, b], including the end points. Then on [a, b],

|f(x) - p(x)| \leq \frac{1}{4(n+1)} M \left(\frac{b-a}{n}\right)^{n+1}

Quadratic interpolation error

Acton claims that quadratic interpolation at intervals of one degree is adequate to produce eight decimal places of accuracy. Quadratic interpolation means n = 2.

We have our function tabulated at evenly spaced points a distance h = π/180 radians apart. Quadratic interpolation requires function values at three points, so b − a = 2h = π/90. The third derivative of sine is negative cosine, so M = 1.

This gives an error bound of 4.43 × 10−7, so this would give slightly better than six decimal place accuracy, not eight.

Linear interpolation error

Suppose we wanted to create a table of sine values so that linear interpolation would give results accurate to eight decimal places.
In the interpolation error formula we have M = 1 as before, and now n = 1. We would need to tabulate sine at enough points that h = b − a is small enough that the error is less than 5 × 10−9. It follows that h = 0.0002 radians. Covering a range of π/2 radians in increments of 0.0002 radians would require 7854 function values. Acton implicitly assumes 90 values to a page, so this would take about 87 pages.

Abramowitz and Stegun devotes 32 pages to tabulating sine and cosine at increments of 0.001 radian. This does not always guarantee eight decimal place accuracy using linear interpolation, but it does guarantee at least seven places (more on that here), which is better than a table at one degree increments would deliver using quadratic interpolation. So it would have been more accurate for Acton to say quadratic interpolation reduces the number of pages by a factor of 30 rather than 500.

Cubic interpolation error

If we have a table of sine values at one degree increments, how much accuracy could we get using cubic interpolation? In that case we’d apply the interpolation error theorem with n = 3 and b − a = 3(π/180) = π/60. Then the error bound is 5.8 × 10−9. This would usually give you eight decimal place accuracy, so perhaps Acton carried out the calculation for cubic interpolation rather than quadratic interpolation.

Related posts

[1] This is what’s known as lossy compression; some information is lost in the compression process. Lossless compression also replaces the original data with a description that can be used to reproduce the data, but in this case the reconstruction process is perfect.

[2] Ward Cheney and David Kincaid. Numerical Methods and Computation. Third edition.

 

Math’s base 32 versus Linux’s base 32

Posted on by John

The convention in math for writing numbers in bases larger than 10 is to insert capital letters after 9, starting with A. So, for example, the digits in base 12 are 0, 1, 2, …, 9, A, and B.

So if you’re familiar with math but not Linux, and you run across the base32 utility, you might naturally assume that the command converts numbers to base 32 using the symbols 0, 1, 2, &hellip, 9, A, B, C, …, V. That’s a reasonable guess, but it actually uses the symbols A, B, C, …, Z, 2, 3, 4, 5, 6, and 7. It’s all described in RFC 3548.

What’s going on? The purpose of base 32 encoding is to render binary data in a way that is human readable and capable of being processed by software that was originally written with human readable input in mind. The purpose is not to carry out mathematical operations.

Note that the digit 0 is not used, because it’s visually similar to the letter O. The digit 1 is also not used, perhaps because it looks like a lowercase l in some fonts.

Related posts

Editing a file without an editor

Posted on by John

I don’t use sed very often, but it’s very handy when I do use it, particularly when needing to make a small change to a large file.

Fixing a JSON file

Lately I’ve been trying to fix a 30 MB JSON file that has been corrupted somehow. The file is one very long line.

Emacs was unable to open the file. (It might have eventually opened the file, but I killed the process when it took longer than I was willing to wait.)

Emacs can open large files, but it has trouble with long lines. Somewhere its data structures assume lines are not typically millions of characters long.

I used sed to add line breaks after closing brackets

    sed -i 's/]/]\n/g' myfile.json

and then I was able to open the file in Emacs.

If the problem with my JSON file were simply a missing closing brace—it’s not—then I could add a closing brace with

    sed -i 's/$/}/' myfile.json

Using sed to find a job

I had a friend in college who got a job because of a sed script he wrote as an intern.

A finite element program would crash when it attempted to take too large a time step, but the program would not finish by the time the results were needed if it always took tiny time steps. So they’d let the program crash occasionally, then edit the configuration file with a smaller time step and restart the program.

They were asking engineers to work around the clock so someone could edit the configuration file and restart the finite element program if it crashed in the middle of the night. My friend wrote a shell script to automate this process, using sed to do the file editing. He eliminated the need for a night shift and got a job offer.

Related posts

National Provider Identifier (NPI) and its checksum

Posted on by John

Healthcare providers in the United States are required to have an ID number known as the NPI (National Provider Identifier). This is a 10-digit unique identifier which serves as the primary key in a publicly available database. You can use the NPI number to look up a provider’s name, credentials, their practice location, etc. The use of NPI numbers was required by HIPAA.

The specification for the NPI number format says that the first digit must be either 1 or 2. Currently every NPI in the database starts with 1. There are about 8.4 million NPIs currently, so it’ll be a while before they’ll need to roll the first digit over to 2.

The last digit of the NPI is a check sum. The check sum uses the Luhn algorithm, the same check sum used for credit cards and other kinds of identifiers. The Luhn algorithm was developed in 1954 and was designed to be easy to implement by hand. It’s kind of a quirky algorithm, but it will catch all single-digit errors and nearly all transposition errors.

The Luhn algorithm is not applied to the NPI itself but by first prepending 80840 to the (first nine digits of) the NPI.

For example, let’s look at 1993999998. This is not (currently) anyone’s NPI, but it has a valid NPI format because the Luhn checksum of 80840199399999 is 8. We will verify this with the code below.

Python code for Luhn checksum

The following code computes the Luhn checksum.

    def checksum(payload):
        digits = [int(c) for c in reversed(str(payload))]
        s = 0
        for i, d in enumerate(digits):
            if i % 2 == 0:
                t = 2*d
                if t > 9:
                    t -= 9
                s += t
            else:
                s += d
        return (s*9) % 10

And the following checks whether the last digit of a number is the checksum of the previous digits.

    def verify(fullnumber):
        payload = fullnumber // 10
        return checksum(payload) == fullnumber % 10

And finally, the following validates an NPI number.

    def verify_npi(npi):
        return verify(int("80840" + str(npi)))

Here we apply the code above to the hypothetical NPI number mentioned above.

    assert(checksum(80840199399999) == 8)
    assert(verify(808401993999998))
    assert(verify_npi(1993999998))

Related posts

Getting some (algorithmic) SAT-isfaction

Posted on by Wayne Joubert

How can you possibly solve a mission-critical problem with millions of variables—when the worst-case computational complexity of every known algorithm for that problem is exponential in the number of variables?

SAT (Satisfiability) solvers have seen dramatic orders-of-magnitude performance gains for many problems through algorithmic improvements over the last couple of decades or so. The SAT problem—finding an assignment of Boolean variables that makes a given Boolean expression true—represents the archetypal NP-complete problem and in the general case is intractable.

However, for many practical problems, solutions can be found very efficiently by use of modern methods. This “killer app” of computer science, as described by Donald Knuth, has applications to many areas, including software verification, electronic design automation, artificial intelligence, bioinformatics, and planning and scheduling.

Its uses are surprising and diverse, from running billion dollar auctions to solving graph coloring problems to computing solutions to Sudoku puzzles. As an example, I’ve included a toy code below that uses SMT, a relative of SAT, to find the English language suffix rule for regular past tense verbs (“-ed”) from data.

When used as a machine learning method, SAT solvers are quite different from other methods such as neural networks. SAT solvers can for some problems have long or unpredictable runtimes (though MAXSAT can sometimes relax this restriction), whereas neural networks have essentially fixed inference cost (though looping agent-based models do not).

On the other hand, answers from SAT solvers are always guaranteed correct, and the process is interpretable; this is currently not so for neural network-based large language models.

To understand better how to think about this difference in method capabilities, we can take a lesson from the computational science community. There, it is common to have a well-stocked computational toolbox of both slow, accurate methods and fast, approximate methods.

In computational chemistry, ab initio methods can give highly accurate results by solving Schrödinger’s equation directly, but only scale to limited numbers of atoms. Molecular dynamics (MD), however, relies more on approximations, but scales efficiently to many more atoms. Both are useful in different contexts. In fact, the two methodologies can cross-pollenate, for example when ab initio calculations are used to devise force fields for MD simulations.

A lesson to take from this is, it is paramount to find the best tool for the given problem, using any and all means at one’s disposal.

The following are some of my favorite general references on SAT solvers:

It would seem that unless P = NP, commonly suspected to be false, the solution of these kinds of problems for any possible input is hopelessly beyond reach of even the world’s fastest computers. Thankfully, many of the problems we care about have an internal structure that makes them much more solvable (and likewise for neural networks). Continued improvement of SAT/SMT methods, in theory and implementation, will greatly benefit the effective solution of these problems.

A toy example: find the English past tense suffix rule using Z3

import csv
import z3

def char2int(c): return ord(c) - ord('a')

def int2char(i): return chr(i + ord('a'))

# Access the language data from the file.
with open('eng_cols.txt', newline='') as csvfile:
    reader = csv.reader(csvfile, delimiter='\t')
    table = [row for row in reader]

nrow, ncol = len(table), len(table[0])

# Identify which columns of input table have stem and targeted word form.
stem_col, form_col = 0, 1

# Calculate word lengths.
nstem = [len(table[i][stem_col]) for i in range(nrow)]
nform = [len(table[i][form_col]) for i in range(nrow)]

# Length of suffix being sought.
ns = 2

# Initialize optimizer.
solver = z3.Optimize()

# Define variables to identify the characters of suffix; add constraints.
var_suf = [z3.Int(f'var_suf_{i}') for i in range(ns)]

for i in range(ns):
    solver.add(z3.And(var_suf[i] >= 0, var_suf[i] < 26))

# Define variables to indicate whether the given word matches the rule.
var_m = [z3.Bool(f'var_m_{i}') for i in range(nrow)]

# Loop over words.
for i in range(nrow):

    # Constraint on number of characters.
    constraints = [nform[i] == nstem[i] + ns]

    # Constraint that the form contains the stem.
    for j in range(nstem[i]):
        constraints.append(
            table[i][stem_col][j] == table[i][form_col][j]
                if j < nform[i] else False)

    # Constraint that the end of the word form matches the suffix. 
    for j in range(ns):
        constraints.append(
            char2int(table[i][form_col][nform[i]-1-j]) == var_suf[j]
                if j < nform[i] else False)

    # var_m[i] is the "and" of all these constraints.
    solver.add(var_m[i] == z3.And(constraints))

# Seek suffix that maximizes number of matches.
count = z3.Sum([z3.If(var_m[i], 1, 0) for i in range(nrow)])
solver.maximize(count)

# Run solver, output results.
if solver.check() == z3.sat:
    model = solver.model()
    suf = [model[var_suf[i]] for i in range(ns)]
    print('Suffix identified: ' +
          ''.join(list([int2char(suf[i].as_long())
                        for i in range(ns)]))[::-1])
    print('Number of matches: ' + str(model.evaluate(count)) +
          ' out of ' + str(nrow) + '.')

    var_m_values = [model[var_m[i]] for i in range(nrow)]

    print('Matches:')
    for i in range(nrow):
        if var_m_values[i]:
            print(table[i][stem_col], table[i][form_col])

Calculating trig functions from tables

Posted on by John

It takes some skill to use tables of mathematical functions; it’s not quite as simple as it may seem. Although it’s no longer necessary to use tables, it’s interesting to look into the details of how it is done.

For example, the Handbook of Mathematical Functions edited by Abramowitz and Stegun tabulates sines and cosines in increments of one tenth of a degree, from 0 degrees to 45 degrees. What if your angle was outside the range 0° to 45° or if you needed to specify your angle more precisely than 1/10 of a degree? What if you wanted, for example, to calculate cos 203.147°?

The high-level answer is that you would use range reduction and interpolation. You’d first use range reduction to reduce the problem of working with any angle to the problem of working with an angle between 0° and 45°, then you’d use interpolation to get the necessary accuracy for a value within this range.

OK, but how exactly do you do the range reduction and how exactly do you to the interpolation? This isn’t deep, but it’s not trivial either.

Range reduction

Since sine and cosine have a period of 360°, you can add or subtract some multiple of 360° to obtain an angle between −180° and 180°.

Next, you can use parity to reduce the range further. That is, since sin(−x) = −sin(x) and cos(−x) = cos(x) you can reduce the problem to computing the sine or cosine of an angle between 0 and 180°.

The identities sin(180° − x) = sin(x) and cos(180° −x) = −cos(x) let you reduce the range further to between 0 and 90°.

Finally, the identities cos(x) = sin(90° − x) and sin(x) = cos(90° − x) can reduce the range to 0° to 45°.

Interpolation

You can fill in between the tabulated angles using interpolation, but how accurate will your result be? How many interpolation points will you need to use in order to get single precision, e.g. an error on the order of 10−7?

The tables tell you. As explained in this post on using a table of logarithms, the tables have a notation at the bottom of the table that tells you how many Lagrange interpolation points to use and what kind of accuracy you’ll get. Five interpolation points will give you roughly single precision accuracy, and the notation gives you a little more accurate error bound. The post on using log tables also explains how Lagrange interpolation works.

Beyond trig functions

I intend to write more posts on using tables. The general pattern is always range reduction and interpolation, but it takes more advanced math to reduce the range of more advanced functions.

Update: The next post shows how to use tables to compute the gamma function for complex arguments.

Using a table of logarithms

Posted on by John

My favorite quote from Richard Feynman is his remark that “nearly everything is really interesting if you go into it deeply enough.” This post will look at something that seems utterly trivial—looking up numbers in a table—and show that there’s much more to it when you dig a little deeper.

More than just looking up numbers

Before calculators were common, function values would be looked up in a table. For example, here is a piece of a table of logarithms from Abramowitz and Stegun, affectionately known as A&S.

But you wouldn’t just “look up” logarithm values. If you needed to know the value of a logarithm at a point where it is explicitly tabulated, then yes, you’d simply look it up. If you wanted to know the log of 1.754, then there it is in the table. But what if, for example, you wanted to know the log of 1.7543?

Notice that function values are given to 15 significant figures but input values are only given to four significant figures. If you wanted 15 sig figs in your output, presumably you’d want to specify your input to 15 sig figs as well. Or maybe you only needed 10 figures of precision, in which case you could ignore the rightmost column of decimal places in the table, but you still can’t directly specify input values to 10 figures.

Lagrange interpolation

If you go to the bottom of the column of A&S in the image above, you see this:

What’s the meaning of the mysterious square bracket expression? It’s telling you that for the input values in the range of this column, i.e. between 1.750 and 1.800, the error using linear interpolation will be less than 4 × 10−8, and that if you want full precision, i.e. 15 sig figs, then you’ll need to use Lagrange interpolation with 5 points.

So going back to the example of wanting to know the value of log(1,7543), we could calculate it using

0.7 × log(1.754) + 0.3 × log(1.755)

and expect the error to be less than 4 × 10−8.

We can confirm this with a little Python code.

>>> from math import log
>>> exact = log(1.7543)
>>> approx = 0.7*log(1.754) + 0.3*log(1.755)
>>> exact - approx
3.411265947494968e-08

Python uses double precision arithmetic, which is accurate to between 15 and 16 figures—more on that here—and so the function calls above are essentially the same as the tabulated values.

Now suppose we want the value of x = 1.75430123456789. The hint in square brackets says we should use Lagrange interpolation at five points, centered at the nearest tabulated value to x. That is, we’ll use the values of log at 1.752, 1.753, 1.754, 1.755, and 1.756 to compute the value of log(x).

Here’s the Lagrange interpolation formula, given in A&S as equation 25.2.15.

We illustrate this with the following Python code.

def interpolate(fs, p, h):
    s = (p**2 - 1)*p*(p-2)*fs[0]/24
    s -= (p - 1)*p*(p**2 - 4)*fs[1]/6
    s += (p**2 - 1)*(p**2 - 4)*fs[2]/4
    s -= (p + 1)*p*(p**2 - 4)*fs[3]/6
    s += (p**2 - 1)*p*(p + 2)*fs[4]/24
    return s

xs = np.linspace(1.752, 1.756, 5)
fs = np.log(xs)
h = 0.001
x = 1.75430123456789
p = (x - 1.754)/h

print(interpolate(fs, p, h))
print(np.log(x))

This prints

0.5620706206909348
0.5620706206909349

confirming that the interpolated value is indeed accurate to 15 figures.

Lagrange interpolation takes a lot of work to carry out by hand, and so sometimes you might use other techniques, such as transforming your calculation into one for which a Taylor series approximation converges quickly. In any case, sophisticated use of numerical tables was not simply a matter of looking things up.

Contemporary applications

A book of numerical tables enables you to do calculations without a computer. More than that, understanding how to do calculations without a computer helps you program calculations with a computer. Computers have to evaluate functions somehow, and one way is interpolating tabulated values.

For example, you could think of a digital image as a numerical table, the values of some ideal analog image sampled at discrete points. The screenshots above are interpolated: the HTML specifies the width to be less than that of the original screenshots,. You’re not seeing the original image; you’re seeing a new image that your computer has created for you using interpolation.

Interpolation is a kind of compression. A&S would be 100 billion times larger if it tabulated functions at 15 figure inputs. Instead, it tabulated functions for 4 figure inputs and gives you a recipe (Lagrange interpolation) for evaluating the functions at 15 figure inputs if you desire. This is a very common pattern. An SVG image, for example, does not tell you pixel values, but gives you equations for calculating pixel values at whatever scale is needed.

Related posts

Duct tape value creation

Posted on by John

Excerpt from John Carmack’s review of the book Bullshit Jobs.

He talks about how software developers bemoan duct taping systems together, and would rather work on core technologies. He thinks it is some tragic failure, that if only wise system design was employed, you wouldn’t be doing all the duct taping.

Wrong.

Every expansion in capabilities opens up the opportunity to duct tape it to new areas, and this is where a lot of value creation happens. Eventually, when a sufficient amount of duct tape is found in an area, it is an opportunity for systemic redesigns, but you don’t wait for that before grabbing newly visible low hanging fruit!

The realistic alternative to duct tape and other aesthetically disappointing code is often no code.

Related posts

One-liner to troubleshoot LaTeX references

Posted on by John

In LaTeX, sections are labeled with commands like \label{foo} and referenced like \ref{foo}. Referring to sections by labels rather than hard-coded numbers allows references to automatically update when sections are inserted, deleted, or rearranged.

For every reference there ought to be a label. A label without a corresponding reference is fine, though it might be a mistake. If you have a reference with no corresponding label, and one label without a reference, there’s a good chance the reference is a typo variation on the unreferenced label.

We’ll build up a one-liner for comparing labels and references. We’ll use grep to find patterns that look like labels by searching for label{ followed by any string of letters up to but not including a closing brace. We don’t want the label{ part, just what follows it, so we’ll use look-behind syntax, to exclude it from the match.

Here’s our regular expression:

    (?<=label{)[^}]+

We’re using Perl-style look-behind syntax, so we’ll need to give grep the -P option. Also, we only want the match itself, not matching lines, so we’ll also using the -o option. This will print all the labels:

    grep -oP '(?<=label{)[^}]+' foo.tex

The regex for finding references is the same with label replaced with ref.

To compare the list of labels and the list of references, we’ll use the comm command. For more on comm, see Set theory at the command line.

We could save the labels to a file, save the references to a file, and run comm on the two files. But we’re more interested in the differences between the two lists than the two lists, so we could pass both as streams to comm using the <(...) syntax. Finally, comm assumes its inputs are sorted so we pipe the output of both grep commands to sort.

Here’s our one-liner

    comm -12 <(grep -oP '(?<=label{)[^}]+' foo.tex | sort) 
             <(grep -oP '(?<=ref{)[^}]+' foo.tex | sort)

This will produce three sections of output: labels which are not references, references which not labels, and labels that are also references.

If you just want to see references that don’t refer to a label, give comm the option -13. This suppresses the first and third sections of output, leaving only the second section, references that are not labels.

You can also add a -u option (u for unique) to the calls to sort to suppress multiple instances of the same label or same reference.