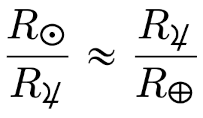When I first started programming I’d occasionally get an error because a delimiter wasn’t matched. Maybe I had a { without a matching }, for example. Or if I were writing Pascal, which I did back in the day, I might have had a BEGIN statement without a corresponding END statement.

At some point I saw someone type an opening delimiter, then the closing delimiter, then back up and insert the content in between. That seemed strange for about five seconds, then I realized it was brilliant and have adopted that practice ever since.

I’ve rarely seen a mismatched delimiter since then, but I ran into one this morning. In order to explain what happened, I’ll need to talk about LaTeX syntax.

LaTeX delimiters

LaTeX has two modes for math symbols: inline and display. Inline symbols appear in the middle of a sentence, while displayed symbols are set apart on their own line and centered. This is analogous to inline elements and block elements in HTML.

When I learned LaTeX, everyone used one dollar sign for inline mode and two dollar signs for display mode. So, for example, you would write $x$ for an x in the context of prose, and $$x = 5$$ to display an equation stating that x equals 5.

Now the preferred syntax is to use \[ to begin display mode and \] to end it. This has several advantages. In particular it makes it easier to debug mismatched delimiter errors since you can count the number of open and closed delimiters; you couldn’t tell without context whether $$ begins or ends a displayed equation.

It’s still common to use dollar signs for inline math mode, but there is an alternate notation that uses \( to begin and \) to end. This notation is not commonly used as far as I know. Escaped parentheses have all the theoretical advantages of escaped brackets, but in practice the scope of inline math content is very small and so it’s not a problem that the opening and closing delimiters are the same.

Org-mode

The only time I use \( and \) is when I’m not directly writing LaTeX but writing an org-mode file that generates LaTeX. I chose to write a client’s repoort in org-mode rather than directly in LaTeX because the document is very long, and so org-mode’s outlining is convenient. I can hide or expand parts of the tree by pressing a tab, for example. Also, the document has a few tables, and tables are easier to write in org-mode’s markdown than in LaTeX.

Unfortunately org-mode sometimes understands expressions like $x$ and sometimes it doesn’t. It would be safer to always write \(x\) but the former works often enough that I tend to use it out of habit. The root of my problem this morning was I had used dollar sign delimiters in a way that confused org-mode.

All else being equal, it’s best when opening and closing delimiters are different. I might advise someone learning LaTeX today to use the \(x\) notation, even though I continue to use $x$.

Chiastic patterns

When I was trying to debug my unmatched delimiter problem, I searched for all \begin and \end statements in my (org-mode generated) LaTeX file by searching on the regular expression \\begin\|\\end. Here’s an example of what I got back (with indentation added).

    \begin{quote}
    \end{quote}
    \begin{table}[htbp]
        \begin{tabular}{ll}
        \end{tabular}
    \end{table}
    \begin{algorithm}
        \begin{algorithmic}[1]
            \begin{enumerate}
            \end{enumerate}
        \end{algorithmic}
    \end{algorithm}

Sometimes opening and closing delimiters are consecutive, such as the beginning and end of the quote. But sometimes you’ll find a chiasmus pattern, named for the Greek letter χ. Notice the table above has an ABBA pattern and the algorithm has an ABCCBA pattern.

This kind of pattern is extremely common in the Bible, though it’s easy for modern readers to miss it. One reason this pattern matters is that the context of a sentence is not only the sentences above and below, but also the parallel sentence in the chiastic pattern. Furthermore, the most important point in a chiasmus is often at the middle.

While chiastic patterns were common in ancient eastern prose, they are far less common in modern western prose. However, chiastic patters are common in programming, so common that no one ever comments on them.

You can see the chiastic pattern in the indentation of source code. The context of a delimiter is its matching delimiter, which may many lines away. And the most important line of code for optimization is the code in the innermost loop, at the focus of a chiasmus.

I became aware of chiastic patterns in the Bible by reading Paul Through Mediterranean Eyes. This book has many outline illustrations that look a lot like source code such as nested for-loops.

Lawyers write Word documents and mathematicians write LaTeX documents. Of course makes collaboration awkward, but there are ways to make it better.

One solution is to simply use Word. People who use LaTeX probably know how to use Word, even if they’d rather not, and asking someone else to learn LaTeX is a non-starter. So if I’m coauthoring a document with a lawyer, I’ll use Word.

If I’m writing a report that a lawyer needs to review, I’ll use LaTeX. Using different programs actually helps because it makes a clear distinction between copy editing feedback and authorial responsibility.

This post will give a couple tips for writing reports in LaTeX to be delivered to a lawyer, one trivial and one not quite trivial.

The trivial tip is that \S produces the section sign § (U+00A7) common in legal documents but not so common elsewhere. The not so trivial tip is that the enumitem package lets you change the default labels that LaTeX uses with enumerated items.

Changing enumerated item labels

LaTeX was designed under the assumption that the user wants to focus on logical structure and leave the formatting up to the typesetting program. Consistent with this design philosophy, nested enumerated lists simply wrapped with \begin{enumerate} and \end{enumerate} and individual list items are marked with \item, regardless of the level of nesting. LaTeX takes responsibility for displaying different labels at different levels: Arabic numerals for top-level lists, Roman letters for the next level of list, etc.

When you’re quoting legal documents, however, you don’t want to simply preserve the logical structure of (nested) lists; you want to preserve the labels as well.

Suppose you have the following nested list.

    \begin{enumerate} 
    \item First top-level item
    \item Second top-level item
      \begin{enumerate}
      \item A sub-item
      \item Another sub-item
        \begin{enumerate}
        \item A third-level item
        \item Another third-level item
          \begin{enumerate}
            \item Four levels in
            \end{enumerate}
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

By default, LaTeX will format this as follows.

But suppose in order to match another document you need the labels to progress as (a), (1), (A), and (i). The following LaTeX code will accomplish this.

    \begin{enumerate} [label={(\alph*)}]
    \item First top-level item
    \item Second top-level item
      \begin{enumerate} [label={(\arabic*)}]
      \item A sub-item
      \item Another sub-item
        \begin{enumerate} [label={(\Alph*)}]
        \item A third-level item
        \item Another third-level item
          \begin{enumerate} [label={(\roman*)}]
            \item Four levels in
            \end{enumerate}      
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

This produces the following.

Note the parentheses in the labels above. You can replace remove one or both, replace them with square brackets, add periods, etc. as the following example shows.

    \begin{enumerate} [label={\alph*)}]
    \item First top-level item
    \item Second top-level item
      \begin{enumerate} [label={\arabic*.}]
      \item A sub-item
      \item Another sub-item
        \begin{enumerate} [label={(\Alph*)}]
        \item A third-level item
        \item Another third-level item
          \begin{enumerate} [label={[\roman*]}]
            \item Four levels in
            \end{enumerate}      
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

Here’s what this looks like when compiled.

Related posts

• Explaining probability to a jury
• Data privacy consulting