I saw something yesterday saying that the Japanese bond market had experienced a six standard deviation move. This brought to mind a post I’d written eight years ago.

All probability statements depend on a model. And if you’re probability model says an event had a probability six standard deviations from the mean, it’s more likely that your model is wrong than that you’ve actually seen something that rare. I expand on this idea here.

How likely is it that a sample from a random variable will be six standard deviations from its mean? If you have in mind a normal (Gaussian) distribution, as most people do, then the probability is on the order of 1 chance in 10,000,000. Six sigma events are not common for any distribution, but they’re not unheard of for distributions with heavy tails.

Let X be a random variable with a Student t distribution and ν degrees of freedom. When ν is small, i.e. no more than 2, the tails of X are so fat that the standard deviation doesn’t exist. As ν → ∞ the Student t distribution approaches the normal distribution. So in some sense this distribution interpolates between fat tails and thin tails.

What is the probability that X takes on a value more than six standard deviations from its mean at 0, i.e. what does the function

f(ν) = Prob(X > 6σ)

look like as a function of ν where σ² = ν/(ν − 2) is the variance of X?

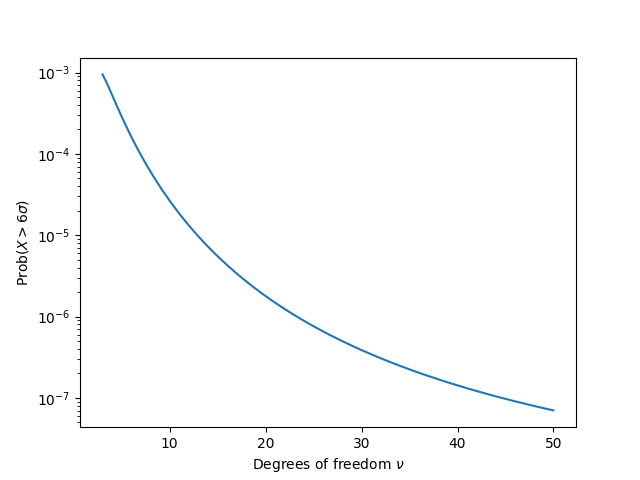
As you’d expect, the limit of f(ν) as ν → ∞ is the probability of a six-sigma event for a normal distribution, around 10⁻⁷ as mentioned above. Here’s a plot of f(ν) for ν > 3. Notice that the vertical axis is on a log scale, i.e. the probability decreases exponentially.

What you might not expect is that f(ν) isn’t monotone. It rises to a maximum value before it decays exponentially. In hindsight this makes sense. As ν → 2⁺ the variance becomes infinite, and the probability of being infinitely far from the mean is 0. Here’s a plot of f(ν) between 2 and 3.

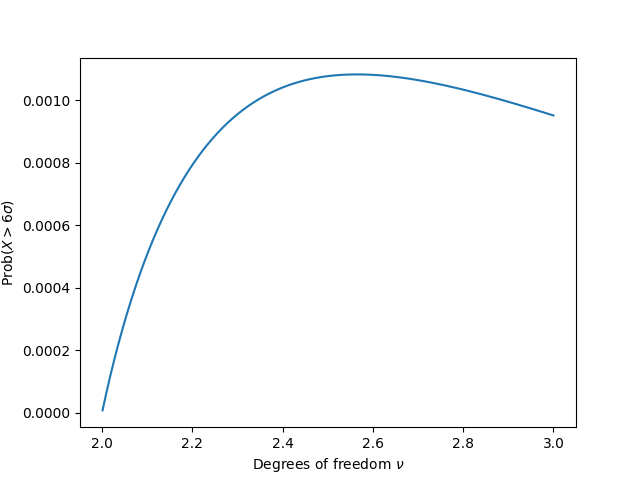
So six sigma probabilities for a Student t distribution rise from 0 up to a maximum of around 10⁻³ then decrease exponentially, then asymptotically approach a value around 10⁻⁷.

Related posts

• Converting between nines and sigmas
• When ν = 30 isn’t normal enough
• Fat tails and the t-test
• Beer, wine, and statistics

The first difficulty in trying to fit an exponential distribution to data is that the data may not follow an exponential distribution. Nothing grows exponentially forever. Eventually growth slows down. The simplest way growth can slow down is to follow a logistic curve, but fitting a logistic curve has its own problems, as detailed in the previous post.

Suppose you are convinced that whatever you’re wanting to model follows an exponential curve, at least over the time scale that you’re interested in. This is easier to fit than a logistic curve. If you take the logarithm of the data, you now have a linear regression problem. Linear regression is numerically well-behaved and has been thoroughly explored.

There is a catch, however. When you extrapolate a linear regression, your uncertainly region flares out as you go from observed data to linear predictions based on the observed data. Your uncertainty grows linearly. But remember that we’re not working with the data per se; we’re working with the logarithm of the data. So on the original scale, the uncertainty flares out exponentially.

One of the more subtle ideas to convey in an introductory statistics class is that statistics have distributions.

Students implicitly think that when you calculate a statistic on a data set, say the mean, that then you have THE mean. But if your data are (modeled as) samples from a random variable, then anything you compute from those samples, such as the mean, is also a random variable. When you compute a useful statistic, it’s not as random as the data, i.e. it has smaller variance, but it’s still random.

A couple days ago I wrote about Fisher’s transform to make the distribution sample correlations closer to normal. This post will make that more concrete.

Preliminaries

We’ll need to bring in a few Python libraries. While we’re at it, let’s set the random number generator seed so the results will be reproducible.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skew

np.random.seed(20251020)

Correlated RNG

Next, we’ll need a way to generate correlated random samples, specifying the correlation ρ and the sample size N.

def gen_correlated_samples(rho, N):
    mean = [0, 0]
    cov = [
        [1, rho],
        [rho, 1]
    ]
    return np.random.multivariate_normal(mean, cov, size=N)

Calculating correlation

Once we generate correlated pairs, we need to calculate their correlation. To be more precise, their linear (Pearson) correlation. To do this we’ll find the empirical covariance matrix, the sample counterpart to the covariance matrix specified in the generator code above. The correlation coefficient is then the off-diagonal element of the covariance matrix.

def pearsonr(X):
    correlation_matrix = np.corrcoef(X[:,0], X[:,1])
    return correlation_matrix[0, 1]

Simulation

Now we’re ready to do our simulation.

M = 10000
rs = np.zeros(M)
for i in range(M):
    X = gen_correlated_samples(0.9, 100)
    rs[i] = pearsonr(X)

Notice that there are two levels of sampling. We’re generating random samples of size 100 and computing their correlation; that’s sampling our underlying data. And we’re repeating the process of computing the correlation 10,000 times; that’s sampling the correlation.

Untransformed distribution

Next we view the distribution of the correlation values.

plt.hist(rs, bins=int(np.sqrt(M)))
plt.show()
plt.close()

This gives the following plot.

It’s strongly skewed to the left, which we can quantify by calculating the skewness.

print(skew(rs))

This tells us the skewness is −0.616. A normal distribution has skewness 0. The negative sign tells us the direction of the skew.

Transformed distribution

Now let’s apply the Fisher transformation and see how it makes the distribution much closer to normal.

xformed = np.arctanh(rs)
plt.hist(xformed, bins=int(np.sqrt(M)))
plt.show()
plt.close()
print(skew(xformed))

This produces the plot below and prints a skewness value of −0.0415.

Small correlation example

We said before that when the correlation ρ is near zero, the Fisher transformation is less necessary. Here’s an example where ρ = 0.1. It’s not visibly different from a normal distribution, and the skewness is −0.1044.

Observation and conjecture

In our two examples, the skewness was approximately −ρ. Was that a coincidence, or does that hold more generally? We can test this with the following code.

def skewness(rho):
    rs = np.zeros(M)
    for i in range(M):
        X = gen_correlated_samples(rho, 100)
        rs[i] = pearsonr(X)
    return skew(rs)
    
rhos = np.linspace(-1, 1, 100)
ks = [skewness(rho) for rho in rhos]
plt.plot(rhos, ks)
plt.plot(rhos, -rhos, "--", color="gray")
plt.show()

Here’s the resulting plot.

It looks like the skewness is not exactly −ρ, but −cρ for some c < 1. Maybe c depends on the inner sample size, in our case 100. But it sure looks like skewness is at least approximately proportional to ρ. Maybe this is a well-known result, but I haven’t seen it before.

Almost Sure posted an interesting fact on X:

If a point (x, y, z) is chosen at random uniformly on the unit sphere, then x, y, and z each have the uniform distribution on [−1, 1] and zero correlations (but not independent!) This follows from Archimedes’ “On the Sphere and Cylinder” published in 225BC.

Archimedes effectively showed that projecting a sphere to a cylinder wrapping round its equator preserves area, so projection of (x,y,z) is uniform on the cylinder. Used in Lambert cylindrical equal area projection.

In this post I want to empirically demonstrate the distribution of the coordinates, their lack of linear correlation, and their dependence.

The usual way to generate random points on a sphere is to generate three samples from a standard normal distribution and normalize by dividing by the Euclidean norm of the three points. So to generate a list of N points on a sphere, I generate an N × 3 matrix of normal samples and divide each row by its norm.

import numpy as np

N = 10000
# Generate N points on a sphere
M = norm.rvs(size=(N, 3))
M /= np.linalg.norm(M, axis=1)[:, np.newaxis]

Next, I find the correlation of each column with the others.

x = M[:, 0]
y = M[:, 1]
z = M[:, 2]
cxy, _ = pearsonr(x, y)
cyz, _ = pearsonr(y, z)
cxz, _ = pearsonr(x, z)
print(cxy, cyz, cxz)

When I ran this I got correlations of -0.0023, 0.0047, and -0.0177. For reasons explained in the previous post, I’d expect values in the interval [−0.02, 0.02] if the columns were independent, so the correlations are consistent with that hypothesis.

To demonstrate that each column is uniformly distributed on [−1, 1] you could look at histograms.

import matplotlib.pyplot as plt

plt.hist(x, bins=int(N**0.5))
plt.show()
plt.hist(y, bins=int(N**0.5))
plt.show()
plt.hist(z, bins=int(N**0.5))
plt.show()

I’ll spare you the plots, but they look like what you’d expect. If you wanted to do something more analytical than visual, you could compute something like the Kolmogorov-Smirnov statistic.

The coordinates are not independent, though they have zero linear correlation. Maybe a test for nonlinear dependence will work. I tried Spearman’s rank correlation and Kendall’s tau, and neither detected the dependence. But distance correlation did.

from dcor import distance_correlation

cxy = distance_correlation(x, y)
cyz = distance_correlation(y, z)
cxz = distance_correlation(x, z)
print(cxy, cyz, cxz)

Each of the distance correlations was approximately 0.11, substantially greater than zero, implying dependence between the coordinates.

Related posts

• Alternative way to generate points on a sphere
• Generate random points inside a sphere
• Approximately evenly spaced points on a sphere