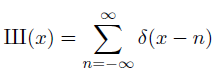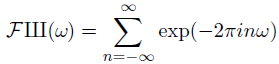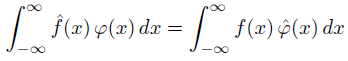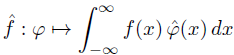Fourier series and Fourier transforms may seem more different than they are because of the way they’re typically taught. Fourier series are presented more as a representation of a function, not a transformation. Here’s a function on an interval. We can write it as a sum of sines and cosines, just as we can write a function as a sum of powers in a power series. There’s not much emphasis on the coefficients per se. They appear inside a sum, but don’t get much attention on their own.

Fourier transforms, on the other hand, are presented as genuine transforms. Here’s a function, and here’s its transform, another function. One’s a function of time, the other a function of frequency. Or maybe both are presented as representations of the same function in two different domains, the time domain and the frequency domain.

You could think of the Fourier series as a kind of transform, taking a periodic function and mapping it to an infinite sequence, the Fourier series coefficients. And you could think of the Fourier transform as being a kind of continuous set of coefficients for representing a function, if you interpret the inversion theorem the right way.

Here are a couple connections between Fourier series and Fourier transforms. Start with a function f on an interval and compute its Fourier series. The Fourier series is periodic, so we could think of f as periodic, even though we only care about f on the interval. Instead, let’s think of extending f to be 0 everywhere outside the interval. Now we take the Fourier transform of f. The Fourier series coefficients are the Fourier transform of f evaluated at integer arguments.

Now let’s go back to thinking of f as a periodic function. What would it’s Fourier transform look like? In classical analysis, you can’t do that. Periodic functions have Fourier series but they don’t have Fourier transforms because the integral defining the latter does not converge. But by the magic of tempered distributions, we can indeed take the Fourier transform of a periodic function. The result is a weighted sum of delta distributions at each integer, and the coefficient of the delta distribution at n is the nth Fourier series coefficient.

The proof of the claim in the previous paragraph is simple once you understand the sha function Ш. Start with a function f defined on a unit interval and extended to be zero outside that interval. Convolving f with Ш make a periodic function f*Ш extending f. The Fourier transform of a convolution is the product of the convolutions. The Fourier transform of f is simply its classical Fourier transform F. The Ш function is its own Fourier transform, so the transform of f*Ш is FШ. Multiplying a function by Ш samples that function, and the samples of F are the Fourier coefficients of the Fourier series of f*Ш, the periodic extension of f.

Here’s an interesting line from Brad Osgood:

Isn’t it a little embarrassing that multibillion dollar industries seem to depend on integrals that don’t converge?

In context, he’s not saying that huge companies are blithely using bad math. Some are, but that’s not what he’s getting at here. His discussion is an example of coming full circle, where experts and novices come to the same conclusion for different reasons.

The divergent integrals Osgood refers to are Fourier transforms of certain functions. A beginner might not notice that said integrals don’t converge. An expert knows that the calculations are justified by a more sophisticated theory. Someone in-between would have objections. Experts can be casual, not because they’re ignorant of technical difficulties but because they’ve mastered these difficulties. [1]

The expert in Fourier analysis has all the technicalities in the back of his or her mind. Often these don’t need to be explicitly exercised. You can blithely go about using formal calculations that aren’t justified by the classical theory.

But the expert doesn’t entirely come full circle, not in the sense of walking in circles in the woods. It’s more like winding around a parking garage, coming back to the same (x, y) location but one level up. Sometimes the expert needs to pull out the technical machinery to avoid an error the beginner could fall into. The theory of tempered distributions, for example, doesn’t justify every calculation a novice might try.

***

[1] In a nutshell, here’s the theory that justifies apparently sloppy calculations with Fourier transforms. The key is to view the function you want to transform not as a function on the real line but as a tempered distribution, a linear functional on the space of smooth, rapidly decaying test functions. A function acts on a test function by forming their product and integrating. Then use Parseval’s theorem from the classical theory as the definition in this new context, moving the transform operation from the original function to the test function. Simple, right?

The sha function, also known as the Dirac comb, is denoted with the Cyrillic letter sha (Ш, U+0428). This letter was chosen because it looks like how people visualize the function, a long series of vertical spikes. The function is called the Dirac comb for the same reason. This function is very important in Fourier analysis because it relates Fourier series and Fourier transforms. It relates sampling and periodization.  It’s its own Fourier transform, and with a few qualifiers discussed later, the only such function.

The Ш function, really the Ш distribution, is defined as

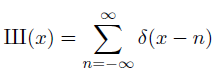
Here δ(x – n) is the Dirac delta distribution centered at n. The action of δ(x – n) on a test function is to evaluate that function at n. You can envision Ш as an infinite sequence of spikes, one at each integer. The action of Ш on a test function is to add up its values at every integer.

Sampling

The product of Ш with a function f is a new distribution whose action on a test function φ is the sum of f φ over all integers. Or you could think of the distribution as a sort of clothesline on which to hang the sampled values of f, much the way a generating function works.

Periodizing

Next let’s look at a function f that lives on [0, 1], i.e. is zero everywhere outside the unit interval. The convolution of f with δ(x – n) is f(x – n), i.e. a copy of f shifted over to live on the interval [n, n+1]. So by taking the convolution with Ш, we create copies of f all over the real line. We’ve made f into a periodic function. So instead of saying “the function f extended to create a periodic function” you can simply say f*Ш.

Fourier transform

Now let’s think about the Fourier transform of Ш. The Fourier transform of δ(x) is 1, i.e. the function equal to 1 everywhere [1].  (The more concentrated a function is, the more spread out its Fourier transform. So if you have an infinitely concentrated function δ, its Fourier transform is perfectly flat, 1. You can calculate the transform rigorously, this is the intuition.) If you shift a function by n, you rotate its Fourier transform by exp(-2πinω). So we can compute the transform of Ш:

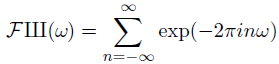
This equation only makes sense in terms of distributions. The right hand side does not converge in the classical sense; the individual terms don’t even go to zero, since each term has magnitude 1. So what kind of distribution is this thing on the right side? It is in fact the Ш function again, though this is not obvious.

To see that the exponential sum is actually the Ш function, i.e. that Ш is its own Fourier transform, we need to back up a little bit and define Fourier transform of a distribution. As usual with distributions, we take a classical theorem and turn it into a definition in a broader context.

For absolutely integrable functions, we have

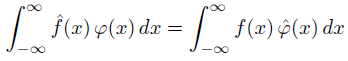
where the hat on top of a function indicates its Fourier transform. Inspired by the theorem above, we define the Fourier transform of a distribution f to be the functional whose action on a test function φ is given below.

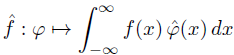
As we noted in a previous post, the integral above can be taken literally if f is a distribution associated with an ordinary function, but in general it means the application of the linear functional to the test function.

As a distribution, exp(-2πinω) acts on a test function φ by integrating against it. From the definition of a (classical) Fourier transform, this gives the Fourier transform of φ evaluated at n. So the Fourier transform of Ш acts on φ by summing the values of φ’s Fourier transform over all integers. By the Poisson summation formula, this is the same as summing the values of φ itself over all integers. Which is the same as applying Ш. So the Fourier transform of Ш has the same effect on test functions as Ш. In other words, Ш is its own Fourier transform.

Uniqueness

We haven’t been explicit about where our test functions come from. We require that xⁿ φ(x) goes to zero as x goes to ±∞ for any positive integer n. These are called functions of rapid decay. And the distributions we define as linear functionals on such test functions are called tempered distributions.

The Ш distribution is essentially unique. Any tempered distribution with period 1 that equals its own Fourier transform must be a multiple of Ш.

***

[1] All Fourier transform calculations here use the convention I call (-1, τ, 1) in these notes on various definitions. This may be the most common definition, though there are several minor variations in common use.

In the previous post, we looked at an elegant equation involving integrals of the sinc function and computed the corresponding integrals for the jinc function.

It turns out the analogous equation holds for sums as well:

As before, we’d like to compute these two sums and see whether we can compute the corresponding sums for the jinc function.

The Poisson summation formula says that a function and its Fourier transform produce the same sums over the integers:

Recall from the previous post that the Fourier transform of sinc is the function π box(π x) where the box function is 1 on [-1/2, 1/2] and zero elsewhere. The only integer n with πn inside [-1/2, 1/2] is 0, so the sum of sinc(n) over the integers equals π. A very similar argument shows that the sum of jinc(n) over the integers equals its Fourier transform at 0, which equals 2.

Let tri(x) be the triangle function, defined to be 1 – |x| for -1 < x < 1 and 0 otherwise. Then the Fourier transform of tri(x) is sinc²(π ω) and so π tri(π x) and sinc² are Fourier transform pairs. The Poisson summation formula says the sum of sinc² over the integers is the sum of π tri(π x) over the integers, which is π.

I don’t know the Fourier transform of jinc² and doubt it’s easy to compute. Maybe the sum could be computed more easily without Fourier transforms, e.g. using contour integration.

The sinc function is defined by sinc(x) = sin(x)/x. Philip Woodward introduced the name of the function in 1952, saying it “occurs so often in Fourier analysis and its applications that it does seem to merit some notation of its own.”

Here’s an elegant equation involving the integrals of the sinc function:

When I ran across this recently I wondered two things: How hard is it to compute these two integrals? What are the corresponding results for the jinc function? The jinc function is analogous to sinc, but using a Bessel function in place of sine: jinc(x) = J₁(x)/x.

The Fourier transform of the box function, the function box(x) that is 1 on the interval [-1/2, 1/2] and zero everywhere else, is sinc(π ω). (That’s one of the reasons sinc comes up so often in Fourier analysis, as Woodward observed.) So the Fourier transform of sinc(x) is π box(π x). The integral of a function is the value of its Fourier transform at zero, so sinc integrates to π. [1]

By Plancherel’s theorem, the integral of sinc²(x) is the integral of its Fourier transform squared, which equals π.

[There are several conventions for defining the Fourier transform. Here I’m using what I call the (-1, τ, 1) definition in these notes. See that page for other conventions and how to convert between them.]

Now for the jinc function. It also has a simple Fourier transform: f(ω) = 2 √(1 – (2πω)) for |x| < 1/2π and zero otherwise. As above, we can compute the integral of jinc over the real line by evaluating its Fourier transform at 0, which equals 2.

Also as above, the integral of jinc² is the integral of its Fourier transform squared, which works out to 8/3π.

Update: See the next post for the analogous relations for sums.

More on sinc and jinc functions

• Jinc function
• How to compute the jinc function
• Area of sinc and jinc lobes

[1] You may have a couple objections to this calculation. I found the Fourier transform of the box function was sinc, then concluded that the transform of sinc is the box function. But applying the Fourier transform twice doesn’t give you the original function back, right? When you transform f(x) twice you get  f(-x), but the functions involved here are even, so  f(-x) =  f(x).

OK, but you may still have another objection: the sinc function does not have bounded L¹ norm, so you can’t just take its Fourier transform. True, but you can justify the transform in terms of L² theory or distribution theory.