Interesting post from Brendan O’Connor:
Comparison of data analysis packages: R, Matlab, SciPy, Excel, SAS, SPSS, Stata
Rstats
Better R console fonts
The default installation of R on Windows uses Courier New for the console font. Unfortunately, this font offers low contrast between the letter ‘l’ and the number ‘1.’ There is also poor contrast between the letter ‘O’ and the number ‘0.’ The contrast between period and commas is OK.
Lucida Console is an improvement. It has high contrast between ‘l’ and ‘1’, though ‘O’ and ‘0’ are still hard to distinguish. But my favorite console font is Consolas. It offers strong contrast between ‘l’ and ‘1’, commas and periods, and especially between lower case ‘o’, upper case ‘O’, and the number ‘0.’
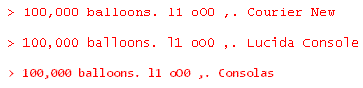
Consolas is more legible while also fitting more characters into the same horizontal space. It can do this because it uses ClearType anti-aliasing while the other two fonts do not. Here is a sample of the three fonts magnified 4x to show the anti-aliasing.
I found setting the default console font in R a little tricky. Clicking on the Edit -> GUI preferences menu brings up the Rgui Configuration Editor. From there it’s obvious how to change the font. However, what I found surprising is that clicking the “OK” button only changes the font for the current session. I can’t think of another application that behaves analogously. To set your choice of font for all future sessions, click “Save” rather than “OK.”
* * *
R, Excel, and the Windows clipboard
The Windows version of R has functions for reading from and writing to the clipboard. These can be used to move data back and forth between R and Windows applications such as Excel. However, there are a few gotchas. See the following link for details.
Five kinds of subscripts in R
Five kinds of things can be subscripts in R, and they all behave differently.
- Positive integers
- Negative integers
- Zero
- Booleans
- Nothing
For all examples below, let x be the vector (3, 1, 4, 1, 5, 9).
Positive integers
Ordinary vector subscripts in R start with 1, like FORTRAN and unlike C and its descendants. So for the vector above, x[1] is 3, x[2] is 1, etc. R doesn’t actually have scalar types; everything is a vector, so subscripts are vectors. In the expression x[2], the subscript is a vector containing a single element equal to 2. But you could use the vector (2, 3) as a subscript of x, and you’d get (1, 4).
Negative integers
Although subscripts that reference particular elements are positive, negative subscripts are legal. However, they may not do what you’d expect. In scripting languages, it is conventional for negative subscripts to indicate indexing from the end of the array. So in Python or Perl, for example, the statement y = x[-1] would set y equal to 9 and y = x[-2] would set y equal to 5.
In R, a negative is an instruction to remove an element from a vector. So y = x[-2] would set y equal to the vector (3, 4, 1, 5, 9), i.e. the vector x with the element x[2] removed.
While R’s use of negative subscripts is unconventional, it makes sense in context. In some ways vectors in R are more like sets than arrays. Removing elements is probably a more common task than iterating backward.
Zero
So if positive subscripts index elements, and negative subscripts remove elements, what does a zero subscript do? Nothing. It doesn’t even produce an error. It is silently ignored. See Radford Neal’s blog post about zero subscripts in R for examples of how bad this can be.
Booleans
Boolean subscripts are very handy, but look very strange to the uninitiated. Ask a C programmer to guess what x[x>3] would be and I doubt they would have an idea. A Boolean expression with a vector evaluates to a vector of Boolean values, the results of evaluating the expression componentwise. So for our value of x, the expression x>3 evaluates to the vector (FALSE, FALSE, TRUE, FALSE, TRUE, TRUE). When you use a Boolean array as a subscript, the result is the subset of elements whose index corresponds to an index in the Boolean array containing a TRUE value. So x[x>3] is the subset of x consisting of elements larger than 3, i.e. x[x>3] equals (4, 5, 9).
When a vector with a Boolean subscript appears in an assignment, the assignment applies to the elements that would have been extracted if there had been no assignment. For example, x[x > 3] <- 7 turns (3, 1, 4, 1, 5, 9) into (3, 1, 7, 1, 7, 7). Also, x[x > 3] <- c(10, 11, 12) would produce (3, 1, 10, 1, 11, 12).
Nothing
A subscript can be left out entirely. So x[] would simply return x. In multi-dimensional arrays, missing subscripts are interpreted as wildcards. For example, M[3,] would return the third row of the matrix M.
Mixtures
Fortunately, mixing positive and negative values in a single subscript array is illegal. But you can, for example, mix zeros and positive numbers. And since numbers can be NA, you can even include NA as a component of a subscript.
Related resources
Default arguments and lazy evaluation in R
In C++, default function arguments must be constants, but in R they can be much more general. For example, consider this R function definition.
f <- function(a, b=log(a)) { a*b }
If f is called with two arguments, it returns their product. If f is called with one argument, the second argument defaults to the logarithm of the first. That’s convenient, but it gets more surprising. Look at this variation.
f <- function(a, b=c) {c = log(a); a*b}
Now the default argument is a variable that doesn’t exist until the body of the function executes! If f is called with one argument, the R interpreter chugs along until it gets to the last line of the function and says “Hmm. What is b? Let me go back and see. Oh, the default value of b is c, and now I know what c is.”
This behavior is called lazy evaluation. Expressions are not evaluated unless and until they are needed. It’s a common feature of functional programming languages.
There’s a little bit of lazy evaluation in many languages: the second argument of a Boolean expression is often not evaluated if the expression value is determined by the first argument. For example, the function bar() in the expression
while (foo() && bar())
will not be called if the function foo() returns false. But functional languages like R take lazy evaluation much further.
R was influenced by Scheme, though you could use R for a long time without noticing its functional roots. That speaks well of the language. Many people find functional programming too hard and will not use languages that beat you over the head with their functional flavor. But it’s intriguing to know that the functional capabilities are there in case they’re needed.
Related resources
R programming coming from other languages
The R programming language is fairly easy to learn once you get in the right mindset, but until you get in that mindset the language is bewildering. If you come to R from any popular programming language, you’re in for a number of surprises. I recently revised some notes I first posted about a year ago to help programmers coming to R from other languages.
Distributions in Mathematica and R/S-PLUS
I posted some notes this evening on working with probability distributions in Mathematica and R/S-PLUS.
I much prefer Mathematica’s syntax. The first time I had to read some R code I ran across a statement something like runif(1, 3, 4). I thought it was some sort of conditional execution statement: run something if some condition holds. No, the code generates a random value uniformly from the interval (3, 4). The corresponding Mathematica syntax is Random[ UniformDistribution[3,4] ].
Another example. The statement pnorm(x, m, s) in R corresponds to PDF[ NormalDistribution[m, s], x ] in Mathematica. Both evaluate the PDF of a normal random variable with mean m and standard deviation s at the point x.
It’s a matter of taste. Some people prefer terse notation, especially for things they use frequently. I’d rather type more and remember less.
Preventing an unpleasant Sweave surprise
Sweave is a tool for making statistical analyses more reproducible by using literate programming in statistics. Sweave embeds R code inside LaTeX and replaces the code with the result of running the code, much like web development languages such as PHP embed code inside HTML.
Sweave is often launched from an interactive R session, but this can defeat the whole purpose of the tool. When you run Sweave this way, the Sweave document inherits the session’s state. Here’s why that’s a bad idea.
Say you’re interactively tinkering with some plots to make them look like you want. As you go, you’re copying R code into an Sweave file. When you’re done, you run Sweave on your file, compile the resulting LaTeX document, and get beautiful output. You congratulate yourself on having gone to the effort to put all your R code in an Sweave file so that it will be self-contained and reproducible. You forget about your project then revisit it six months later. You run Sweave and to your chagrin it doesn’t work. What happened? What might have happened is that your Sweave file depended on a variable that wasn’t defined in the file itself but happened to be defined in your R session. When you open up R months later and run Sweave, that variable may be missing. Or worse, you happen to have a variable in your session with the right name that now has some unrelated value.
I recommend always running Sweave from a batch file. On Windows you can save the following two lines to a file, say sw.bat, and process a file foo.Rnw with the command sw foo.
R.exe -e "Sweave('%1.Rnw')"
pdflatex.exe %1.tex
This assumes R.exe and pdflatex.exe are in your path. If they are not, you could either add them to your path or put their full paths in the batch file.
Running Sweave from a clean session does not insure that your file is self-contained. There could still be other implicit dependencies. But running from a clean session improves the chances that someone else will be able to reproduce the results.
See Troubleshooting Sweave for some suggestions for how to prevent or recover from other possible problems with Sweave.
Update: See the links provided by Gregor Gorjanc in the first comment below for related batch files and bash scripts.
* * *
Literate programming and statistics
Sweave, mentioned in my previous post, is a tool for literate programming. Donald Knuth invented literate programming and gives this description of the technique in his book by the same name:
I believe that the time is ripe for significantly better documentation of programs, and that we can best achieve this by considering programs to be works of literature. Hence, my title: “Literate Programming.”
Let us change our traditional attitude to the construction of programs: Instead of imagining that our main task is to instruct a computer what to do, let us concentrate rather on explaining to human beings what we want a computer to do.
The practitioner of literate programming can be regarded as an essayist, whose main concern is with exposition and excellence of style. Such an author, with thesaurus in hand, chooses the names of variables carefully and explains what each variable means. He or she strives for a program that is comprehensible because its concepts have been introduced in an order that is best for human understanding, using a mixture of formal and informal methods that reinforce each other.
Knuth says the quality of his code when up dramatically when he started using literate programming. When he published the source code for TeX as a literate program and a book, he was so confident in the quality of the code that he offered cash rewards for bug reports, doubling the amount of the reward with each edition. In one edition, he goes so far as to say “I believe that the final bug in TeX was discovered and removed on November 27, 1985.” Even though TeX is a large program, this was not an idle boast. A few errors were discovered after 1985, but only after generations of Stanford students studied the source code carefully and multitudes of users around the world put TeX through its paces.
While literate programming is a fantastic idea, it has failed to gain a substantial following. And yet Sweave might catch on even though literate programming in general has not.
In most software development, documentation is an after thought. When push comes to shove, developers are rewarded for putting buttons on a screen, not for writing documentation. Software documentation can be extremely valuable, but it’s most valuable to someone other than the author. And the benefit of the documentation may only be realized years after it was written.
But statisticians are rewarded for writing documents. In a statistical analysis, the document is the deliverable. The benefits of literate programming for a statistician are more personal and more immediate. Statistical analyses are often re-run, with just enough time between runs for the previous work to be completely flushed from term memory. Data is corrected or augmented, papers come back from review with requests for changes, etc. Statisticians have more self-interest in making their work reproducible than do programmers.
Patrick McPhee gives this analysis for why literate programming has not caught on.
Without wanting to be elitist, the thing that will prevent literate programming from becoming a mainstream method is that it requires thought and discipline. The mainstream is established by people who want fast results while using roughly the same methods that everyone else seems to be using, and literate programming is never going to have that kind of appeal. This doesn’t take away from its usefulness as an approach.
But statisticians are more free to make individual technology choices than programmers are. Programmers typically work in large teams and have to use the same tools as their colleagues. Statisticians often work alone. And since they deliver documents rather than code, statisticians are free to use Sweave without their colleagues’ knowledge or consent. I doubt whether a large portion of statisticians will ever be attracted to literate programming, but technological minorities can thrive more easily in statistics than in mainstream software development.
Irreproducible analysis
Journals and granting agencies are prodding scientists to make their data public. Once the data is public, other scientists can verify the conclusions. Or at least that’s how it’s supposed to work. In practice, it can be extremely difficult or impossible to reproduce someone else’s results. I’m not talking here about reproducing experiments, but simply reproducing the statistical analysis of experiments.
It’s understandable that many experiments are not practical to reproduce: the replicator needs the same resources as the original experimenter, and so expensive experiments are seldom reproduced. But in principle the analysis of an experiment’s data should be repeatable by anyone with a computer. And yet this is very often not possible.
Published analyses of complex data sets, such as microarray experiments, are seldom exactly reproducible. Authors inevitably leave out some detail of how they got their numbers. In a complex analysis, it’s difficult to remember everything that was done. And even if authors were meticulous to document every step of the analysis, journals do not want to publish such great detail. Often an article provides enough clues that a persistent statistician can approximately reproduce the conclusions. But sometimes the analysis is opaque or just plain wrong.
I attended a talk yesterday where Keith Baggerly explained the extraordinary steps he and his colleagues went through in an attempt to reproduce the results in a medical article published last year by Potti et al. He called this process “forensic bioinformatics,” attempting to reconstruct the process that lead to the published conclusions. He showed how he could reproduce parts of the results in the article in question by, among other things, reversing the labels on some of the groups. (For details, see “Microarrays: retracing steps” by Kevin Coombes, Jing Wang, and Keith Baggerly in Nature Medicine, November 2007, pp 1276-1277.)
While they were able to reverse-engineer many of the mistakes in the paper, some remain a mystery. In any case, they claim that the results of the paper are just wrong. They conclude “The idea … is exciting. Our analysis, however, suggests that it did not work here.”
The authors of the original article replied that there were a few errors but that these have been fixed and they didn’t effect the conclusions anyway. Baggerly and his colleagues disagree. So is this just a standoff with two sides pointing fingers at each other saying the other guys are wrong? No. There’s an important asymmetry between the two sides: the original analysis is opaque but the critical analysis is transparent. Baggerly and company have written code to carry out every tiny step of their analysis and made the Sweave code available for anyone to download. In other words, they didn’t just publish their paper, they published code to write their paper.
Sweave is a program that lets authors mix prose (LaTeX) with code (R) in a single file. Users do not directly paste numbers and graphs into a paper. Instead, they embed the code to produce the numbers and graphs, and Sweave replaces the code with the results of running the code. (Sweave embeds R inside LaTeX the way CGI embeds Perl inside HTML.) Sweave doesn’t guarantee reproducibility, but it is a first step.