“For a list of all the ways technology has failed to improve the quality of life, please press 3.” — Alice Kahn
Month: November 2009
A case for robust Bayesian priors
A paper I wrote with Jairo Fúquene and Luis Pericchi is now available online.
A Case for Robust Bayesian Priors with Applications to Clinical Trials
Jairo Fúquene, John Cook, and Luis Pericchi
Bayesian Analysis (2009) 4, Number 4, pp. 817–846.
Travels with Charley
Over the Thanksgiving break I read Travels with Charley, John Steinbeck’s book about his trip across America in 1961 with his French poodle Charley. I had been interested in reading the book since I saw it quoted in Dave Gibson’s blog this summer.
Steinbeck explains in the preface why he chose to go on his trip.
During the previous winter I had become rather seriously ill with one of those carefully named difficulties which are the whispers of approaching age. … And I had seen so many [older men] begin to pack their lives in cotton wool, smother their impulses, hood their passions, and gradually retire from their manhood into a kind of spiritual and physical semi-invalidism. In this they are encouraged by wives, and relatives, and it’s such a sweet trap. Who doesn’t want to be the center for concern? … I knew that in ten or twelve thousand miles driving a truck, alone and unattended, over every kind of road, would be hard work, but to me it represented the antidote for the poison of the professional sick man. … If this projected journey should prove too much then it was time to go anyway.
Travels with Charley is filled with insightful observations of ordinary people Steinbeck met along the way.There was even one brief mention of a mathematician.
The dairy man had a Ph. D. in mathematics, and he must have had some training in philosophy. He liked what he was doing and he didn’t want to be somewhere else — one of the very few contented people I met in my whole journey.
Maybe I should buy a dairy.
One of my favorite descriptions is of a man that Steinbeck didn’t meet in person: Steinbeck gives an account of the life of a man by the evidence left behind in a hotel room.
I enjoyed Travels with Charley until Steinbeck and Charley made it to the West Coast. Steinbeck’s description of his return trip is not nearly as enjoyable to read. The end of the book has fewer descriptions of people and more commentary. Steinbeck becomes tedious. He is looking forward to end his trip, and so are his readers. I recommend Travels with Charley, but I also recommend stopping after they see the giant redwoods.

A beta-like distribution
I just stumbled across a distribution that approximates the beta distribution but is easier to work with in some ways. It’s called the Kumaraswamy distribution. Apparently it came out of hydrology. The graph below plots the density of the distribution for various parameters. If you’re familiar with the beta distribution, these curves will look very familiar.
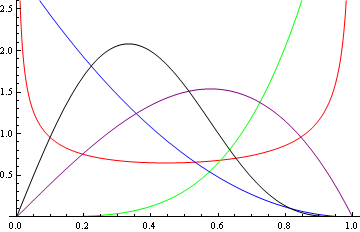
The PDF for the Kumaraswamy distribution K(a, b) is
f(x | a, b) = abxa-1(1 – xa)b-1
and the CDF is
F(x | a, b) = 1 – (1 – xa)b.
The most convenient feature of the Kumaraswamy distribution is that its CDF has a simple form. (The CDF for a beta distribution cannot be reduced to elementary functions unless its parameters are integers.) Also, the CDF is easy to invert. That means you can generate a random sample from a K(a, b) distribution by first generating a uniform random value u and then returning
F-1(u) = (1 – (1 – u)1/b)1/a.
If you’re going to use a Kumaraswamy distribution to approximate a beta distribution, the question immediately arises of how to find parameters to get a good approximation. That is, if you have a beta(α, β) distribution that you want to approximate with a K(a, b) distribution, how do you pick a and b?
My first thought was to match moments. That is, pick a and b so that K(a, b) has the same mean and variance as beta(α, β). That may work well, but it would have to be done numerically.
Since the beta(α, β) density is proportional to xα (1-x)β-1 and the K(a, b) distribution is proportional to xa(1 – xa)b, it seems reasonable to set a = α. But how do you pick b? The modes of the two distributions have simple forms and so you could pick b to match modes:
mode K(a, b) = ((a – 1)/(ab – 1))1/a = mode beta(α, β) = (α – 1)/(α + β – 2).
Update: I experimented with the method above, and it’s OK, but not great. Here’s an example comparing a beta(1/2, 1/2) density with a K(1/2, 2 – √2) density.
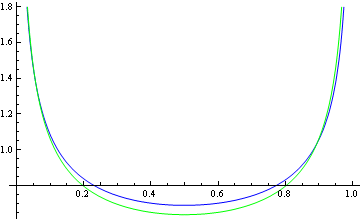
Here the K density matches the beta density not at the mode but at the minimum. The blue curve, the curve on top, is the beta density.
Here’s another example, this time comparing a beta(5, 3) density and a K(5, 251/40) density.
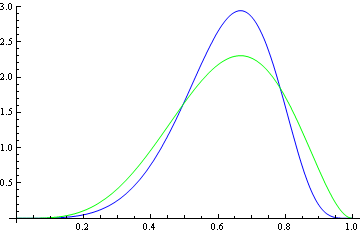
Again the beta density is the blue curve, on top at the mode.
Maybe the algorithm I suggested for picking parameters is not very good, but I suspect the optimal parameters are not much better. Rather than saying that the Kumaraswamy distribution approximates the beta distribution, I’d say that the Kumaraswamy distribution is capable of assuming roughly the same shapes as the beta distribution. If the only reason you’re using a beta distribution is to get a certain density shape, the Kumaraswamy distribution would be a reasonable alternative. But if you need to approximate a beta distribution closely, it may not work well enough.
Thomas Edison’s fire
When Thomas Edison was sixty-seven years old, his factory was destroyed in a fire. This was his response the next morning:
There’s value in disaster. All our mistakes are burned up. Thank God, we can start anew.
Related posts
It doesn’t pay to be the computer guy
This weekend I ran across a post by Shaun Boyd called Ten reasons it doesn’t pay to be the computer guy [link has gone away]. He begins with the observation that if you’re “the computer guy,” most of your accomplishments are invisible. Nobody consciously notices things working smoothly. In fact, if you do a great job of preventing problems, people will assume you’re not needed. After discussing being unappreciated, Boyd goes on to complain about unreasonably high expectations people have of “the computer guy.”
These are valid complaints. However, they somewhat offset each other. Yes, much computer support work is invisible, but the firefighting aspects of the job are very visible and often appreciated. Other computer careers are less visible than desktop support and do not have the same potential for positive client interaction. Security may be the worst. Nobody ever notices the lack of security problems. The only potential visibility is negative.
I think the problem is not so much a lack of visibility but a natural incentive to concentrate on the more visible aspects of the job. It’s natural to do more of what is rewarded and less of what is ignored. Troubleshooting is often immediately rewarded by the gratitude of clients. (“My computer was all messed up and you saved me. Thank you, computer guy!”) Preventative maintenance and infrastructure improvements are appreciated only in the long term, if ever.
These challenges are not unique to computer careers; cure is usually more appreciated than prevention. The other problems Boyd lists are not unique to computer careers either. For example, he mentions the lack of appreciation for specialization.
There is no common understanding that there are smaller divisions within the computer industry, and that the computer guy cannot be an expert in all areas.
Every industry has its specializations, though specializations within the computer industry may be less widely known. Maybe specializations are harder to appreciate in newer industries; not long ago the computer guy could be an expert in more areas. Another difficulty is that computers are mysterious to most people. They find it easier to imagine why there are different kinds of doctors for eyes and ears than why there are different kinds of computer guys for desktops and servers.
Boyd makes one point that is almost unique to the computer industry: rapid change devalues skills. Every industry experiences change, but few change at the same rate as the computer industry.
Thanks to the constantly declining price of new computers, the computer guy cannot charge labor sums without a dispute. … desktop computers are always getting smaller, faster, and cheaper. It’s possible to purchase a new desktop computer for under $400. If the computer guy spends five hours fixing a computer and wants $100/hour for his time, his customer will be outraged, exclaiming “I didn’t even spend this much to BUY the computer, why should I pay this much just to FIX it?”
When people in other professions complain about how their jobs are changing, they’re usually complaining directly or indirectly about the impact of computer technology. But the rate of change for those who use a technology is usually less than the rate of change for those who produce and support it.
Related posts
Tragedy of the anti-commons
The tragedy of the commons is the name economists use to describe the abuse of common property. For example, overfishing in international waters. Someone who owns a lake will not over fish his own lake because he knows he will benefit in the future from restraining his fishing now. But in international waters, no individual has an incentive to restrain fishing. Mankind as a whole certainly benefits from restraint, but single fishermen do not.
Michael Heller discusses an opposite effect, the tragedy of the anti-commons, on the EconTalk podcast. The tragedy of the commons describes the over-use of a resource nobody owns. The tragedy of the anti-commons describes the under-use of resources with many owners. For example, suppose an acre of land belongs to 43,560 individuals who each own one square foot. The land will never be used for anything as long as thousands of people have to agree on what to do.
The example of land being divided into tiny plots is a artificial. A more realistic example is the ownership of patents. Building a DVD player requires using hundreds of patented inventions. No company could ever build a DVD player if it had to negotiate with all patent holders and obtain their unanimous consent. These patents would be worthless due to gridlock. Fortunately, the owners of the patents used in building DVD players have formed a single entity authorized to negotiate on their behalf. But if you’re creating something new that does not have an organized group of patent holders, there are real problems.
According to Michael Heller, it is simply impossible to create a high-tech product these days without infringing on patents. A new drug or a new electronic device may use thousands of patents. It may not be practical even to discover all the possible patents involved, and it is certainly not possible to negotiate with thousands of patent holders individually.
Small companies can get away with patent violations because the companies may not be worth suing. But companies with deep pockets such as Microsoft are worth suing. These companies develop their own arsenal of patents so they can threaten counter suits against potential attackers. This keeps the big companies from suing each other, but it doesn’t prevent lawsuits from tiny companies that may only have one product.
Listen to the EconTalk interview for some ideas of how to get around the tragedy of the anti-commons, particularly in regard to patents.
Random inequalities IX: new tech report
Just posted: Exact calculation of inequality probabilities. This report summarizes previous results for calculating P(X > Y) where X and Y are random variables.
Previous posts on random inequalities:
Three quotes on software development
Here are three quotes on software development I ran across yesterday.
From Douglas Crockford, author of JavaScript, The Good Parts:
Just because something is a standard it doesn’t mean it’s the right choice for every application (e.g. XML).
From Yukihiro Matsumoto, creator of Ruby:
An open source project is like a shark. It must keep moving, or it will die.
From Roger Sessions, CTO of ObjectWatch:
A good IT architecture is made up largely of agreements to disagree. … Bad architectures and good both contain disagreements, but the bad architectures lack agreements on how to do so.
I once worked on a project that had a proprietary file format that became more sophisticated over time until it resembled a primitive relational database. After that I resolved to use standard technologies as much as possible. I think others have had the same experience and overreacted, using standard technologies even when they are overkill. Crockford’s comment is a reminder to moderate one’s zeal for standards. Moderation in all things.
I would add to Matsumoto’s comment that it’s not only open source projects that need to keep moving or die, though they may have an extra need for movement to maintain credibility. (Update: See this post on how software, networks, and storage all have to keep moving to survive.)
The way I understand Sessions’ comment is that good architecture focuses on high level agreement rather than low-level conformity. “Let’s rewrite all our code in Java” is not a good software architecture. Or one that I hear more often “Let’s move everything to Oracle.” Such low-level standardization does not guarantee a coherently organized system. Whether subsystems use the same implementation technologies is not as important as whether there is a good strategy for making the pieces fit together.
Related posts
Office 2007 documents are zipped XML
Microsoft Office 2007 documents are zipped XML files. For example, you can change a Word document’s extension from .docx to .zip and unzip it. Apparently this isn’t widely known; most people I talk to are surprised when I mention this.
I’ve found a couple uses for the zip/XML format. One is that you can unzip a document and grab all the embedded content. For example, .jpeg images are simply files that are zipped up into the Office document.
Another use is that you can crack open a document’s underlying XML to search for something you can’t find via the user interface. You can unzip Office documents, tweak them, and zip them back up. I don’t recommend this, but I’ve done it when I was desperate. (Microsoft publishes an API for manipulating Office files. Using the official APIs is safer and in the long run easier, but I haven’t looked into it.)
