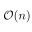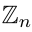When I solve a problem by appealing to symmetry, students’ jaws drop. They look at me as if I’d pulled a rabbit out of a hat.
I used think of these tricks as common knowledge, but now I think they’re common knowledge in some circles (e.g. physics) and not as common in others. These tricks are simple, but not as many people as I’d thought have been trained to spot opportunities to apply them.
Here’s an example.
Pop quiz 1: Evaluate the following intimidating integral.
Solution: Zero, by symmetry, because the integrand is odd.
The integrand is an odd function (i.e. f(−x) = −f(x)), and the integrand of an odd function over a symmetric interval is zero. This is because the region below the x-axis is symmetric to the region above the x-axis as the following graph shows.
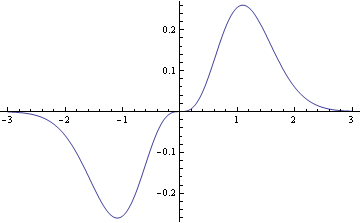
The example above is not artificial: similar calculations come up constantly in applications. For example, the Fourier series of an odd function contains only sine terms, no cosine terms. Why? The integrals to compute the Fourier coefficients for the cosine terms all involve odd functions integrated over an interval symmetric about zero.
Another common application of symmetry is evaluating derivatives. The derivative of an odd function is an even function and vice versa.
Pop quiz 2: What is the coefficient of x5 in the Taylor series of cos(1 + x2)?
Solution: Zero, by symmetry, because cos(1 + x2) is an even function.
Odd functions of x have only odd powers of x in their Taylor series and even functions have only even powers of x in their Taylor series. Why? Because the coefficients come from derivatives evaluated at zero.
If f(x) is an odd function, all of its even derivatives are odd functions. These derivatives are zero at x = 0, and so all the coefficients of even powers of x are zero. A similar argument shows that even functions have only even powers of x in their Taylor series.
Symmetry tricks are obvious in hindsight. The hard part is learning to recognize when they apply. Symmetries are harder to recognize, but also more valuable, in complex situations. The key is to think about the problem you’re trying to solve before you dive into heads-down calculation.