There are now over 100,000 followers across my various daily tip Twitter accounts. The three most popular are CompSciFact, AlgebraFact, and ProbFact. The newest account GrokEM has the least followers for now.
Thank you everyone for following and for providing feedback.
Sometimes a graph looks wiggly because it’s actually quite flat.
This isn’t much of a paradox; the resolution is quite simple. A graph may look wiggly because the scale is wrong. If the graph is flat, graphing software may automatically choose narrow vertical range, accentuating noise in the graph. I haven’t heard a name for this, though I imagine someone has given it a name.
Here’s an extreme example. The following graph was produced by the Mathematica command Plot[Gamma[x+1] - x Gamma[x], {x, 0, 1}].
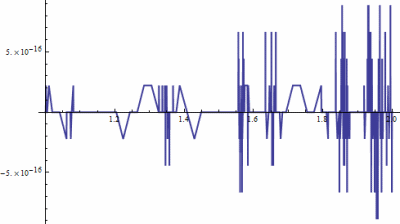
This is unsettling the first time you run into it, until you notice the vertical scale. In theory, Γ(x + 1) and x Γ(x) are exactly equal. In practice, a computer returns slightly different values for the two functions for some arguments. The differences are on the order of 10-15, the limit of floating point precision. Mathematica looks at the range of the function being plotted and picks the default vertical scaling accordingly.
In the example above, the vertical scale is 15 orders of magnitude smaller than the horizontal scale. The line is smooth as glass. Actually, it’s much smoother than glass. An angstrom is only 10 orders of magnitude smaller than a meter, so you wouldn’t have to look at glass under nearly as much magnification before you see individual atoms. At a much grosser scale you’d see imperfections in the glass.
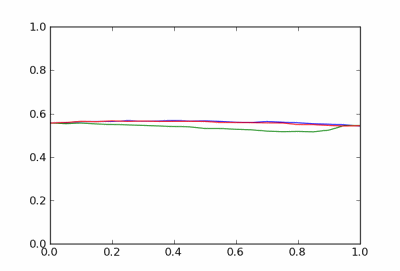
The graph above is so jagged that it demands our attention. When the horizontal axis is closer to the proper scale, say off by a factor of 5 or 10, the problem can be more subtle. Here’s an example that I ran across yesterday.
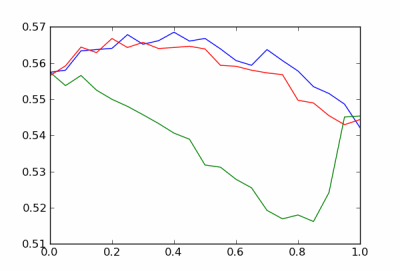
The curves look awfully jagged, but this is just simulation noise. The function values are probabilities, and when viewed on a scale of probabilities the curves look unremarkable.
From The First Circle by Alexander Solzhenitsyn:
Now listen to the rule of the last inch. The realm of the last inch. The job is almost finished, the goal almost attained, everything possible seems to have been achieved, every difficulty overcome — and yet the quality is just not there. The work needs more finish, perhaps further research. In that moment of weariness and self-satisfaction, the temptation is greatest to give up, not to strive for the peak of quality. That’s the realm of the last inch — here, the work is very, very complex, but it’s also particularly valuable because it’s done with the most perfect means. The rule of the last inch is simply this — not to leave it undone. And not to put it off — because otherwise your mind loses touch with that realm. And not to mind how much time you spend on it, because the aim is not to finish the job quickly, but to reach perfection.
Via Still I Am One
It can be hard to know when something deserves the kind of polish Solzhenitsyn talks about. Sometimes you’re in the realm of rapidly diminishing return and it’s time to move on. Other times, the finishing touches are everything.
Related post: Scripting and the last mile problem
Last week I wrote about how memoization reduced a simulation’s execution time from 300 hours down to 38 minutes. This weekend I came up with a different approach that reduces the time down to 21 minutes by taking advantage of a recurrence relation.
The most expensive function in the simulation has four integer arguments. Each time the function is called, one of the arguments is incremented by 1. A random process determines which argument is incremented each time. This function has a set of recurrence relations that make it faster to calculate a new value if you have a previously computed value for adjacent arguments.
The recurrence relation approach is about 100x faster than the memoization approach for small runs. However, the time per run with memoization decreases with each run. The longer it runs, the more values it caches, and so the greater the chances that a value has already been computed. In the end, the recurrence relation is about 2x faster than the memoization approach. With an even larger run, I suspect the time for the two approaches would be roughly equal.
The new approach is faster, but it was more work to implement, and it depends critically on the assumption that consecutive arguments differ only by one increment of one argument.
Related post: 20 weeks down to 20 minutes
I had a simulation this week that I estimated would take 20 weeks to run. This estimate was based on too small a run. A more reliable estimate based on a longer run was 300 CPU hours, about two weeks running on a single processor. Before I split the problem up to run in parallel, I wanted to see if I could make each thread run faster.
The most expensive part of the simulation is a function that takes in four integer parameters and does a numerical integration. Each parameter could be any value from 0 to 120. So in principle there are 1214 = 214,358,881 possible parameter combinations. I knew that some of these combinations were extremely unlikely or impossible, so I thought I could reduce the execution time by caching the most commonly called parameters. Maybe a few thousand arguments would account for most of the function calls.
I saved the function arguments and computed values in map, a.k.a. dictionary, associative array, etc. (The buzz word for this is memoization.) I set a maximum size on the map because I thought it could grow very large. Even if, say, a thousand arguments accounted for most of the function calls, maybe there were many more that only appeared once.
It turned out that the function was only called with 408 distinct parameter combinations. That means the same integrals were being evaluated millions of times. Caching these values reduced the execution time by a factor of about 800. In other words, the software could retrieve a previously computed value 800x faster than compute it from scratch.
The simulation that would have taken 300 hours took only 22 minutes, and so there was no need to make it run in parallel.
Update: I found a bug in my hashing algorithm. After fixing the bug, the time to run my simulations increased to 38 minutes. So my speed-up was a about a factor of 420 rather than 800, but still enough to run on one thread over lunch. The number of distinct arguments to the numerical integration was much more than 408 in the corrected program, but still small enough to cache.
In The Linux Command Line, the author describes the bash man page* as “the most brutal man page of them all.”
Many man pages are hard to read, but I think that the grand prize for difficulty has to go to the man page for
bash. As I was doing my research for this book, I gave it a careful review to ensure that I was covering most of its topics. When printed, it’s over 80 pages long and extremely dense, and its structure makes absolutely no sense to a new user.On the other hand, it is very accurate and concise, as well as being extremely complete. So check it out if you dare, and look forward to the day when you can read it and it all makes sense.
* If you’re not familiar with Unix lingo, “man” stands for “manual”. Man pages are online documentation.
Related post: Review of The Linux Command Line
No Starch Press recently released The Linux Command Line: A Complete Introduction (ISBN 1593273894) by William E. Shotts, Jr.
True to its name, the book is about using Linux from command line. It’s not an encyclopedia of Linux. It doesn’t explain how to install Linux, doesn’t go into system APIs, and says little about how to administer Linux. At the same time, the book is broader than just a book on bash. It’s about how to “live” at the command line.
The introduction explains the intended audience.
This book is for Linux users who have migrated from other platforms. Most likely you are a “power user” of some version of Microsoft Windows.
The book has a conversational style, explaining the motivation behind ways of working as well as providing technical detail. It includes small but very useful suggestions along the way, the kinds of tips you’d pick up from a friend but might not find in a book.
The book has four parts
The book could have just included the first three sections; the forth part is a bit more specialized than the others. If you’d prefer, think of the book has having three parts, plus a lengthy appendix on shell scripting.
The Linux Command Line is pleasant to read. It has a light tone, while also getting down to business.
Related post:
Perverse hipster desire for retro-computing
This is the most encouraging thing I’ve seen in cancer research in some time: a way to make tumors fluoresce. This allows surgeons to see tumor boundaries.
From TED (link rotted)
What we call “differential equations” are usually not just differential equations. They also have associated initial conditions or boundary conditions.
With ordinary differential equations (ODEs), the initial conditions are often an afterthought. First you find a full set of solutions, then you plug in initial conditions to get a specific solution.
Partial differential equations (PDEs) have boundary conditions (and maybe initial conditions too). Since people typically learn ODEs first, they come to PDEs expecting boundary values to play a role analogous to ODEs. In a very limited sense they do, but in general boundary values are quite different.
The hard part about PDEs is not the PDEs themselves; the hard part is the boundary conditions. Finding solutions to differential equations in the interior of a domain is easy compared to making the equations have the specified behavior on the boundary.
No model can take everything into account. You have to draw some box around that part of the world that you’re going to model and specify what happens when your imaginary box meets the rest of the universe. That’s the hard part.
Universities are starting to give away their content online, while they still charge tens of thousands of dollars a year to attend. Just what are they selling? Credentials, accountability, and feedback.
Some people are asking why go to college when you can download a college education via iTunes U.
First, you would have no credentials when you’re done.
Second, you almost certainly would not put in the same amount of work as a college student without someone to pace you through the material and to provide external motivation. You’d be less likely to struggle through anything you found difficult or uninteresting.
Third, you’d have no feedback to know whether you’re really learning what you think you’re learning.
The people that I hear gush about online education opportunities are well-educated, successful, and ambitious. They may be less concerned about credentials either because they are intrinsically motivated or because they already have enough credentials. And because of their ambition, they need less accountability. They may need less feedback or are resourceful enough to seek out alternative channels for feedback, such as online forums. Resources such iTunes U and The Teaching Company are a godsend to such people. But that doesn’t mean that a typical teenager would make as much of the same opportunities.
