Uncategorized

Golden convergence

Posted on by John

The golden ratio φ satisfies the following equation.

\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}}

The proof most commonly given is to let x equal the right-hand side of the equation, then observe that x² = 1 + x, the quadratic equation for the golden ratio. The quadratic has two roots: φ and −1/φ. Since x > 1, x = φ.

This proof tacitly assumes that the expression above is meaningfully defined, and then manipulates it algebraically. But is it meaningfully defined? What exactly does the infinitely nested sequence of radicals mean?

You could interpret the nested radicals to be the limit of the iteration

x \mapsto \sqrt{1 + x}

and show that the limit exists.

What should the starting value of our iteration be? It seems natural to choose x = 1, but other values will do. More on that shortly. We could compute φ by implementing the iteration in Python as follows.

    x_old, x_new = 0, 1
    while (abs(x_old - x_new) > 1e-15):
        x_new, x_old = (1 + x_new)**0.5, x_new
    print(x_new)

The program terminates, so the iteration must converge, right? Probably so, but that’s not a proof. To be more rigorous, define

f(x) = \sqrt{1 + x}

and so

f^\prime(x) = \frac{1}{2\sqrt{1 + x}}

This shows 0 < f ′(x) < ½ for any positive x and so the function f(x) is a contraction mapping. This means the iterations converge. We could start with any x > −¾ and the derivative would still be less than 1, so the iterations would converge.

We can visualize the process of convergence starting with x = 0 using the following cobweb plot.

Related posts

Mnemonic images with Grok 3

Posted on by John

The Major mnemonic system makes numbers easier to memorize by encoding them as words. Each digit corresponds to one or more consonant sounds, and you can fill in vowels as you wish.

In August 2022 I tried creating a few images using DALL-E 2. The results were disappointing and sometimes disturbing.

To illustrate the use of the Major system, I gave the example of memorizing a list of the US presidents by creating mental images associating each president with the number of their term as president. For example, Franklin Delano Roosevelt was the 32nd POTUS. You can encode 32 as “moon”, so you might imagine FDR looking up at the moon.

At the time, Grover Cleveland was the only US President to serve two non-consecutive terms, being both the 22nd and 24th president. I asked DALL-E to create an image of Grover the Muppet holding an onion (22) and a wiener dog (24). This was too much for DALL-E at the time. The image below was as close as I could get.

Blue dog holding cucumber dog?

When I asked Grok 3 for a similar image it did a much better job. To be fair, it initially put a different dog breed in Grover’s hand, but I asked it to change the dog to a dachshund and it performed admirably.

Grover holding an onion and a wiener dog

Related posts

Russian Morse Code

Posted on by John

I read something once about an American telegraph operator who had to switch over to using Russian Morse code during WWII. I wondered how hard that would be, but let it go. The idea came back to me and I decided to settle it.

It would be hard to switch from being able to recognize English words to being able to recognize Russian words, but that’s not the the telegrapher had to do. He had to switch from receiving code groups made of English letters to ones made of Russian letters.

Switching from receiving encrypted English to encrypted Russian is an easier task than switching from English plaintext to Russian plaintext. Code groups were transmitted at a slower speed than words because you can never learn to recognize entire code groups. Also, every letter of a code group is important; you cannot fill in anything from context.

Russian Morse code consists largely of the same sequences of dots and dashes as English Morse code, with some additions. For example, the Russian letter Д is transmitted in Morse code as -.. just like the English letter D. So our telegraph operator could hear -.. and transcribe it as D, then later change D to Д.

The Russian alphabet has 33 letters so it needs Morse codes for 7 more letters than English. Actually, it uses 6 more symbols, transmitting Е and Ё with the same code. Some of the additional codes might have been familiar to our telegrapher. For example Я is transmitted as .-.- which is the same code an American telegrapher would use for ä (if he bothered to distinguish ä from a).

All the additional codes used in Russian correspond to uncommon Latin symbols (ö, ch, ñ, é, ü, and ä) and so our telegrapher could transcribe Russian Morse code without using any Latin letters.

The next question is how the Russian Morse code symbols correspond to the English. Sometimes the correspondence is natural. For example, Д is the same consonant sound as D. But the correspondence between Я and ä is arbitrary.

I wrote about entering Russian letters in Vim a few weeks ago, and I wondered how the mapping of Russian letters to English letters implicit in Morse code corresponds to the mapping used in Vim.

Most Russian letters can be entered in Vim by typing Ctrl-k followed by the corresponding English letter and an equal sign. The question is whether Morse code and Vim have the same idea of what corresponds to what. Many are the same. For example, both agree that Д corresponds to D. But there are some exceptions.

Here’s the complete comparison.

     Vim   Morse
А    A=    A
Б    B=    B
В    V=    W
Г    G=    G
Д    D=    D
Е    E=    E
Ё    IO    E
Ж    Z%    V
З    Z=    Z
И    I=    I
Й    J=    J
К    K=    K
Л    L=    L
М    M=    M
Н    N=    N
О    O=    O
П    P=    P
Р    R=    R
С    S=    S
Т    T=    T
У    U=    U
Ф    F=    F
Х    H=    H
Ц    C=    C
Ч    C%    ö
Ш    S%    ch
Щ    Sc    Q
Ъ    ="    ñ
Ы    Y=    Y
Ь    %"    X
Э    JE    é
Ю    JU    ü
Я    JA    ä

Related posts

Chebyshev and Russian transliteration

Posted on by John

It’s not simple to transliterate Russian names to English. Sometimes there is a unique mapping, or at least a standard mapping, of a particular name, but often there is not.

An example that comes up frequently in mathematics is Pafnuty Lvovich Chebyshev (1821–1894). This Russian mathematician’s name Пафну́тий Льво́вич Чебышёв has been transliterated at Tchebichef, Tchebychev, Tchebycheff, Tschebyschev, Tschebyschef, Tschebyscheff, Čebyčev, Čebyšev, Chebysheff, Chebychov, Chebyshov, etc.

The American Mathematical Society has settled on “Chebyshev” as its standard, and this is now common in English mathematical writing. But things named after Chebyshev, such as Chebyshev polynomials, are often denoted with a T because the French prefer “Tchebyshev.”

There is an ISO standard, ISO 9, for transliterating Cyrillic characters into Latin characters. Under this standard, Чебышёв becomes Čebyšëv. This maps Cyrillic into Latin characters with diacritical marks but not into ASCII. The AMS realized that the vast majority of Americans would not type Čebyšëv into a search bar, for example, and chose Chebyshev instead.

Related posts

Podcast feed

Posted on by John

The previous post was an AI-generated podcast that I friend made by crawling my web site. I decided to create an actual podcast for posting occasional audio files. I expect to post very sporadically. I’ve posted two audio files, and I have one more in mind to post some day. Maybe that’ll be the end of it, or maybe I’ll post more.

The first file I posted was the one from the previous post. The second was an interview I did with the late Sir Michael Atiyah.

Here’s the RSS feed for the podcast. You can also find the podcast via my Substack newsletter.

Unicode Steganography

Posted on by John

Steganography attempts to prevent messages from being read by unintended recipients by hiding the messages rather than (or in addition to) encrypting them. Steganography is used when you not only want to keep your communication private, you want to hide the fact that you’ve communicated at all.

Fun fact: The words steganography and stegosaurus are related [1].

Famous example

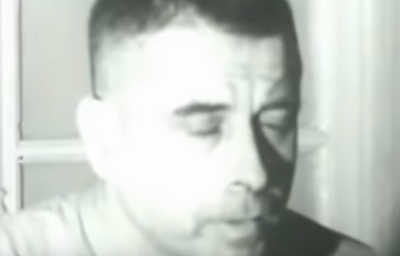
A famous example of steganography was a secret message sent by Jeremiah Denton during the Vietnam War. While a prisoner of war, Denton was forced to participate in a Vietnamese propaganda video. He send the word torture by blinking the Morse code for the letters in the word. You can find the video here.

Clip from Jeremiah Denton propaganda video with Morse code blinking

Famous non-example

Some alleged examples of steganography have turned out to be apophenia, looking for patterns where they do not exist. The book The Woman Who Smashed Codes details Elizebeth Smith’s introduction to cryptography, being tasked to find messages hidden in minor variations in Shakespeare’s handwriting that were not there. The book goes on to describe her cryptographic work during WWII, deciphering messages that most certainly did exist.

Incidentally, Elizebeth Smith [2] married fellow cryptographer William F. Friedman. I wrote about Friedman’s index of coincidence a while back.

Enter Unicode

Randall Monroe said “I am endlessly delighted by the hopeless task that the Unicode Consortium has created for themselves.” One of the things that makes their task delightful and hopeless is trying to distinguish semantics from appearance.

For example, the capital letters  at the beginning of the Roman and Greek alphabets have different Unicode values even though they both look like alike. A (U+0041) is a Roman letter and Α (U+0391) is a Greek letter and so they’re not the same. Also, the Roman letter M (U+004D) is semantically different from the Roman numeral Ⅿ (U+216F) that represents 1,000.

But it quickly becomes impossible to consistently make such distinctions, and so Unicode is full of compromises. Should the letter i and the imaginary unit i have different code points? What about the symbol i for current and the unit basis vector i? You can’t have a different code point for every use of a symbol.

Because Unicode has numerous pairs of characters with identical appearance, it’s possible to hide binary data in Unicode text by using one member of a pair to represent a 0 and the other to represent a 1. So maybe d (U+0064 Latin Small Letter D) represents a 0 and ԁ (U+0501 Cyrillic Small Letter Komi De) represents a 1.

There is a potential problem with this scheme. Unicode does not dictate appearance, and it’s entirely possible a typographer might create a font that has distinct glyphs for characters that are not distinct in other fonts.

Security

Look-alike characters are often used to create malicious URLs. For instance, someone might take “Microsoft.com” and substitute the Roman numeral Ⅿ for the first letter, or substitute a Greek omicron for one of the o‘s.

Text that is expected to ASCII should be turned into ASCII to prevent mistakes or malice, or the user warned. “Do you really want to visit this URL that contains nine Roman letters and one Cyrillic letter?”

When I’m reading, I want fonts with broad Unicode support. No missing symbols, no jarring change in font for foreign words. But when I’m debugging, it would be nice to have the opposite, a xenophobic font that displays non-ASCII characters in some ugly way that makes them jump out. I imagine someone has developed such a font, but it’s hard to find because most people are looking for better Unicode support, not worse.

Related posts

[1] Both derive from the Greek word for ‘cover’. Steganographic writing is covered in the sense of being hidden. A stegosaurus has armored plates that look like roof tiles, i.e. like the covering of a house.

[2] That’s not a typo. She spelled her name with ‘e’ as the fifth letter rather than the more common ‘a’.

Cycle of New Year’s Days

Posted on by John

Here’s a visualization of how the day of the week for New Year’s Day changes.

The green diamonds represent leap years and the blue squares represent ordinary years.

The day of the week for New Year’s Day advances one day after each ordinary year and two days after each leap year, hence the diagonal stripes in the graph above.

The whole cycle repeats every 28 years. During that 28 year cycle, New Year’s Day falls on each day of the week four times: three times in an ordinary year and once in a leap year. Or to put it another way, each horizontal row of the graph above contains three blue squares and one green diamond.

The comments above are true under the Julian calendar, without exception. And they’re true for long stretches of time under the Gregorian calendar. For example, the pattern above repeats from 1901 to 2099.

The Julian calendar had a leap day every four years, period. This made the calendar year longer than the solar year by about 3 days every 400 years, so the Gregorian calendar removed 3 leap days. A year divisible by 100 is not a leap year unless it is also divisible by 400. So the Gregorian calendar disrupts the pattern above every 100 years.

Related posts

Most popular posts of 2024

Posted on by John

I looked at Hacker News to see which posts on this site were most popular. I didn’t look at my server logs, but generally the posts that get the most traffic are posts that someone submits to Hacker News.

Older posts popular this year

Two posts written earlier got a lot of traffic this year, namely

Writes large correct programs

from 2008 and

Where has all the productivity gone?

from 2021.

Posts written this year

The most popular post this year, at least on Hacker News, was

Why does FM sound better than AM?

The runner up was

Evaluating a class of infinite sums in closed form

The following post looks at a way for a satellite to move from one orbit to another that under some circumstances is more efficient (in terms of fuel, not in terms of time) than the more common Hohmann transfer maneuver.

Efficiently transferring to a much higher orbit

This post considers interpolation as a form of compression. Instead of saving a table of function values at fine-grained intervals, you could store values at points further apart and store interpolation formulas for recovering the lost precision.

Compression and interpolation

One of the arguments between Frequentist and Bayesian statisticians is whether you should be allowed to look at data as it accrues during an experiment, such as in A/B testing. If you do look at the interim data, how should you analyze it and how should you interpret the results?

Can you look at experimental results along the way or not?

Finally, I wrote a post about solving a problem I ran into with the command line utility find. As is often the case, I got a lot of useful feedback.

Resolving a mysterious problem with find

 

Putting a face on a faceless account

Posted on by John

I’ve been playing around with Grok today, logging into some of my X accounts and trying out the prompt “Draw an image of me based on my posts.” [1] In most cases Grok returned a graphic, but sometimes it would respond with a text description. In the latter case asking for a photorealistic image made it produce a graphic.

Here’s what I get for @AlgebraFact:

The icons for all my accounts are cerulean blue dots with a symbol in the middle. Usually Grok picks up on the color, as above. With @AnalysisFact, it dropped a big blue piece of a circle on the image.

For @UnixToolTip it kept the & from the &> in the icon. Generative AI typically does weird things with text in images, but it picked up “awk” correctly.

Here’s @ProbFact. Grok seems to think it’s a baseball statistics account.

Last but not least, here’s @DataSciFact.

I wrote a popular post about how to put Santa hats on top of symbols in LaTeX, and that post must have had an outsided influence on the image Grok created.

[1] Apparently if you’re logging into account A and ask it to draw B, the image will be heavily influence by A‘s posts, not B‘s. You have to log into B and ask in the first person.

Perpetual Calendars

Posted on by John

The previous post explained why the Gregorian calendar is the way it is, and that it consists of a whole number of weeks. It follows that the Gregorian calendar repeats itself every 400 years. For example, the calendar for 2025 will be exactly the same as the calendar for 1625 and 2425.

There are only 14 possible printed calendars, if you don’t print the year on the calendar. There are seven possibilities for the day of the week for New Year’s Day, and there are two possibilities for whether the year is a leap year.

A perpetual calendar is a set of the 14 possible calendars, along with some index that tells which possible calendar is appropriate in a given year.

Are each of the 14 calendars equally frequent? Almost, aside from the fact that leap years are less frequent. Each ordinary year calendar occurs 43 or 44 times, and each leap year calendar occurs 13, 14, or 15 times.

Related posts