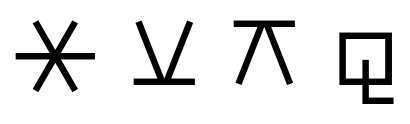I was working recently with a gigabyte file that had a dozen non-ASCII characters. This is very common. The ASCII character set is not quite big enough for a lot of tasks. Of course it’s completely inadequate if you’re writing Japanese, but it’s almost enough for documents written in English and a few other languages.
Efficient encoding
The world has standardized on Unicode as the way to represent characters across languages. Unicode currently has around 150,000 characters, far more than ASCII’s 128 characters.
But there’s a problem. Since 150,000 > 217, it takes more than two bytes (eight bits to a byte) to represent each of 150,000 things. If you use three bytes to represent each character, every file that is almost all ASCII will get three times bigger. If you limit yourself to the most frequently used Unicode characters, those that can be represented with two bytes (the “basic multilingual plane”), then you still double the size of files.
Enter UTF-8, a brilliant solution to this problem. The UTF-8 encoding of an ASCII file is an ASCII file. Pure ASCII files don’t get any larger when interpreted as UTF-8 encoded Unicode. Because 128 = 27, a byte representing an ASCII character has one unused bit. UTF-8 uses this unused bit to signal that what follows is not ASCII. I wrote about the full details here.
Unicode characters outside the ASCII range take 2, 3, or 4 bytes to represent. Inserting a small number of non-ASCII characters into a UTF-8 encoded Unicode file hardly changes the file’s size.
Troubleshooting
I mentioned at the top that I had a gigabyte file with a dozen non-ASCII characters. The command file -I reported the file encoding to be ASCII, because the vast majority of the file was ASCII. But the non-ASCII characters were not valid Unicode characters either.
These invalid Unicode characters would display as �, which is not actually in the file. The � is a valid Unicode character for representing an invalid Unicode character.
Some of the non-ASCII characters where extended ASCII (Windows 1252) characters, but if I remember correctly even that didn’t account for everything. Some of the odd characters were simply file corruption.
It’s kinda interesting how some tools are robust to these kinds of glitches and some are not. My first clue that something funny was going on was when sort refused to sort. I ran a Python script that helps me fix wonky text files and it threw an error:
UnicodeDecodeError: 'utf-8' codec can't decode byte 0x92 in position 222662: invalid start byte
This may seem like gibberish, but it actually says exactly what’s going on. There was an error interpreting the file as Unicode, because 0x92 is not a valid way to start a non-ASCII character in UTF-8.
The first bit of an ASCII character is 0. The first two bits of a non-ASCII character in UTF-8 are 11. But 9 is 1001 in binary, i.e. it starts with 10, and so the byte 0x92 is neither an ASCII character nor the beginning of a UTF-8 non-ASCII sequence of bytes. More details here.
Removing non-ASCII characters
For my application I could just remove the invalid characters using iconv with the -c option.
iconv -c -f CP1252 -t UTF-8 inputfile > outputfile
If you need to salvage troublesome characters then things are a little more complicated. The iconv utility will work if you know what the intended encoding was. If you don’t the intended encoding, you may need to do some detective work.