On the day Apollo 11 left for the moon, Wernher von Braun said “You give me 10 billion dollars and a 10 years and I’ll have a man on Mars.” Perhaps he could have solved the rocketry problem in time and under budget, but the biggest obstacles to visiting Mars are not rocket science. The biggest obstacle may be psychology. How do you keep a crew from sane all the way to Mars and back? Or politics: How do you stir up sufficient public interest in the project without a cold war? Or biology: How would astronauts handle years of exposure to cosmic radiation?
Month: November 2010
New Twitter account: CompSciFact
Next week I’m starting @CompSciFact. This Twitter account will post one fact from computer science per day, Monday through Friday. I’ll also have a few unscheduled posts from time to time. (I announced @StatFact earlier today. There are no more announcements coming! I don’t plan to start any more Twitter accounts any time soon.)
The account may change over time in response to your feedback, but what I have in mind for now is keeping the scheduled facts theoretical: analysis of algorithms, grammars, computability, etc. The unscheduled posts may be less theoretical but at least somewhat related to computer science.
I’m using a “big-Oh” symbol as the image for CompSciFact since a big part of computer science is determining the asymptotic order of the runtime of an algorithm.
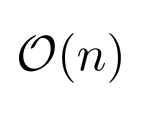
I have several other daily tip accounts. @RegexTip and @TeXtip are the ones most closely related to computer science. I also have several mathematical accounts: @AlgebraFact, @AnalysisFact, @ProbFact, @TopologyFact, and also starting next week, @StatFact. For more details about these accounts, please see the FAQ.
New Twitter account: StatFact
I’m starting a new daily tip account on Twitter. @StatFact will post one statement from statistics per day, drawing from Bayesian and frequentist statistics. Like my other daily tip accounts, StatFact will post Monday through Friday on a regular schedule with a few unscheduled tweets sprinkled in occasionally.
I’m using a product sign as the symbol for StatFact.
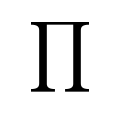
I thought the product sign might suggest a likelihood function. The most obvious symbol for a statistics account would be a bell curve, but that’s been overused.
If you’re interested in StatFact, here are some things you could do.
- Follow StatFact on Twitter.
- Tell friends about StatFact.
- Suggest topics, or even better, specific tweets.
- Propose a better icon.
- Let me know if I say anything ambiguous or wrong.
To find out about my other daily tip accounts, please see the FAQ post.
Where to wait for an elevator

Imagine a bank of three elevators along a wall. The elevators are in a straight line but they are not evenly spaced. Where do you stand in order to minimize the expected distance you’ll need to walk to catch the first elevator that arrives?
This scenario comes from the opening paragraph of a paper by James Handley et al.
If asked where they would stand and wait for the next of three elevators, unequally spaced along a wall, many students would choose to stand at the mean position. They think that by doing so they are minimizing the average distance to the elevator. They do not recognize that standing at the mean minimizes the average squared distance and that the minimal average distance to the elevator is in fact achieved by standing at the median.
Suppose you start out standing in front of the second elevator. If you move one foot to the left, you decrease the distance to first elevator by a foot, but you increase the distance to the other two elevators by one foot as each, so your average distance increases. Similarly, if you move one foot to the right, you decrease your distance to the third elevator but increase your distance to the other two so that you increase the average distance. Since you can’t move without increasing the average distance, you must have started at the best spot.
So standing in front of the second elevator minimizes the expected distance to the next elevator, assuming all three elevators are equally likely to arrive next.
What if you want to minimize the worst case instead of the average case? Stand half way between the first and third elevators. As before, you can see that if you were to move from that position, you’d increase your distance to at least one elevator and thus increase the maximum distance.
This problem illustrates three optimization theorems:
- The sample mean minimizes the total squared distance to a set of points.
- The sample median minimizes the mean absolute distance to a set of points.
- The mid-range minimizes the maximum distance to a set of points.
These theorems have numerous applications. For example, they are foundational in the study of robust estimators.
Links
Apollo 11 wasn’t perfect
The mission that first landed men on the moon could easily have been aborted. From Rocket Men:
Though Apollo 11 is commonly believed to have been a perfect mission, so many things in fact went wrong Kennedy Space Center directory Jay Honeycutt later admitted, “I tell you, it would have been damn easy to abort that mission. Damn easy.”
Related posts
Ruby, Python, and Science
David Jacobs has written a long blog post Ruby is beautiful (but I’m moving to Python). [Update: link no longer available.] Here’s my summary.
Ruby is much better than Java, but the Ruby community is too focused on web development and the language has no scientific library. Python has a lot of the same advantages as Ruby, is used for more than web programming, and has SciPy.
Update: There is now a fledgling SciRuby project.
Further reading
Fairy dust on the diploma
When I was in college, a friend of mine gave me a math book that I found hard to get through. When I complained about it, he told me “You’re going to finish a PhD someday. When you do, do you think there’s going to be fairy dust on the diploma that’s going to enable you to do anything you can’t do now?”
That conversation stuck with me. I realized that I just needed to work hard rather than wait for my intelligence to mysteriously rise at graduation.
Lisp and the anti-Lisp
Doug Hoyte’s book Let Over Lambda is refreshingly opinionated. I don’t share the author’s opinions, but I appreciate his conviction. Hoyte is a zealous advocate for Lisp, and yet he admires Perl as a sort of anti-Lisp. He even calls Perl “beautiful” as far as non-Lisp languages go.
Hoyte argues that Lisp is the greatest programming language because its minimal (i.e. practically non-existent) syntax makes Lisp macro programming powerful. But if you’re going to have language syntax that prevents this style of programming, you might as well go for broke and have lots and lots of syntax.
If we have to have [non-Lisp] syntax — eliminating the possibility of macros — we may as well extend it as far as possible. Let’s throw in all the possible conveniences and power-user tricks we can think of. If Lisp is the result of taking syntax away, Perl is the result of taking syntax all the way.
I understand that Lisp’s lack of syntax opens interesting possibilities. I also understand the advantages of a rich syntax—provided you (and everyone you work with) have mastered the language and use it frequently enough to keep it loaded in your head. However, I prefer a moderate amount of syntax, somewhere between Lisp and Perl, though I admit this may simply be because that’s what I am accustomed to.
Related post: Periodic table of Perl operators
Prestige, value, and satisfaction
Seth Roberts and Daniel Lemire have both written blog posts on prestige. Roberts argues that high-prestige work almost necessarily has low practical value. Lemire takes this idea further and explains why high-prestige work can be unsatisfying.
Related posts
Two kinds of generalization
From George Pólya:
There are two kinds of generalizations. One is cheap and the other is valuable. It is easy to generalize by diluting a little idea with a big terminology. It is much more difficult to prepare a refined and condensed extract from several good ingredients.
Related post: Jenga mathematics
