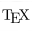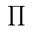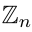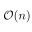RegexTip, a Twitter account for learning regular expressions, starts over today with basics and will progress to more advanced properties over time.
SansMouse, an account for Windows keyboard shortcuts, started over with basics two weeks ago.
Both RegexTip and SansMouse are in a loop, progressing from most basic to more advanced features. (Or perhaps I should say progressing from most familiar to less familiar. Calling some features “basic” and others “advanced” isn’t quite right, especially for keyboard shortcuts.)
The other daily tip accounts don’t post in any particular sequence. I try to alternate elementary and advanced content to some extent, but other than that there’s no order.
Six weeks ago I started two new accounts: CompSciFact and StatFact. In a few days CompSciFact will be the most popular of the daily tip accounts if the current trend continues.
Here are all the accounts:
I use Hoot Suite to schedule these accounts. I use the paid version because I have too many accounts for the free version and because the paid version has an API that lets me upload files to schedule tips in bulk. (Hoot Suite has an affiliate program, so I make a little money if you sign up through this link.)
If you have suggestions for tweets, please contact me.