The slang “tl;dr” stands for “too long; didn’t read.” The context is often either a bad joke or a shallow understanding. What bothers me most about tl;dr is the mindset it implies, scanning everything but reading nothing. I find myself…
Monthly Archives: March 2012
How Emacs influenced Ruby
Ruby creator Yukihiro Matsumoto gave a presentation How Emacs changed my Life in which he explains how Emacs influenced him personally and how it influenced the programming language he created. Here is his summary: Emacs taught me freedom for software.…
Numerous studies have confirmed …
I was listening to a business book in my car this afternoon. A couple times it said Numerous studies have confirmed … and I couldn’t help but hear Several of my peers, who share my prejudices, were also able to…
Polynomial determined by two inputs
Suppose p(x) is a polynomial with integer coefficients. If all the coefficients are non-negative, I can tell you what p(x) is if you’ll tell me the value of p(x) at just two points. This sounds too good to be true.…
Photo quiz: What's this?
What do think the object on the left is? (The chair is only in the photo for a sense of scale.)
Posted in Uncategorized
Debugging code running 100 million miles away
From Lisping at JPL: Debugging a program running on a $100M piece of hardware that is 100 million miles away is an interesting experience. Having a read-eval-print loop running on the spacecraft proved invaluable in finding and fixing the problem.…
Numerical integration trick
Suppose you want to evaluate the following integral: We’d like to do a change of variables to make the range of integration finite, and we’d like the transformed integral to be easy to evaluate numerically. The change of variables t…
Math is like the Hawaiian islands
Keith Kendig compares math to the Hawaiian islands: Hawaii may look like a group of separate islands, but actually the islands are just the highest peaks of an immense, mostly-submerged mountain range. All that water hides their underlying connectedness, their…
SciPy integration misunderstanding
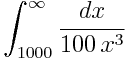
Today I needed to compute an integral similar to this: I used the following SciPy code to compute the integral: from scipy.integrate import quad def f(x): return 0.01*x**-3 integral, error = quad(f, 1000, sp.inf, epsrel = 1e-6) print integral, error…
Nicolas Bourbaki's wedding invitation
Nicolas Bourbaki was the collective pseudonym of a semi-secret group of French mathematicians, best known for the formal style of mathematics it promoted. The group insisted that Bourbaki was a real person, but only as a joke. The most recent…
Easiest and hardest classes to teach
I’ve taught a variety of math classes, and statistics has been the hardest to teach. The thing I find most challenging is coming up with homework problems. Most exercises are either blatantly artificial or extremely tedious. It’s hard to find…
Tagged with: Differential equations, Education, Probability and Statistics
Posted in Math, Statistics
Posted in Math, Statistics
Software to slice bread
In the dark ages of programming, functions acted on data. To slice your bread, you passed a bread data structure to a slice function: slice(bread); Then came object oriented programming. Instead of having an external function slice our bread, we…
Digital desk, analog desk
Austin Kleon has an interesting idea for setting up a workspace: have a digital desk and an analog desk. I have two desks in my office — one is “analog” and one is “digital.” The analog desk has nothing but…
Misplaced decimal
This evening I ran across a dialog that suggests that decimal notation is wrong. It happened when I started learning about decimals in school. I knew then that ten has one zero, a hundred has two, a thousand three, and…
iPad as hip flask
I reread Paul Graham’s essay The Acceleration of Addictiveness after a friend quoted it in a blog post explaining why he is taking an indefinite hiatus from social media. I hadn’t noticed this gem in the footnotes when I first…
