Month: October 2021

Unicode superscripts and subscripts

Posted on by John

There are alternatives to using <sup> and <sub> tags for superscripts and subscripts in HTML. These alternatives may look better, depending on context, and they can be used in plain (Unicode) text files where HTML markup isn’t available.

Superscripts

When I started blogging I would use <sup>2</sup> and <sup>3</sup> for squares and cubes. Then somewhere along the way someone told me about &sup2; (U+00B2) and &sup3; (U+00B3) and I started using these. The superscript characters generally produce slightly smaller subscripts and look nicer in my opinion.

Example with sup tags:

a2 + b2 = c2

Example with superscript characters:

a² + b² = c²

But there are no characters for exponents larger than 3. Or so I thought until recently.

There are no HTML entities for exponents larger than 3, nothing written in notation analogous to &sup2; and &sup3;. There are Unicode characters for other superscripts up to 9, but they don’t have corresponding HTML entities.

The Unicode code point for superscript n is

2070hex + n

except for n = 2 or 3. For example, U+2075 is a superscript 5. So you could write x⁵ as

<em>x</em>&#x2075;.

Subscripts

There are also Unicode symbols for subscripts, though they don’t have corresponding HTML entities. The Unicode code point for superscript n = 0, 1, 2, … 9 is

2080hex + n

For example, U+2087 is a subscript 7.

The subscript characters don’t extend below the baseline as far as subscripts in <sub> tags do. Here are x‘s with subsubcripts in <sub> tags.

x0, x1, x2, x3, x4, x5, x6, x7, x8, x9

And here are the single character subscripts.

x₀, x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉

I think the former looks better, but subscripts in HTML paragraphs may increase the vertical spacing between lines. If consistent line spacing is more important than conventional subscripts, you might prefer the subscript characters.

Related posts

Connections

Posted on by John

One of my favorite things in math is connecting together things that do not seem related at first. This post will elaborate on a connection between two recent posts.

Gauss’s constant

A couple weeks ago I wrote about Gauss’s constant

g \equiv \frac{1}{\text{AGM}(1, \sqrt{2})} = 0.834626\ldots

and several things it was related to. We can calculate g with n iterations of the process defining the AGM (arithmetic-geometric mean) as follows.

    def f(n):
        a, b = 1, 2**0.5
        for _ in range(n):
            a, b = 0.5*(a+b), (a*b)**0.5
        return 1/a

This process converges very quickly, calculating g to full machine precision when n = 4.

Elliptic integrals

Gauss’s constant, and the AGM more generally, can be computed in terms of an elliptic integral, and that in turn can be computed in terms of a hypergeometric function.

Elliptic integrals are so named because historically they are related to the problem of finding the perimeter of an ellipse. The particular elliptic integral we’re interested here is Legendre’s K function

K(k) = \int_0^{\pi/2} \frac{d\theta}{\sqrt{1 - k^2 \sin^2\theta}}

(There are several conventions for parameterizing elliptic integrals, so this definition may not match what you see elsewhere. See last section.)

With this definition of K,

\frac{1}{\text{AGM}(x,y)} = \frac{2}{\pi y} K(\sqrt{1 - y^2/x^2})

and by the symmetry of the AGM, you can reverse the order of x and y. It follows that

g = \frac{\sqrt{2}}{\pi}K\left(\frac{1}{\sqrt{2}}\right) = \frac{2}{\pi}K(i)

Hypergeometric functions

The previous post briefly introduced hypergeometric functions. The function K is related to Gauss’s hypergeometric function by

K(k) = \frac{\pi}{2} F\left(\frac{1}{2}, \frac{1}{2}; 1; k^2 \right)

Expanding F as a series shows the connection to double factorials.

\begin{align*} F\left(\frac{1}{2}, \frac{1}{2}; 1; x \right) &= \sum_{n=0}^\infty \frac{(1/2)_n (1/2)_n}{(1)_n n!} x^n \\ &= \sum_{n=0}^\infty \left( \frac{(2n-1)!!}{(2n)!!} \right)^2 x^n \end{align*}

This means you could numerically evaluate a power series to compute Gauss’s constant, thought that would be inefficient. Because the AGM converges so quickly, you’d want to evaluate elliptic integrals in terms of the AGM, not evaluate the AGM in terms of elliptic integrals.

Conventions

There is some confusing terminology and variation in conventions when defining elliptic integrals. We’ve defined K here in terms of the “elliptic modulus” k. Some software, such as Mathematica and SciPy, define K in terms of “the parameter” m = k². So to evaluate K above using Mathematica, you’d need to square the argument first.

    g = EllipticK[0.5] Sqrt[2]/Pi

or

    g = 2 EllipticK[-1]/Pi

Similarly, in Python we’d write

    from scipy.special import ellipk
    from math import pi
    g = ellipk(0.5)*2**0.5/pi

or

    g = 2*ellipk(-1)/pi

Foreshadowing hypergeometric functions

Posted on by John

I’ve said in several blog posts that multi-factorials come up often in practice, and given examples. This post will give a glimpse of why this is.

Rising powers

The kth rising power of a is

(a)k = a (a+1) (a + 2) … (a + k − 1).

So, for example, (5)3 = 5*6*7 and (1)k = n!.

Double factorials

Now let’s look at rising powers of fractions.

(1/2)k = (1/2) (3/2) (5/2) … (2k − 1)/2 = (2k −1)!! / 2k.

This means double factorials of odd numbers can be written as rising powers.

(2k −1)!! = 2k (1/2)k .

Now for even numbers,

(2k)!! = 2k k! = 2k (1)k

and so even double factorials can be written in terms of rising powers too. This means that the term

(2k − 1)!! / (2k)!!

from the series in the previous post could be written as

(1/2)k / (1)k .

Hmm. Ratios of rising powers sound useful.

Generalizing

From the discussion above you can imagine how to create triple factorials out of rising powers of 1/3 and 2/3. In fact it’s easy to see that all multifactorials can be made out of rising powers of rational numbers.

Ratios of multifactorials come up often in coefficients of power series, and these can be rewritten as ratios of rising powers. Maybe we should have a name for functions whose coefficients are ratios of rising powers. And we do: hypergeometric functions. You can find the exact definition here.

At first the definition of a hypergeometric function seems arbitrary. I hope my previous posts, and especially this post, has been a sort of warm up to motivate why you might be interested in such functions.

Applications

In an old post I quoted W. W. Sawyer saying

There must be many universities today where 95 percent, if not 100 percent, of the functions studied by physics, engineering, and even mathematics students, are covered by the single symbol F(a, b; c; x).

The notation F(a, b; c; x) here denotes the hypergeometric function whose kth power series coefficient is

(a)k (b)k / (c)k  k!

More general hypergeometric functions have two lists of parameters, separated by a semicolon. The first set corresponds to rising powers in the numerator, and the second set corresponds to rising powers in the denominator.

The exponential function is the simplest hypergeometric function: both parameter lists are empty, leaving only the k! term in the denominator.

The arcsine function mentioned above is an example of a function that is not hypergeometric per se, but can be written simply in terms of a hypergeometric function:

sin−1(x) = x F(1/2, 1/2; 3/2, x²).

This is more what Sawyer had in mind. Elementary functions like sine, cosine, and log note pure hypergeometric functions but are simply related to hypergeometric functions, similar to arcsine. The same is true of more advanced functions, like elliptic integrals and the CDFs of common probability distributions.

More on hypergeometric functions

Hidden double factorial example

Posted on by John

A while back I wrote several about multi-factorials and gave examples of triple factorials and quadruple factorials in action. I didn’t do a post on double factorials because they are more common. But an example I ran into recently changed my mind.

If you skim a table of power series you will run into a lot of examples of double factorials, or rather you will run into a lot of examples that could be written in terms of double factorials. However, some sources avoid this notation. This is unfortunate because the representation in terms of double factorials is often simpler or more symmetric than the alternatives. I’ll give one example here.

If you ask Wolfram Alpha for the power series for arcsine, you’ll get several representations, the simplest being

\sin^{-1}(x) = \sum_{k=0}^\infty \frac{\left(\frac{1}{2}\right)_k}{k! + 2 k k!}x^{1 + 2k}

Here the notation (a)k denotes Pochhammer symbol, the kth rising power of a. For details, see these notes.

The series is easier to understand written in terms of double factorials:

\sin^{-1}(x) = \sum_{k=0}^\infty \frac{(2k-1)!!}{(2k)!!}\frac{x^{2k+1}}{2k+1}

Here (−1)!! is defined to be 1. This may seem odd, but the series above is an example that shows the usefulness of this definition. Also, it can be shown that

z!! = 2^{(z-1)/2} \frac{\Gamma\left(\frac{z}{2} + 1 \right)}{\Gamma\left(\frac{1}{2} + 1 \right)}

and the expression on the right equals 1 when z = −1.

However, the series above also depends on the convention that 0!! = 1. This is a common convention, and it can be justified on the grounds that it is an empty product. However, the equation above relating double factorials to the gamma function yields √(2/π) at zero.

It would be interesting to look further into why there are two candidate definitions for 0!!. It seems like an example of the relatively rare occasions where algebraic and analytic conventions conflict. I suspect the 0!! = 1 convention is usually more convenient in applications, e.g. when working with power series, though it would depend on the application.

Euler polynomials

Posted on by John

The previous post looked at the logistic function and showed how it illustrates Runge’s phenomenon: adding interpolation points makes the interpolation error worse.

Here’s another interesting thing about the logistic function: it’s power series coefficients involve Euler polynomials.

\frac{e^x}{1 + e^x} = \sum_{n=0}^\infty \frac{x^n E_n(1)}{2 \, n!}

So, what are Euler polynomials? I don’t have a good answer to that, but I can say they’re closely related to several things I’ve written about lately.

There are multiple ways of defining the Euler polynomials, the most succinct being in terms of their generating function. That tells you what they are, in a sense, but it doesn’t answer the question of why Euler was interested in them, or why anyone else would be interested in them.

One thing I can say is they seem to pop up occasionally in combinatorics problems. They come up, for example, in the calculus of finite differences. Another is that they’re closely related to Bernoulli polynomials, and Bernoulli polynomials pop up even more often in combinatorics.

Three weeks ago I wrote about the sawtooth function and how it satisfies the multiplicative identity

f(nx) = \sum_{i=0}^{n-1} f\left(x + \frac{i}{n} \right )

Then a few days later I wrote about more general multiplication theorems. I mentioned the Bernoulli polynomials and how they satisfy the same identity, except for a factor that is independent of x.

B_m(nx) = a(m, n) \sum_{i=0}^{n-1} B_m\left(x + \frac{i}{n} \right)

The Euler polynomials satisfy an equation of the same form, but with an alternating term inside the sum.

E_m(nx) = a(m, n) \sum_{i=0}^{n-1} (-1)^i E_m\left(x + \frac{i}{n} \right)

For Bernoulli polynomials a(m, n) = nm−1.

For Euler polynomials a(m, n) = nm for odd n and −2/(m + 1) times that for even n.

Logistic counterexamples

Posted on by John

The function

f(x) = 1/(1 + x²)

is commonly used as an example to disprove a couple things students might be lead to believe. This post will show how the logistic function

g(x) = exp(x)/(1 + exp(x))

could be used in the same contexts. This shows that f(x) is not an isolated example, and the phenomena that it illustrates are not so rare.

Radius of convergence

One thing that f is commonly used to illustrate is that the power series of a function can have a finite radius even though the function is infinitely differentiable with no apparent singularities. I say “apparent” because the function f has no singularities as long as you think of it as a function of a real variable. When you think of it as a function of a complex variable, it has singularities at ±i.

The radius of convergence of a function is something of a mystery if you only look along the real line. (You may see “interval” of convergence in textbooks. I’m tipping my hand by using the word “radius.”) If a function has a power series in the neighborhood of a point, the radius of convergence for that series is determined by the distance to the nearest singularity in the complex plane, even if you’re only interested in evaluating the series at real numbers. For example,

f(x) = 1 − x2 + x4 − x6 + ⋯

The series converges for |x| < 1. If you stick in an x outside this range, say x = 3, you get the absurd [1] equation

1/10 = 1 − 9 + 81 − 729 + ⋯

The logistic function g also has a finite radius of convergence, even though the function is smooth everywhere along the real line. It has a singularity in the complex plane when exp(x) = −1, which happens at odd multiples of πi. So the power series for g centered at 0 has a radius of π, because that’s the distance from 0 to the nearest singularity of g.

Runge phenomenon

Carl David Tolmé Runge, best known for the Runge-Kutta algorithm, discovered that interpolating a function at more points may give worse results. In fact, the maximum interpolation error can go to infinity as the number of interpolation points increases. This is true for the Cauchy function f above, but also for the logistic function g. As before, the explanation lies in the complex plane.

Runge’s proved that trouble occurs when interpolating over the segment [−1, 1] at evenly-spaced points [2] if the function being interpolated has a singularity inside a certain region in the complex plane. See [3] for details.When we interpolate

g(x) = exp(ax)/(1 + exp(ax))

we can see the Runge phenomenon if a is large enough and if we interpolate at enough points. In the Mathematica code below, we use a = 10 and interpolate at 22 points.

    g[x_, a_] := Exp[a x]/(1 + Exp[a x])
    p[x_, a_, n_] :=  InterpolatingPolynomial[
        Table[{s, g[s, a]}, {s, -1.0, 1.0, 2/n}], x]
    Plot[{g[x, 10], p[x, 10, 22]}, {x, -1, 1}]

Here’s the plot.

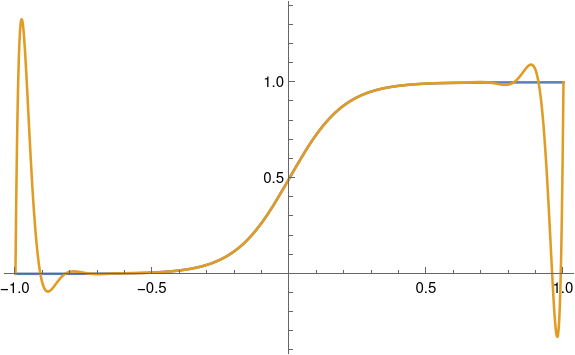
Note that we get a good fit over much of the interval; the two curves agree to within the thickness of a plotting line. But we get huge error near the ends. There we can see the flat blue line sticking out.

Obviously approximating a nearly flat function with a huge spike is undesirable. But even if the spikes were only small ripples, this could still be a problem. In some contexts, approximating a monotone function by a function that is not monotone can be unacceptable, even if the approximation error is small. More on that here.

Related posts

[1] You may have seen the “equation”

1 + 2 + 3 + ⋯ = −1/12.

This and the equation

1 − 9 + 81 − 729 + ⋯ = 1/10

are both abuses of notation with a common explanation. In both cases, you start with a power series for a function that is valid in some limited region. The left side of the equation evaluates that series where the series does not converge, and the right side of the equation evaluates an analytic continuation of the function at that same point. In the first example, the function is the Riemann zeta function ζ(s) which is defined by

\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}

for s with real part larger than 1. The series converges when the real part of s is larger than 1. The example evaluates the series at −1. The zeta function can be extended to a region containing −1, and there it has the value −1/12.


[2] You can avoid the problem by not using evenly spaced points, e.g. by using Chebyshev interpolation.


[3] Approximation Theory and Approximation Practice by Lloyd N. Trefethen

 

Dirichlet series generating functions

Posted on by John

A couple days ago I wrote about Dirichlet convolution, and in that post I said

Define the function ζ to be the constant function 1.

This was following the notation from the book I quoted in the post.

Someone might question the use of ζ because it is commonly used to denote the Riemann ζ function. And they’d be onto something: Calling the sequence of all 1’s ζ is sort of a pun on the ζ function.

Dirichlet series generating functions

Given a sequence a1, a2, a3, … its Dirichlet series generating function (dsgf) is defined to be

A(s) = \sum_{n=1}^\infty \frac{a_n}{n^s}

The Dirichlet series generating function for the sequence of all 1’s is the Riemann zeta function ζ(s).

\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}

The definition of ζ as a sequence was alluding to its associated Dirichlet series.

Dirichlet convolution

Recall from the earlier post that the Dirichlet convolution of two sequences is defined by

(f*g)(n) = \sum_{d|n} f(d) \,\,g\left(\frac{n}{d} \right)

A basic theorem connecting Dirichlet series and Dirichlet convolution says that if A(s) is the dsgf of

a1, a2, a3, …

and B(s) is the dsgf of

b1, b2, b3, …

then the dsgf of a*b, the Dirichlet convolution of the two series, is A(s) B(s).

In short, the dsgf of a convolution is the product of the dsgfs. This is an example of the general pattern that transforms turn convolutions into products. Different kinds of transformations have different kinds of convolution. See examples here.

Dirichlet series of an inverse

In the earlier post we defined the inverse of a sequence (with respect to Dirichlet convolution) to be the sequence you convolve it with to get the sequence δ(n) given by

1, 0, 0, 0, …

The dsgf of δ(n) is simply the constant 1. Therefore if a*b = δ, then AB = 1. Said another way, if a is the inverse sequence of b, then the dsgf of a is the reciprocal of the dsgf of b.

The earlier post defined the Möbius function μ(n) to be the inverse of the sequence of 1’s, and so its dsgf is the reciprocal of the zeta function.

\sum_{n=1}^\infty \frac{\mu(n)}{n^s} = \frac{1}{\zeta(s)}

Related posts

Unintended programming languages

Posted on by John

As I mentioned a few days ago, I’ve been looking at Remora, a sort of child of Lisp and APL. I find it interesting that neither Lisp nor APL were initially intended to be programming languages. (I also find it interesting that Lisp and APL are at opposite ends of the syntax spectrum, from minimal to maximal emphasis on notation.)

Lisp

John McCarthy developed Lisp as a theoretical construct. He didn’t intend it to actually run on a computer, and in fact he was surprised when Steve Russell turned Lisp into an actual programming language to run on the IBM 704.

McCarthy is usually given sole credit for developing Lisp, and if Russell is mentioned at all, he’s included as a footnote. You could argue this is backward and that Russell was the inventor of Lisp, with inspiration from McCarthy.

APL

APL is known for its idiosyncratic notation. What’s not as commonly known is that APL was originally intended to only be a system of notation. As explained here,

[APL] didn’t originate as a computer language at all. It was proposed as a better notation for tensor algebra by Harvard mathematician Kenneth E. Iverson. It was meant to be written by hand on a blackboard to transfer mathematical ideas from one person to another.

A few of Iverson’s notations have survived in common use in mathematics, but his larger impact has been through the application of his ideas for notation in array-oriented programming languages. While very few program in APL, a lot of people use ideas from APL which have been adopted by more popular languages, such as R and Python (in NumPy).

An interesting recursion

Posted on by John

The previous post concerned finding the inverse of a function with respect to Dirichlet convolution. Given a function f defined on the positive integers, we want to find a function g, also defined on positive integers, such that f*g = δ. This means we want to find a function g such that the sum

(f*g)(n) = \sum_{d|n} f(d) \,\,g\left(\frac{n}{d} \right)

evaluates to 1 if n = 1 and 0 otherwise.

We said in that post that the function g can be defined recursively by

g(1) =\frac{1}{f(1)}

and

g(n) = -\frac{1}{f(1)} \sum_{\stackrel{d > 1}{d|n}} f(d)\,\,g\left(\frac{n}{d} \right )

for n > 1.

Python code

We can implement this directly in Python as a recursive function. Starting with any function f, we can define g exactly as above. For simplicity we set f(n) = n in the code below.

    from sympy import divisors

    def f(n):
        return n

    def g(n):
        if n == 1:
            return 1/f(1)
        s = sum(f(d)*g(n//d) for d in divisors(n)[1:])
        return -s/f(1)

The function sympy.divisors returns a list of divisors of a number, sorted in increasing order. We use [1:] to exclude the 0th divisor, i.e. 1, to get the list of divisors greater than 1. The code terminates because d > 1, and so n/d < n.

Note that the code uses integer division in g(n//d). Since we’re dividing n by one of its divisors, n/d is (mathematically) an integer, but the Python code n/d would return a value of type float and cause Python to complain that an argument to g is not an integer.

What’s interesting about this recursion is the set of cases g is defined by. Often a recursive function of n is defined in terms of its value at n − 1, as in factorial, or its values at consecutive previous values, as in Fibonacci numbers. But here the value of g at n depends on the the values of g at factors of n.

So, for example, if we evaluate g(12), the code will evaluate g at 1, 2, 3, 4, and 6. In the process of computing g(12) we don’t need to know the value of g at 11.

Caching

Note that there’s some redundancy in the execution of our code. When we evaluate g at 4, for example, it evaluates g at 2, which had already been calculated. We could eliminate this redundancy by using memoization to cache computed values. In Python this can be done with the lru_cache decorator from functools.

    import functools

    @functools.lru_cache(maxsize=None)
    def g(n):
        if n == 1:
            return 1/f(1)
        s = sum(f(d)*g(n//d) for d in divisors(n)[1:])
        return -s/f(1)

If we use the revised code to calculate g(12), the call to g(6), for example, will look up the previously computed values of g(1), g(2), and g(3) from a cache.

If we evaluate g at several values, the code will fill in its cache in a scattered sort of way. If our first call is to evaluate g(12), then after that call the values of g at 1, 2, 3, 4, and 6 will be cached, but there will be no value of g at 7, for example, in the cache. If we then evaluate g(7), then this value will be cached, but there’s no value of g at 5 in the cache, and there won’t be until after we evaluate g at a multiple of 5.

Run time

Suppose the cache contains g(x) for all x < n and you want to compute g(n). How long would that take?

For large n, the number of divisors of n is on average about log(n), so the algorithm requires O(log n) look ups. For more detail, see the Dirichlet divisor problem. If you wanted to be more detailed in your accounting, you’d need to take into account the time required to produce the list of n‘s divisors, and the time required to look up cached values. But as a first approximation, the algorithm runs in O(log n) time.

I think the same is true even if you start with an empty cache. It would take longer in this case, but I think this would only change the size of the constant in front of log n.

Related posts

Dirichlet convolution

Posted on by John

That can’t be right

I was skimming a book on number theory [1] recently and came across the following theorem that makes no sense out of context:

An arithmetical function f has an inverse if and only if f(1) ≠ 0.

Wait, what?! That’s obviously false unless I’ve missed something. Maybe “arithmetical function” is far more restrictive than I thought.

No, in this book an arithmetical function is simply a function on positive integers. In general it can be complex-valued, though early in the book all the examples are integer or rational valued.

What I was missing was the meaning of “inverse.” My first thought was that it meant inverse with respect to composition, but it meant inverse with respect to convolution.

Dirichlet convolution

Given two arithmetic functions f and g, their Dirichlet convolution f*g is defined by

(f*g)(n) = \sum_{d|n} f(d) \,\,g\left(\frac{n}{d} \right)

The sum is over all divisors of n and so, for example, the value of f * g at 6 would be

f(1)g(6) + f(2)g(3) + f(3)g(2) + f(6)g(1)

It’s clear that convolution is commutative, and with a little more effort you can show that it’s associative.

There is an identity element for convolution, the function δ(n) defined to be 1 if n = 1 and 0 otherwise. For any arithmetical function f, clearly f*δ = f because all the terms in the sum defining (f*δ)(n) are zero except the term f(n).

Inverse

In the context of the theorem above, the inverse of a function f is another function g whose convolution with f gives the identity δ, i.e. g is the inverse of f if f*g = δ. Inverses, if they exist, are unique.

Now that we have the right definition of inverse in mind, the theorem above isn’t obviously false, but it’s not clear why it should be true. And it’s a remarkable statement: with just the slightest restriction, i.e. f(1) ≠ 0, every arithmetical function has an inverse with respect to convolution. Not only that, the proof is constructive, so it shows how to compute the inverse.

For an arithmetical function f with f(1) ≠ 0, define its inverse function g by

g(1) =\frac{1}{f(1)}

and for n > 1 define

g(n) = -\frac{1}{f(1)} \sum_{\stackrel{d > 1}{d|n}} f(d)\,\,g\left(\frac{n}{d} \right )

This definition is not circular even though g appears on both sides. On the right side g is only evaluated at arguments less than n since the sum restricts d to be greater than 1. The next post implements this recursive definition of g in Python.

Möbius inversion formula

Define the function ζ to be the constant function 1. Since ζ(1) is not zero, ζ has an inverse. Call that inverse μ.

If f = g*ζ, then convolution of both sides with μ shows that f*μ = g. This is the Möbius inversion formula.

When presented this way, the Möbius inversion formula looks trivial. That’s because all the hard work has been moved into prerequisites. Stated from scratch, the theorem is more impressive. Without using any of the definitions above, Möbius inversion formula says that if f is defined by

f(n) = \sum_{d|n}g(d)

then

g(n) = \sum_{d|n}f(d) \, \mu\left(\frac{n}{d} \right)

where

\mu(n) = \left\{ \begin{aligned} {1} &\mbox{\quad if } {n=1} \\ {0} &\mbox{\quad if } {a^2 \,|\, n \mbox{ for some } a > 1} \\ {(-1)^r} &\mbox{\quad if } {n \mbox{ has } r \mbox{ distinct prime factors}} \end{aligned} \right.

We initially defined μ implicitly as the inverse of the constant function 1. When written out explicitly we have the definition of the Möbius function μ above.

Related posts

[1] An Introduction of Arithmetical Functions by Paul J. McCarthy, Springer-Verlag, 1986.