Solving hard problems

We help companies solve hard problems in mathematics, statistics, and computing. Let’s explore how we might work together.

Why exponential sums are interesting

Posted on 26 May 2021 by John

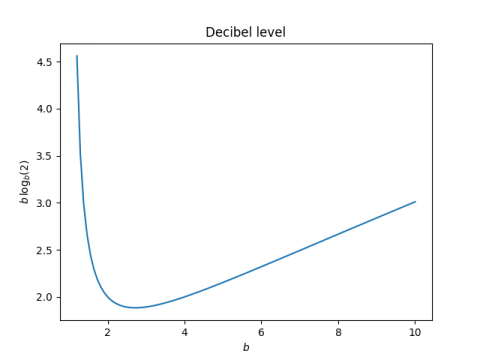
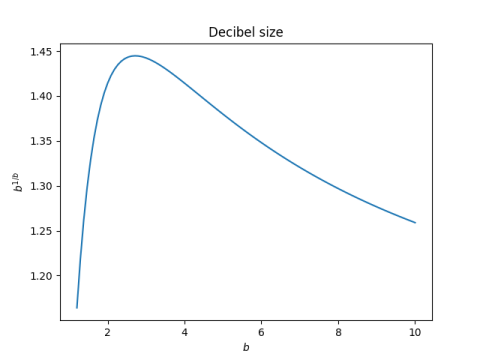
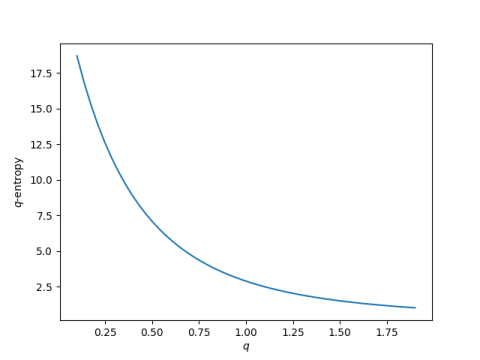
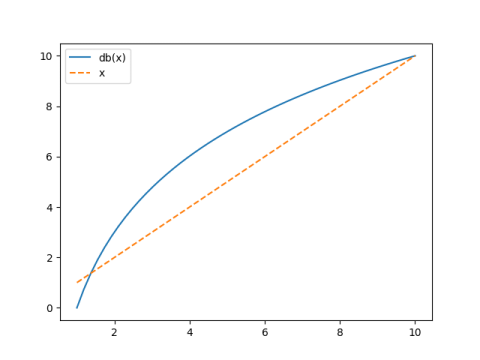
The exponential sum page on this site draws lines between the consecutive partial sums of

$\sum_{n=0}^N \exp\left( 2\pi i \left( \frac{n}{m} + \frac{n^2}{d} + \frac{n^3}{y} \right ) \right )$

where m is the month, d is the day, and y is the last two digits of the year.

I get mixed feedback on my exponential sum page. Some people find it even more interesting than I do and have asked permission to use the images [1]. Others tell me they don’t understand what the big deal is. I find the images interesting, and I’d like to give some explanation why.

What I like about these images is that they’re somewhere between predictable and mysterious. The particular sum above has a few properties that aren’t hard to derive, but it’s also full of surprises. This is true of exponential sums more generally.

Exponential sums can be deep and subtle. See, for example, the course description and lecture notes here. If you eliminate the linear and cubic components in the sum above, conceptually setting m and y to infinity, and d is a prime number, then you get the Gauss sums, a topic of particular interest in the lecture notes.

The contrast between images for consecutive days illustrates the fact that number theory has its own way of measuring differences (e.g. p-adic numbers). So, for example, while today’s date [2], 5/26/2021, is close to yesterday’s date, 5/25/2021, the corresponding images

Exponential sum for 2021-05-26, roughly circular

and

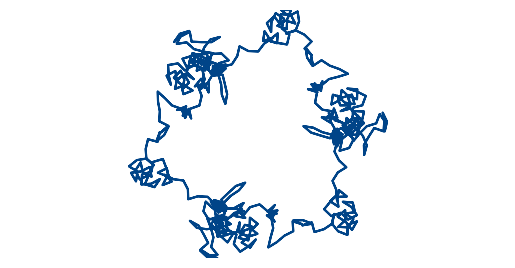
Exponential sum for 2021-05-25, very irregular

are very different because from a number theoretic perspective the triples (5, 26, 21) and (5, 25, 21) are not close together. The individual terms in the sums are close together, because 1/25 is close to 1/26, but the sums have quite different behavior.

Estimating exponential sums and proving things about them requires its own set of techniques. If you just apply the usual techniques you’d use on general sums, your estimates will be so far from optimal as to be useless.

I’m not an expert in exponential sums. When I look at the images my site produces I know that something is going on deeper than I understand, even though I can’t say what it is. That’s how most of the world is—there’s more to my car, or my dog, or even my fingernail than I’ll ever understand—but it’s even true of much simpler things, like exponential sums.

[1] If you’d like to use one of the images, go ahead. But rather than taking a screen shot, send me an email and I can give you a higher resolution image or an SVG file.

[2] I understand the objections to the American way of writing dates, but I thought the exponential sum page worked out to be more interesting basing it on this format. I prefer the ISO date format to both American and European conventions.

LaTeX and Lawyers

Posted on 24 May 2021 by John

Lawyers write Word documents and mathematicians write LaTeX documents. Of course makes collaboration awkward, but there are ways to make it better.

One solution is to simply use Word. People who use LaTeX probably know how to use Word, even if they’d rather not, and asking someone else to learn LaTeX is a non-starter. So if I’m coauthoring a document with a lawyer, I’ll use Word.

If I’m writing a report that a lawyer needs to review, I’ll use LaTeX. Using different programs actually helps because it makes a clear distinction between copy editing feedback and authorial responsibility.

This post will give a couple tips for writing reports in LaTeX to be delivered to a lawyer, one trivial and one not quite trivial.

The trivial tip is that \S produces the section sign § (U+00A7) common in legal documents but not so common elsewhere. The not so trivial tip is that the enumitem package lets you change the default labels that LaTeX uses with enumerated items.

Changing enumerated item labels

LaTeX was designed under the assumption that the user wants to focus on logical structure and leave the formatting up to the the typesetting program. Consistent with this design philosophy, nested enumerated lists simply wrapped with \begin{enumerate} and \end{enumerate} and individual list items are marked with \item, regardless of the level of nesting. LaTeX takes responsibility for displaying different labels at different levels: Arabic numerals for top-level lists, Roman letters for the next level of list, etc.

When you’re quoting legal documents, however, you don’t want to simply preserve the logical structure of (nested) lists; you want to preserve the labels as well.

Suppose you have the following nested list.

    \begin{enumerate} 
    \item First top-level item
    \item Second top-level item
      \begin{enumerate}
      \item A sub-item
      \item Another sub-item
        \begin{enumerate}
        \item A third-level item
        \item Another third-level item
          \begin{enumerate}
            \item Four levels in
            \end{enumerate}
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

By default, LaTeX will format this as follows.

But suppose in order to match another document you need the labels to progress as (a), (1), (A), and (i). The following LaTeX code will accomplish this.

    \begin{enumerate} [label={(\alph*)}]
    \item First top-level item
    \item Second top-level item
      \begin{enumerate} [label={(\arabic*)}]
      \item A sub-item
      \item Another sub-item
        \begin{enumerate} [label={(\Alph*)}]
        \item A third-level item
        \item Another third-level item
          \begin{enumerate} [label={(\roman*)}]
            \item Four levels in
            \end{enumerate}      
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

This produces the following.

Note the parentheses in the labels above. You can replace remove one or both, replace them with square brackets, add periods, etc. as the following example shows.

    \begin{enumerate} [label={\alph*)}]
    \item First top-level item
    \item Second top-level item
      \begin{enumerate} [label={\arabic*.}]
      \item A sub-item
      \item Another sub-item
        \begin{enumerate} [label={(\Alph*)}]
        \item A third-level item
        \item Another third-level item
          \begin{enumerate} [label={[\roman*]}]
            \item Four levels in
            \end{enumerate}      
        \end{enumerate}
      \end{enumerate}
    \end{enumerate}

Here’s what this looks like when compiled.

A Pattern Language

Posted on 22 May 2021 by John

A Pattern Language: Towns, Buildings, Construction

I first heard of the book A Pattern Language sometime in the 1990s. I had left academia, for the first time [1], and was working as a software developer. Although the book is about architecture, software developers were exited about the book because of its analogs to software development patterns. The “Gang of Four” book Design Patterns, a book about object oriented programming, was also popular at the time.

I now see more people citing A Pattern Language for its architectural content, though it’s still cited in software circles. A lot of people quote it on Twitter. I recently discovered @apatterntolearn, a Twitter account devoted to the book.

The book is commonly attributed to Christopher Alexander alone, but the dust jacket says “Christoper Alexander, Sara Ishikawa, Murray Silverstein with Max Jacobson, Ingrid Fiksdahl-King, Shlomo Angel.” It’s easier to just say Christopher Alexander. I imagine people who are fully aware of there being more authors use Alexander as a synecdoche.

Ever since I ran into the book over 20 years ago I’ve intended to read it someday. I finally bought a copy a few weeks ago. I’ve blitzed through it, and I intend to go back through it more slowly.

Many quotes that I’d seen from Alexander have resonated with me, and I expected the book to do the same. That wasn’t my experience at first.

The book starts out abstract and becomes more concrete. I think the most quoted parts are later in the book. A few of the early patterns are quirky and controversial [2], but the book soon moves on to patterns that are more concrete and more widely accepted. For example, about midway through the book is the following observation.

If two parts of an office are too far apart, people will not move between them as often as they need to; and if they are more than one floor apart, there will be almost no communication between the two.

I noticed this early on in my career and found it bewildering. But it’s absolutely true, and in fact I might change “more than one floor apart” to “even one floor apart.”

The book talks a great deal about how to foster community, something we desperately need. Architecture is not the cause of or cure for strife, but architecture can create an environment where human interaction likely to be more frequent and more pleasant.

[1] I either left academia once or twice, depending on whether MD Anderson Cancer Center counts as academia. MDACC is a strange mix of hospital and university. I’d say my job there was semi-academic. I did some research and teaching, but I also did some software development and project management.

[2] I can sympathize with some of the quirky and/or controversial statements.

Email subscription changing

Posted on 19 May 2021 by John

Email subscription for this site has been provided by Google Feedburner. This service is going away in July.

I don’t know yet what I will replace Feedburner with. Do any of you know of an alternative that automatically sends out email when there’s a new post?

I use Mail Chip to distribute by monthly newsletter, but I wouldn’t want to send out a “newsletter” manually with Mail Chimp every time I write a post.

RSS had a near-death experience when Google killed their popular RSS reader, but RSS still works. I much prefer RSS to email, but not everyone feels the same.

You can find more about RSS, email, and newsletter subscription to this blog here. You can also find my Twitter accounts here.

The base with the largest decibel

Posted on 18 May 2021 by John

This post is an expansion on a comment by Nathan Hannon:

My favorite definition of e is “the base whose version of the decibel is the largest”.

I hadn’t seen that before. Sounds interesting. What does it mean?

First attempt

My first thought was that the statement meant that the function

b log_b(x)

is largest when b = e.

It’s easier to do calculus with natural logs—that’s one reason advanced math almost exclusively uses natural logs—and so we’ll rewrite the expression above as

b log(x) / log(b)

where log without a subscript is natural log. If we differentiate this expression with respect to b, we get

(log(b) – 1) log(x) / (log(b))²

and this expression is zero, independent of x, when log(b) = 1, i.e. when b = e.

So to recap, for any fixed x, the expression

b log_b(x)

as a function of b has a critical point where b = e.

So that’s the maximum, right? No, it’s a minimum!

dB level of 2 as base changes

The value of x doesn’t change the shape of the curve and I arbitrarily chose x = 2 in the plot.

Second attempt

Looking back at the original statement, it says e is the base that maximizes the decibel, not the level measured in decibels. The unit in which levels are minimized is the one which maximizes the size of the unit. The original statement is right and my first reading of it was backward.

As I wrote about here, the function

b log_b(x)

is equivalent to the logarithm base b^1/b. This base is one “decibel,” using quotes because we’ve replaced the 10’s in the definition of decibel with an arbitrary base b. The base, the decibel unit, is maximized when b = e.

Size of a decibel as the base varies

Relating Rényi entropy and q-log entropy

Posted on 18 May 2021 by John

I’ve written before about Rényi entropy H_q and most recently q-log entropy S_q, two generalizations of Shannon entropy.

There are simple equations relating Rényi entropy and q-log entropy if we measure both in nats:

$\begin{align*} S_q &= \frac{1}{1-q} \left( \exp\left( (1-q) H_q\right) -1 \right) \\ H_q &= \frac{1}{1-q} \log\left( (1-q) S_q +1 \right) \\ \end{align*}$

I mentioned in the post on q-log entropy that there were two possible ways it could be defined. The equation above applies to what I called in that post S_q, not S ‘_q. In other words, it applies to the version that uses ln_q(1/p) and not the version that uses -ln_q(p). Recall that these are not equal unless q equals 1. When q does equal 1, then Rényi entropy and q-log entropy are the same as Shannon entropy.

Source: Tom Leinster, Entropy and Diversity: The Axiomatic Approach.

Generalizing Shannon entropy with q-logs

Posted on 17 May 2021 by John

The most common way to quantify entropy is Shannon entropy. That’s what people usually mean when they say “entropy” without further qualifications. A while back I wrote about Renyi entropy as a generalization of Shannon entropy. This time I’ll explore a different generalization called q-log entropy, a.k.a. Tsallis entropy.

The definition of Shannon entropy includes the logarithms of probabilities. If we replace these logarithms with a generalization of logarithms, we have a generalization of Shannon entropy.

q-logarithms

The generalization of logarithm we want to look at for this post is the q-logarithm. The natural logarithm is given by

$\ln(x) = \int_1^x t^{-1}\,dt$

and we can generalize this to the q-logarithm by defining

$\ln_q(x) = \int_1^x t^{-q}\,dt$

And so ln₁ = ln.

q-logarithm entropy

We can define q-log entropy (a.k.a. Tsallis entropy) by replacing natural log with q-log. However we run into a minor issue.

Shannon entropy (in nats, see [1]) can be defined as either

$S = \sum_{i=1}^n p_i \ln\left(\frac{1}{p_i}\right)$

$S' = - \sum_{i=1}^n p_i \ln p_i$

These are equivalent because

$\ln\left(\frac{1}{x}\right) = -\ln(x)$

However

$\ln_q\left(\frac{1}{x}\right) \ne -\ln_q(x)$

unless q = 1.

On the other hand, it’s easy to show that

$\ln_q\left(\frac{1}{x}\right) = -\ln_{2-q}(x)$

And so we could use either ln_q(1/p) or -ln_q(p) in our definition of q-log entropy.

$\begin{align*} S_q &= \sum_{i=1}^n p_i \ln_q\left(\frac{1}{p_i}\right) \\ S'_q &= -\sum_{i=1}^n p_i \ln_q(p_i) \end{align*}$

The two definitions are not equivalent unless q = 1, but they are related by

$\begin{align*} S_q &= \sum_{i=1}^n p_i \ln_q\left(\frac{1}{p_i}\right) \\ S'_q &= -\sum_{i=1}^n p_i \ln_q(p_i) \end{align*}$

Example

To see q-log entropy in action, we’ll plot the entropy of the English alphabet as q varies.

English alphabet q-log entropy as q varies

This plot was made using English letter frequencies from here and the following Python code.

    def lnq(x, q):
        if q == 1:
            return np.log(x)
        t = 1 - q
        return (x**t - 1) / t

    def shannon_entropy(ps, base=2):
        s = sum(p*np.log(1/p) for p in ps)
        return s/np.log(base)

    def qlog_entropy(ps, q):
        return sum(p*lnq(1/p, q) for p in ps)

The Shannon entropy of the English alphabet is 2.8866 nats [2]. The q-log entropy is greater than that for q less than 1, and smaller than that for q greater than 1.

[1] Shannon entropy is usually defined in terms of logarithms base 2, i.e. entropy is usually measured in bits. If we change the base of the logarithm, we only multiply the result by a constant. So we can define Shannon entropy using natural logarithms, resulting in entropy measured in “nats.” More on bits, dits, and nats here.

[2] Or 4.1645 bits. See [1] above for the difference between bits and nats.

Stumbling on an abandoned uranium mine

Posted on 17 May 2021 by John

Last week my family and I made a tour of the five national parks in Utah. In Canyonlands National Park, my son-in-law noticed some grates at the bottom of a hill just a few feet off the road we were walking on. The area was not restricted.

We walked over to investigate and found that these grates blocked entrances to an abandoned uranium mine.

Uranium mine grates

The following photo was taken from the outside, looking through one of the grates. We weren’t foolish enough to try to get inside.

Uranium mine

Radiation is the least of the dangers. The top sign warns you not to spend more than a day in the area, but even that may be overly cautious. Unprocessed uranium is far less radioactive than most people think, and signs say that miners never found that much uranium in the park.

The bottom sign warns that if you get past the grates, you could suffocate from lack of oxygen, die from poisonous gas, fall through unstable rock, or even disturb a bat habitat.

Here’s a transcript of the first paragraph of the bottom sign.

This gate was installed for your safety and for the protection of an important bat habitat. Your cooperation is greatly appreciated in helping to preserve this environment by not attempting to bypass or vandalize this gate. If you manage to get inside, you could place yourself in great danger from oxygen-deficient air, toxic gases, unstable rock, and vertical drop-offs, and you might harm the bats within by disturbing their habitat.

Decibel to log in new base

Posted on 16 May 2021 by John

Logarithms in all bases are proportional. Specifically

log_a(x) = log_b(x) / log_b(a)

for any bases a and b. One way to read this is to say that if you already know about logarithms base b, logarithms base a aren’t anything fundamentally new [1]. They’re proportional to logarithms base b, and in fact the proportionality constant is 1/log_b(a).

This post would like to turn the discussion above around: a multiple of a logarithm is just a logarithm in another base, and it’s easy to find what that new base is.

The most famous function that is a multiple of a logarithm might be the function that converts numbers to decibel scale:

f(x) = 10 log₁₀(x).

This is a multiple of a logarithm, and so there is some base b such that f(x) is log base b.

It turns out b is 10^1/10. That is, decibel levels are logarithms base

b = 10^1/10 = 1.2589

So multiplying something by 1.2589 increases its decibel level by 1. That is, making something 1/4 larger increases its decibel level by slightly less than 1. [2]

Where did this b come from? How can we show that it’s correct?

Let’s start by finding the inverse of f. The function f does two things to x: it takes the log base 10, then multiplies by 10. Its inverse undoes things in the opposite order, i.e. it divides by 10 and raises 10 to the result.

f ^-1(x) = 10^x/10.

Now

10^x/10 = (10^1/10)^x

and so the inverse of f is the function that takes 10^1/10 to the power x. That means f must be the logarithm of x in base 10^1/10.

For possible future reference, let’s solve this problem in a little more generality, converting any multiple of a logarithm in any base to logarithm in another base.

f(x) = c log_a(x) = log_b(x)

then

f ^-1(x) = a^x/c = (a¹^/c)^x = b^x

and so

b = a¹^/c.

[1] It is convenient to use logarithms in different bases in different contexts even though they’re all proportional, just as it’s convenient to measure angles sometimes in degrees and sometimes in radians, even thought degrees and radians are proportional.

[2] So why think of decibels as 10 log₁₀ rather that log base 10^1/10? Because the former is much easier to conceptualize. Natural logarithms are easier to work with theoretically, but logarithms base 10 are easier to work with mentally.

And why multiply the decimal log by 10? Because then for single digit numbers, the original value and its decibel value have the same order of magnitude. And when x = 10, the two are equal.

graph of x and 10 log_10(x)

Most popular posts this year

Posted on 12 May 2021 by John

Here are the five most popular posts so far this year.

The posts above had the most page views. But just counting page views doesn’t measure what regular readers necessarily most enjoy reading. It’s heavily influenced by what gets shared on Hacker News and elsewhere, and so naturally favors the most accessible posts.

It’s harder to say which posts have gotten the most feedback because this isn’t as quantifiable and I’m drawing on memory. But I do remember getting a lot of feedback regarding my post More Stability, Less Stress about my experience consulting. I also got a lot of feedback regarding making interesting images using a strange coordinate system.

Solving hard problems

Why exponential sums are interesting

Related posts

LaTeX and Lawyers

Changing enumerated item labels

Related posts

A Pattern Language

Email subscription changing

Related links

The base with the largest decibel

First attempt

Second attempt

Relating Rényi entropy and q-log entropy

Generalizing Shannon entropy with q-logs

q-logarithms

q-logarithm entropy

Example

Related posts

Stumbling on an abandoned uranium mine

Decibel to log in new base

Related posts

Most popular posts this year