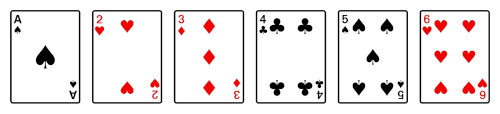
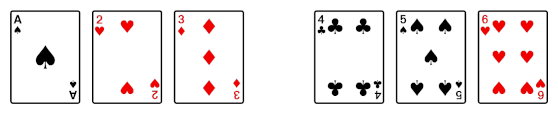
The previous post talked about doing perfect shuffles: divide a deck in half, and alternately let one card from each half fall.

It matters which half lets a card fall first. If the top half’s bottom card falls first, this is called an in-shuffle. If the bottom half’s bottom card falls first, it’s called an out-shuffle.

With an out-shuffle, the top and bottom cards don’t move. Presumably it’s called an out-shuffle because the outside cards remain in place.

An out-shuffle amounts to an in-shuffle of the inner cards, i.e. the rest of the deck not including the top and bottom card.

The previous post had a Python function for doing an in-shuffle. Here we generalize the function to do either an in-shuffle or an out-shuffle. We also get rid of the list comprehension, making the code longer but easier to understand.

def shuffle2(deck, inside = True):
    n = len(deck)
    top = deck[: n//2]
    bottom = deck[n//2 :]
    if inside:
        first, second = bottom, top
    else:
        first, second = top, bottom
    newdeck = []
    for p in zip(first, second):
        newdeck.extend(p)
    return newdeck

Let’s use this code to demonstrate that an out-shuffle amounts to an in-shuffle of the inner cards.

deck = list(range(10))
d1 = shuffle2(deck, False) 
d2 = [deck[0]] + shuffle2(deck[1:9], True) + [deck[9]]
print(d1)
print(d2)

Both print statements produce [0, 5, 1, 6, 2, 7, 3, 8, 4, 9].

I said in the previous post that k perfect in-shuffles will restore the order of a deck of n cards if

2^k = 1 (mod n + 1).

It follows that k perfect out-shuffles will restore the order of a deck of n cards if

2^k = 1 (mod n − 1)

since an out-shuffle of n cards is essentially an in-shuffle of the n − 2 cards in the middle.

So, for example, it only takes 8 out-shuffles to return a deck of 52 cards to its original order. In the previous post we said it takes 52 in-shuffles, so it takes a lot fewer out-shuffles than in-shuffles.

It’s plausible to conjecture that it takes fewer out-shuffles than in-shuffles to return a deck to its initial order, since the former leaves the two outside cards in place. But that’s not always true. It’s true for a deck of 52 cards, but not for a deck of 14, for example. For a deck of 14 cards, it takes 4 in-shuffles or 12 out-shuffles to restore the deck.

There are several numbers that are analogous to binomial coefficients and, at least in Donald Knuth’s notation, are written in a style analogous to binomial coefficients. And just as binomial coefficients can be arranged into Pascal’s triangle, these numbers can be arranged into similar triangles.

In Pascal’s triangle, each entry is the sum of the two above it. Specifically,

The q-binomial coefficients satisfy two similar identities.

Here are the analogous theorems for Stirling numbers of the first

and second

kinds.

And finally, here is the corresponding theorem for Eulerian numbers.

One day Eric Temple Bell (1883–1960) was looking at the power series for the double exponential function, exp(exp(x)) and noticed a similarity to the power series for exp(x). You can find his account in [1]. He would have calculated the series by hand, but we have the advantage of software like Mathematica.

We can get the first five terms of the series, centered at 0, with the command

    Series[Exp[Exp[x]], {x, 0, 5}]

This give us

If you pull out the factor of e from each term, and change the denominators to match those in the power series for exp(x) you get

with integers in all the numerators. It’s not obvious a priori that these numbers should even be integers, but they are,

Bell called the sequence numerators the exponential numbers: 1, 1, 2, 5, 15, 52, … The sequence is now known as the Bell numbers despite Bell’s modesty. Bell wasn’t the first to study this sequence of numbers, but he developed their properties more fully.

Applications

Bell numbers come up a lot in applications, which is why Bell wasn’t the first to notice them. (He may have been the first to come to them via their exponential generating function.) For example, the nth Bell number B_n is the number of ways to partition a set of n labeled items. B_n is also the nth moment of a Poisson random variable with λ = 1.

Bell’s triangle

There is a construction of Bell numbers analogous to Pascal’s triangle. Charles Sanders Peirce discovered what we now call Bell’s triangle fifty years before Bell discovered the Bell numbers.

To create Bell’s triangle, start with a row containing only 1.

The first number in each successive row is set to the last number in the previous row.

Then fill in the rest of the row by adding the number to the left and the number directly above

    1
    1  2
    2  3  5
    5  7 10 15
   15 20 27 37 52
   …

The numbers in the first column are the Bell numbers.

Related posts

• Bell numbers
• Number of groups of a given order
• Pascal’s triangle and the negative binomial distribution
• Special numbers

[1] E. T. Bell. Exponential Numbers. The American Mathematical Monthly, Vol. 41, No. 7 (Aug. – Sep., 1934), pp. 411–419.

The previous post looked at how to compute Q(n), the number of permutations of 1, 2, 3, …, n + 1 that contain no consecutive integers. We found a way to numerically compute Q(n) but no analytic expression that would let us compute asymptotics.

The sequence Q(n) is sequence A000255 in OEIS, and OEIS gives the exponential generating function of Q:

We can use this function and Theorem 5.2.1 from [1] to get the asymptotic form of Q(n). According to that theorem, the coefficient of xⁿ in our generating function is asymptotically the same as the coefficient of xⁿ in the principle part at the singularity at 1. This principle part is

and so the coefficient of xⁿ is (n + 2)/e.

So

and Q(n) / (n + 1)! approaches 1/e for large n, as conjectured in the previous post.

[1] Herbert S. Wilf. Generatingfunctionology. Second edition.

I was working on something this week that made me wonder how many permutations break up all consecutive elements. For example, if we’re looking at permutations of abcde then acebd counts, but acdbe does not. I’d like to count the number of such permutations, and estimate for large N the number of permutations of N elements with no consecutive terms.

A brief search lead to OEIS sequence A000255 which gives a recursive formula for the answer. Before looking at that, let’s define some terms and do some brute force calculation to get a feel for the problem.

Brute force calculation

Given a positive integer n, define Q(n) to be the number of partitions p of 1, 2, 3, …, n + 1 such that for no k does p(k + 1) = p(k) + 1.

from itertools import permutations

def no_consec(perm):
    for k in range(len(perm) - 1):
        if perm[k+1] == perm[k] + 1:
            return False
    return True

def Q(n):
    count = 0
    for p in permutations(range(n+1)):
        if no_consec(p):
            count += 1
    return count

We could use this code to compute Q(n) for moderate-sized n, but the time required to compute Q(n) this way is proportional to n! and so that won’t scale well.

Recurrence relation

OEIS sequence A000255 gives the values of what we’re calling Q(n), and the first few values match the output of the code above. But OEIS does better, giving a recursive solution for Q:

Q(n) = n Q(n − 1) + (n − 1) Q(n − 2)

for n > 1 with initial conditions Q(0) = Q(1) = 1.

As with Fibonacci numbers, you could implement this easily as a recursive function

def Q2(n):
    if n in[0, 1]:
        return 1
    return n*Q2(n-1) + (n-1)*Q2(n-2)

but it is much faster to implement iteratively.

def Q3(n):
    q = [1]*(n+2)
    for k in range(2, n+1):
        q[k] = k*q[k-1] + (k-1)*q[k-2]
    return q[n]

You could make the recursive implementation faster with memoization, using lru_cache from functools. However, memoization does not prevent recursion; it just speeds up recursion using a cache, and you can still get an error saying maximum recursion depth exceeded.

Asymptotics

We can calculate Q(n) for large n, but we don’t have an analytic expression [1] that will let us find the asymptotic behavior. I intended to work that out in my next post.

Empirically, it seems Q(n) approaches (n + 1)!/e as n goes to infinity, but I don’t have a proof of that at the time of writing. If this is correct, this means that in the limit the probability of a permutation having no fixed point equals the probability of it having no consecutive values.

Update: Proof

***

[1] There is an analytic expression for Q(n) in terms of a hypergeometric function

Q(n) = (−1)ⁿ ₂F₀(2, −n; ; 1)

but this expression isn’t helpful in finding the asymptotic behavior.