This post will look at how to take an expression for a Boolean function and look for a simpler expression that corresponds to the same function. We’ll show how to use a Python implementation of the Quine-McCluskey algorithm.
Notation
We will write AND like multiplication, OR like addition, and use primes for negation. For example,
wx + z‘
denotes
(w AND x) OR (NOT z).
Minimizing expressions
You may notice that the expression
wx‘z + wxz
can be simplified to wz, for example, but it’s not feasible to simplify complicated expressions without a systematic approach.
One such approach is the Quine-McCluskey algorithm. Its run time increases exponentially with the problem size, but for a small number of terms it’s quick enough [1]. We’ll show how to use the Python module qm which implements the algorithm.
Specifying functions
How are you going to pass a Boolean expression to a Python function? You could pass it an expression as a string and expect the function to parse the string, but then you’d have to specify the grammar of the little language you’ve created. Or you could pass in an actual Python function, which is more work than necessary, especially if you’re going to be passing in a lot of expressions.
A simpler way is pass in the set of places where the function evaluates to 1, encoded as numbers.
For example, suppose your function is
wxy‘z + w‘xyz‘
This function evaluates to 1 when either the first term evaluates to 1 or the second term evaluates to 1. That is, when either
(w, x, y, z) = (1, 1, 0, 1)
or
(w, x, y, z) = (0, 1, 1, 0).
Interpreting the left sides as binary numbers, you could specify the expression with the set {13, 6} which describes where the function is 1.
If you prefer, you could express your numbers in binary to make the correspondence to terms more explicit, i.e. {0b1101,0b110}.
Using qm
One more thing before we use qm: your Boolean expression might not be fully specified. Maybe you want it to be 1 on some values, 0 on others, and you don’t care what it equals on the rest.
The qm module lets you specify these with arguments ones, zeroes, and dc. If you specify two out of these three sets, qm will infer the third one.
For example, in the code below
from qm import qm
print(qm(ones={0b111, 0b110, 0b1101}, dc={}))
we’re asking qm to minimize the expression
xyz + xyz‘ + wxy‘z.
Since the don’t-care set is empty, we’re saying our function equals 0 everywhere we haven’t said that it equals 1. The function prints
['1101', '011X']
which corresponds to
wxy‘z + w‘xy,
the X meaning that the fourth variable, z, is not part of the second term.
Note that the minimized expression is not unique: we could tell by inspection that
xyz + xyz‘ + wxy‘z.
could be reduced to
xy + wxy‘z.
Also, our code defines a minimum expression to be one with the fewest sums. Both simplifications in this example have two sums. But xy + wxy‘z is simpler than wxy‘z + w‘xy in the sense of having one less term, so there’s room for improvement, or at least discussion, as to how to quantify the complexity of an expression.
In the next post I use qm to explore how much minimization reduces the size of Boolean expressions.
***
[1] The Boolean expression minimization problem is in NP, and so no known algorithm that always produces an exact answer will scale well. But there are heuristic algorithms like Espresso and its variations that usually provide optimal or near-optimal results.
![\begin{table}[] \begin{tabular}{lccll} & \phantom{i}add\phantom{i} & mult & & \\ \cline{2-3} \multicolumn{1}{l|}{conjunction} & \multicolumn{1}{c|}{\&} & \multicolumn{1}{c|}{\otimes} & & \\ \cline{2-3} \multicolumn{1}{r|}{disjunction} & \multicolumn{1}{c|}{\oplus} & \multicolumn{1}{c|}{\parr} & & \\ \cline{2-3} & & & & \end{tabular} \end{table}](https://www.johndcook.com/linear_con_dis_add_mult.png)
![\begin{table}[] \begin{tabular}{lcccl} & add & mult & exp & \\ \cline{2-4} \multicolumn{1}{r|}{positive} & \multicolumn{1}{c|}{\oplus} & \multicolumn{1}{c|}{\otimes} & \multicolumn{1}{c|}{!} & \\ \cline{2-4} \multicolumn{1}{r|}{negative} & \multicolumn{1}{c|}{\&} & \multicolumn{1}{c|}{\parr} & \multicolumn{1}{c|}{?} & \\ \cline{2-4} \end{tabular} \end{table}](https://www.johndcook.com/linear_pos_neg_add_mult_exp.png)
![]()
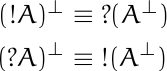
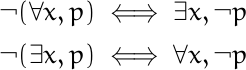


![data = [0, 0, 0, 0, 4, 44, 145, 339, 296, 128, 38, 5, 0, 1]](https://www.johndcook.com/bool_hist.png)