Math

Galois connections and Galois theory

Posted on by John

What are Galois connections and what do they have to do with Galois theory?

Galois connections are much more general than Galois theory, though Galois theory provided the first and most famous example of what we now call a Galois connection.

Galois connections

Galois connections are much more approachable than Galois theory. A Galois connection is just a pair of functions between partially ordered sets that have some nice properties. Specifically, let (A, ≤) and (B, ≤) be partially ordered sets. Here “≤” denotes the partial order on each set, and so could be defined differently on A and B.

We could add subscripts to distinguish the two meanings of ≤ but this is unnecessary because the meaning is always clear from context: if we’re comparing two things from A, we’re using the ≤ operator on A, and similarly for B.

Note that “≤” could have something to do with “less than” but it need not; it represents a partial order that may or may not be helpful to think of as “less than” or something analogous to less than such as “contained in.”

Monotone and antitone functions

Before we can define a Galois connection, we need to define monotone and antitone functions.

A monotone function is an order preserving function. That is, a function f is monotone if

x ≤ y ⇔ f(x) ≤ f(y).

Similarly, an antitone function is order reversing. That is, a function f is antitone if

x ≤ y ⇔ f(x) ≥ f(y).

Here ≥ is defined by

y ≥ x ⇔ x ≤ y.

Monotone and antitone connections

Galois connections have been defined two different ways, and you may run into each in different contexts. Fortunately it’s trivial to convert between the two definitions.

The first definition says that a Galois connection between A and B is a pair of monotone functions F and G such that for all a in A and b in B,

F(a) ≤ b⇔ a ≤ G(b).

The second definition says that a Galois connection between A and B is a pair of antitone functions F and G such that for all a in A and b in B,

F(a) ≤ b⇔ a ≥ G(b).

If you need to specify which definition you’re working with, you can call the former a monotone Galois connection and the latter an antitone Galois connection. We only need one of these definitions: if we reverse the definition of ≤ on B then a monotone connection becomes antitone and vice versa. [1]

How can we just reverse the meaning of ≤ willy-nilly? Recall that we said above that ≤ is just a notation for a partial order. There’s no need for it to mean “less than” in any sense, and the opposite of a partial order is another partial order.

We’ll use the antitone definition for the rest of the post because our examples are antitone. Importantly, the Fundamental Theorem of Galois Theory involves an antitone connection.

Examples

For our first example, let A be sets of points in the plane, and let B be sets of lines in the plane. For both sets let ≤ mean subset.

For a set of points X, define F(X) to be the set of lines that go through all the points of X.

Similarly, for a set of lines Y, define G(Y) to be the set of points on all the lines in Y.

Then the pair (F, G) form a Galois connection.

This example can be greatly generalized. Let R be any binary relation between A and B and let ≤ mean subset.

Define

F(X) = { y | x R y for all x in X }

G(Y) = { x | x R y for all y in Y }

Then the pair (F, G) form a Galois connection. The example above is a special case of this construction where x R y is true if and only if x is a point on y. Garrett Birkhoff made this observation in 1940 [2].

Galois theory

Galois theory is concerned with fields, extension fields, and automorphisms of fields that keep a subfield fixed.

I recently wrote a series of blog posts explaining what images on the covers of math books were about, and one of these posts was an explanation of the following diagram:

 

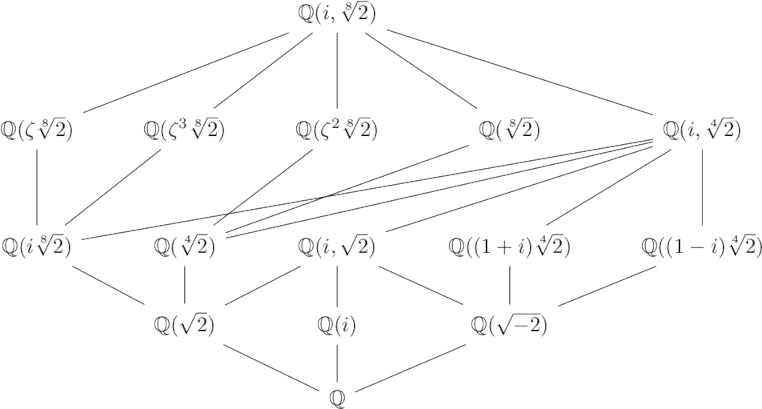
Each node in the graph is a field, and a line means the field on the higher level is an extension of the field on the lower level. For each graph like this of extension fields, there is a corresponding graph of Galois groups. Specifically, let L be the field at the top of the diagram and let E be any field in the graph.

The corresponding graph of groups replaces E with the group of group isomorphisms from L to L that leave the elements of E unchanged, the automorphisms of L that fix E. This map from fields to groups is half of a Galois connection pair. The other half is the map that takes each group to the field of elements of L fixed by G. This connection is antitone because if a field F is an extension of E, then the group of automorphisms that fix F are a subgroup of the automorphisms that fix E.

***

[1] We could think of A and B as categories, where there is a morphism between x and y iff x ≤ y. Then a monotone Galois connection between A and B is an antitone Galois connection between A and Bop.

[2] Garrett Birkhoff. Lattice Theory. American Mathematical Society Colloquium Publications, volume 25. New York, 1940.

Galois diagram

Posted on by John

The previous post listed three posts I’d written before about images on the covers of math books. This post is about the image on the first edition of Dummit and Foote’s Abstract Algebra.

Here’s a version of the image on the cover I recreated using LaTeX.

The image on the cover appears on page 495 and represents extension fields. If you’re going through this book sequentially as a text book, it’s likely time will run out before you ever find out what the image on the cover means. If you do get to it, you get to it near the end of your course.

My diagram is topologically equivalent to the original. I took the liberty of moving things around a bit to keep the diagram from being awkwardly wide.

At the bottom of the diagram we have ℚ, the field of rational numbers. At the top of the diagram we have ℚ(i, 21/8), the smallest field containing the rational numbers, the imaginary unit i, and the eighth root of 2. Lines between fields on two levels indicate that the higher is an extension of the lower. The constant ζ in the diagram is

ζ = √i = √2(1 + i)/2.

The significance of the diagram is that extension field relationships like these are important in Galois theory. The image appears late in the book because the majority of the book is leading up to Galois theory.

Book cover posts

Posted on by John

When a math book has an intriguing image on the cover, it’s fun to get to the point in the book where the meaning of the image is explained. I have some ideas for book covers I’d like to write about, but here I’d like to point out three such posts I’ve already written.

Weierstrass elliptic function

The book on the left is Abramowitz and Stegun, affectionately known as A&S. I believe the function plotted on the cover is the Weierstrass elliptic function, as I wrote about here.

As the image suggests, my copy of A&S has seen a bit of wear. At one point the cover fell off and I put it back on with packing tape.

Möbius transformation of circles

The book in the middle is my well-worn copy of my undergraduate complex analysis text. The cover is a bit dirty and pages are falling out, a sort of Velveteen rabbit of math books.

I haven’t written a post about the cover per se, but I did write about the necessary math to recreate the image on the cover here. That post explains how to compute the image of a circle under a Möbius transformation. The image on the left is mapped to the image on the right via the function

f(z) = 1/(z – α).

Here α is the point on the right where all the outer circles are tangent. If you wanted to reconstruct the image on the cover, it would be easier to proceed from right to left: start with the image on the right because it’s easier to describe, and apply the inverse transformation using the instructions in the blog post to produce the image on the left.

Hankel functions

I wrote about the book on the right here. I believe the image on the cover is the plot of a Hankel function.

Updates

Here’s a post explaining the image on the cover Abstract Algebra by Dummit and Foote.

And here is a post explaining the image on the cover of A Course of Modern Analysis by Whittaker and Watson.

 

Ducci sequences

Posted on by John

Pick four integers a, b, c, and d. Now iterate the procedure that takes these four integers to

|b – a|, |c – b|, |d – c|, |a – d|

You could think of the four integers being arranged clockwise in a circle, taking the absolute value of difference between each number and its neighbor a quarter turn clockwise. The sequence of 4-tuples created this way is called a Ducci sequence.

We can play with Ducci sequences using the following Python code.

    def next(x):
        n = len(x)
        return [abs(x[i] - x[(i+1)%n]) for i in range(n)]

If we start with four numbers taken from today’s date, the sequence will terminate in zeros in five steps. The code

    x = [7, 10, 20, 22]
    for _ in range(5):
        x = next(x)
        print(x)

This produces

    [3, 10, 2, 15]
    [7, 8, 13, 12]
    [1, 5, 1, 5]
    [4, 4, 4, 4]
    [0, 0, 0, 0]

The sequence always terminates for any starting point, and usually it terminates quickly, as in the example below. However, you can find starting values so that the sequence takes arbitrarily long to terminate.

In fact, the worse case for termination comes from consecutive Tribonacci numbers [1]. These numbers are defined analogously to Fibonacci numbers, but starting with 0, 0, 1, and each subsequent number being the sum of the previous 3 numbers.

0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, …

If you start with Tn, Tn+1, Tn+2, Tn+3 then the corresponding Ducci sequence takes at least 3n/2 steps to converge to 0.

Note that the code above does not assume we use sequences of 4 numbers. If we use n-tuples where n is a power of 2, the Ducci sequence always terminates in zeros. More generally the sequence will terminate in a cycle.

For example, suppose we start with 7, 10, and 22. Then the sequence of iterations is

    [3, 12, 15]
    [9, 3, 12]
    [6, 9, 3]
    [3, 6, 3]
    [3, 3, 0]
    [0, 3, 3]
    [3, 0, 3]
    [3, 3, 0] 
    ...

***

[1] Achim Clausing, Ducci Matrices. American Mathematical Monthly, December 2018.

Dijkstra extends Pythagoras

Posted on by John

Suppose a triangle has sides a, b, and c. Label the angles opposite these three sides α, β, and γ respectively.

Edsger Dijkstra published (EWD975) a note proving the following extension of the Pythagorean theorem:

sgn(α + β – γ) = sgn(a² + b² – c²).

Here the sgn function is -1, 0, or 1 depending on whether its input is negative, zero, or positive.

To see that this really is an extension of the Pythagorean theorem, if γ is a right angle, then α + β = γ and so the sgn on the left hand side evaluates to 0. This forces the right hand side to 0, which says a² + b² = c².

As Dijkstra points out, his is a theorem about triangles, not simply a theorem about right triangles.

More Dijkstra posts

Bump functions

Posted on by John

A bump function is a smooth (i.e. infinitely differentiable) function that is positive on some open interval (a, b) and zero outside that interval. I mentioned bump functions a few weeks ago and discussed how they could be used to prevent clicks in radio transmissions.

Today I ran into a twitter thread that gave a more general construction of bump functions that I’d seen before. The thread concludes with this:

You can create bump functions by this recipe:

    1. Take any f(x) growing faster than polynomial (e.g. exp)
    2. Define g(x) = 1 / f(1/x)
    3. Let h(x) = g(1+x) g(1−x).
    4. Zero out x∉(−1,1)
    5. Scale, shift, etc

In this post I’ll give a quick asymptotic proof that the construction above works.

Let a positive integer n be given and define g(x) to be zero for negative x. We’ll show that if f grows faster than xn. then g is n times differentiable at 0.

As x → ∞, f(x) is eventually bounded below by a function growing faster than xn. And so as x → 0, f(1/x) grows faster than xn and 1/f(1/x) goes to zero faster than xn, and so its nth derivative is zero.

It follows that g(1 + x) is n times differentiable at -1 and g(1 – x) is n times differentiable at 1. So h is n times differentiable at -1 and 1. The function h is positive on the open interval (-1, 1)  and zero outside. Our choice of n was arbitrary, so h is infinitely differentiable, and so h is a bump function. We could shift and scale h to make it a bump function on any other finite interval.

Discussion

When I was a student, I would have called this kind of proof hand waving. I’d want to see every inequality made explicit: there exists some M > 0 such that for x > M …. Now I find arguments like the one above easier to follow and more convincing. I imagine if a lecturer gives a proof with all the inequalities spelled out, he or she is probably thinking about something like the proof above and expanding the asymptotic argument on the fly.

Note that a slightly more general theorem falls out of the proof. Our goal was to show if f grows faster than every polynomial, then g and h are infinitely differentiable. But along the way we proved, for example, that if f eventually grows like x7 then g and h are six-times differentiable.

In fact, let’s look at the case f(x) = x7.

    f[x_] := x^7
    g[x_] := If[x > 0, 1/ f[1/x], 0]
    h[x_] := g[x + 1] g[1 - x]
    Plot[h[x], {x, -1.5, 1.5}]

This produces the following plot.

Just looking at the plot, h looks smooth; it’s plausible that it has six derivatives. It appears h is zero outside [-1, 1] and h is positive over at least part of [-1, 1]. If you look at the Mathematica code you can convince yourself that h really is positive on the entire interval open interval (-1, 1), though it is very small as it approaches either end.

Related posts

Polynomial analog of the Collatz conjecture

Posted on by John

The Collatz conjecture, a.k.a. the 3n + 1 problem, a.k.a. the hailstone conjecture, asks whether the following sequence always terminates.

Start with a positive integer n.

  1. If n is even, set n ← n /2. Otherwise n ← 3n + 1.
  2. If n = 1, stop. Otherwise go back to step 1.

The Collatz conjecture remains an unsolved problem, though there has been progress toward a proof. Some people, however, are skeptical whether the conjecture is true.

This post will look at a polynomial analog of the Collatz conjecture. Instead of starting with a positive integer, we start with a polynomial with coefficients in the integers mod m.

If the polynomial is divisible by x, then divide by x. Otherwise, multiply by (x + 1) and add 1. Here x is analogous to 2 and (x + 1) is analogous to 3 in the (integer) Collatz conjecture.

Here is Mathematica code to carry out the polynomial Collatz operation.

    c[p_, m_] := 
        PolynomialMod[
            If[ (p /. x -> 0) == 0, 
                 p/x, 
                 (x + 1) p + 1
            ], 
            m
        ]

If m = 2, the process always converges. In fact, it converges in at most n² + 2n steps where n is the degree of the polynomial [1].

Here’s an example starting with the polynomial x7 + x3 + 1.

    Nest[c[#, 2] &, x^7 + x^3 + 1, 15]

This returns 1, and so in this instance 15 iterations are enough.

If m = 3, however, the conjecture is false. In [1] the authors report that the sequence starting with x² + 1 is periodic with period 6.

The following code produces the sequence of values.

    NestList[c[#, 3] &, x^2 + 1, 6]

This returns the sequence

  • 1 + x2
  • 2 + x + x2 + x3
  • 2 x2 + 2 x3 + x4
  • 2 x + 2 x2 + x3
  • 2 + 2 x + x2
  • x + x3
  • 1 + x2

Related posts

[1] Kenneth Hicks, Gary L. Mullen, Joseph L. Yucas and Ryan Zavislak. A Polynomial Analogue of the 3n + 1 Problem. The American Mathematical Monthly, Vol. 115, No. 7. pp. 615-622.

Simple derivation of exponential approximation

Posted on by John

I was watching one of Brian Douglas’ videos on control theory (Discrete Control #5) and ran into a simple derivation of an approximation I presented earlier.

Back in April I wrote several post on simple approximations for log, exp, etc. In this post I gave an approximation for the exponential function:

\exp(x) \approx \frac{2 + x}{2 - x}

The control theory video arrives at the same approximation as follows.

\begin{align*} \exp(x) &= \exp(x/2)\, \exp(x/2) \\ &= \frac{\exp(x/2)}{\exp(-x/2)} \\ &\approx \frac{1 + x/2}{1 - x/2} \\ &= \frac{2 + x}{2-x} \end{align*}

As I believe I’ve suggested before here, in a derivation like the one above, where you have mostly equalities and one or two approximations, pay special attention to the approximation steps. The approximation step above uses a first order Taylor approximation in the numerator and denominator.

The plot below shows that the approximation above (the bilinear approximation) is more accurate than doing a single Taylor approximation, approximating exp(x) by 1 + x (linear approximation).

exp, linear approx, bilinear approx

Here’s a plot focusing on the error in the bilinear and linear approximations.

error in linear and bilinear approximations to exp

The bilinear approximation is hard to tell from 0 in the plot above for x up to 0.5.

The derivation above is simple, but why is the result so good? An explanation in terms of Padé approximation is given here.

Hebrew letters spotted in applied math

Posted on by John

Math and physics use Greek letters constantly, but seldom do they use letters from any other alphabet.

The only Cyrillic letter I recall seeing in math is sha (Ш, U+0428) for the so-called Dirc comb distribution.

One Hebrew letter is commonly used in math, and that’s aleph (א, U+05D0). Aleph is used fairly often, but other Hebrew letters are much rarer. If you see any other Hebrew letter in math, it’s very likely to be one of the next three letters: beth (ב, U+05D1), gimel (ג, U+05D2), or dalet (ד, U+05D3).

To back up this claim, basic LaTeX only has a command for aleph (unsurprisingly, it’s \aleph). AMS-LaTeX adds the commands \beth, \gimel, and \daleth, but no more. Those are the only Hebrew letters you can use in LaTeX without importing a package or using XeTeX so you can use Unicode symbols.

Not only are Hebrew letters rare in math, the only area of math that uses them at all is set theory, where they are used to represent transfinite numbers.

So in short, if you see a Hebrew letter in math, it’s overwhelmingly likely to be in set theory, and it’s very likely to be aleph, or possibly beth, gimel, or dalet.

But today I was browsing through Morse and Feschbach and was very surprised to see the following on page 324.

gimel = lambda ayin + mu yod + mu yod star

I’ve never seen a Hebrew letter in applied math, and I’ve never seen ayin (ע, U+05E2) or yod (י, U+05D9) used anywhere in math.

In context, the authors had used Roman letters, Fraktur letters, and Greek letters and so they’d run out of alphabets. The entity denoted by gimel is related to a tensor the authors denoted with g, so presumably they used the Hebrew letter that sounds like “g”. But I have no idea why they chose ayin or yod.

Related posts

Inverse Gray code

Posted on by John

The previous post looked at Gray code, a way of encoding digits so that the encodings of consecutive integers differ in only bit. This post will look at how to compute the inverse of Gray code.

The Gray code of a non-negative integer n is given by

    def gray(n):
        return n ^ (n >> 1)

Bit-level operations

In case you’re not familiar with the notation, the >> operator shifts the bits of its argument. The code above shifts the bits of n one place to the right. In the process, the least significant bit falls off the end. We could replace n >> 1 with n // 2 if we like, i.e. integer division by 2, rounding down if n is odd. The ^ operator stands for XOR, exclusive OR. A bit of x ^ y is 0 if both corresponding bits in x and y are the same, and 1 if they are different.

Computing the inverse

The inverse of Gray code is a more complicated. If we assume n < 232, then we can compute the inverse Gray code of n by

    def inverse_gray32(n):
        assert(0 <= n < 2**32) n = n ^ (n >> 1)
        n = n ^ (n >> 2)
        n = n ^ (n >> 4)
        n = n ^ (n >> 8)
        n = n ^ (n >> 16)
        return n

For n of any size, we can compute its inverse Gray code by

    def inverse_gray(n):
        x = n
        e = 1
        while x:
            x = n >> e
            e *= 2
            n = n ^ x
        return n

If n is a 32-bit integer, inverse_gray32 is potentially faster than inverse_gray because of the loop unrolling.

Plots

Here’s a plot of the Gray code function and its inverse.

Proof via linear algebra

How do we know that what we’re calling the inverse Gray code really is the inverse? Here’s a proof for 32-bit integers n.

    def test_inverse32():
        for i in range(32):
            x = 2**i
            assert(inverse_gray32(gray(x)) == x)
            assert(gray(inverse_gray32(x)) == x)

How is that a proof? Wouldn’t you need to try all possible 32-bit integers if you wanted a proof by brute force?

If we think of 32-bit numbers as vectors in a 32-dimensional vector space over the binary field, addition is defined by XOR. So XOR is linear by definition. It’s easy to see that shifts are also linear, and the composition of linear functions is linear. This means that gray and inverse_gray32 are linear transformations. If the two linear transformations are inverses of each other on the elements of a basis, they are inverses everywhere. The unit basis vectors in our vector space are simply the powers of 2.

Matrix representation

Because Gray code and its inverse are linear transformations, they can be defined by matrix multiplication (over the binary field). So we could come up with 32 × 32 binary matrices for Gray code and its inverse. Matrix multiplication would give us a possible, but inefficient, way to implement these functions. Alternatively, you could think of the code above as clever ways to implement multiplication by special matrices very efficiently!

OK, so what are the matrices? For n-bit numbers, the matrix giving the Gray code transformation has dimension n by n. It has 1’s on the main diagonal, and on the diagonal just below the main diagonal, and 0s everywhere else. The inverse of this matrix, the matrix for the inverse Gray code transformation, has 1s on the main diagonal and everywhere below.

Here are the matrices for n = 4.

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}

The matrix on the left is for Gray code, the next matrix is for inverse Gray code, and the last matrix is the identity. NB: The equation above only holds when you’re working over the binary field, i.e. addition is carried out mod 2, so 1 + 1 = 0.

To transform a number, represent it as a vector of length n, with the least significant in the first component, and multiply by the appropriate matrix.

Relation to popcount

It’s easy to see by induction that a number is odd if and only if its Gray code has an odd number of 1. The number 1 is its own Gray code, and as we move from the Gray code of n to the Gray code of n+1 we change one bit, so we change the parity of the the number of 1s.

There’s a standard C function popcount that counts the number of 1’s in a number’s binary representation, and the last bit of the popcount is the parity of the number of 1s. I blogged about this before here. If you look at the code at the bottom of that post, you’ll see that it’s the same as gray_inverse32.

The code in that post works because you can compute whether a word has an odd or even number of 1s by testing whether it is the Gray code of an odd or even number.