Peaks of Sinc

Posted on 18 January 2021 by John

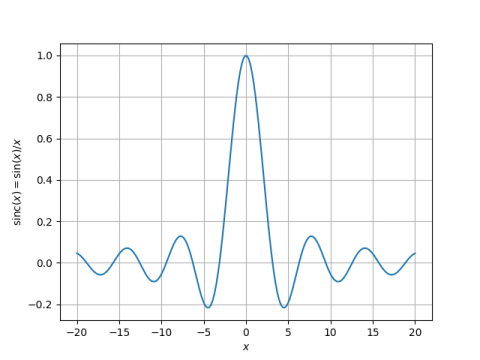
Yesterday I wrote two posts about finding the peaks of the sinc function. Both focused on numerical methods, the first using a contraction mapping and the second using Newton’s method. This post will focus on the locations of the peaks rather than ways of computing them.

The first post included this discussion of the peak locations.

The peaks of sin(x)/x are approximately at the same positions as sin(x), and so we use (2n + 1/2)π as our initial guess. In fact, all our peaks will be a little to the left of the corresponding peak in the sine function because dividing by x pulls the peak to the left. The larger x is, the less it pulls the root over.

This post will refine the observation above. The paragraph above suggests that for large n, the nth peak is located at approximately (2n + 1/2)π. This is a zeroth order asymptotic approximation. Here we will give a first order asymptotic approximation.

For a fixed positive n, let

θ = (2n + 1/2)π

and let

x = θ + ε

be the location of the nth peak. We will improve or approximation of the location of x by estimating ε.

As described in the first post in this series, setting the derivative of the sinc function to zero says x satisfies

x cos x – sin x = 0.

Therefore

(θ + ε) cos(θ + ε) = sin(θ + ε)

Applying the sum-angle identities for sine and cosine shows

(θ + ε) (cos θ cos ε – sin θ sin ε) = sin θ cos ε + cos θ sin ε

Now sin θ = 1 and cos θ = 0, so

-(θ + ε) sin ε = cos ε.

tan ε = -1/(θ + ε).

So far our calculations are exact. You could, for example, solve the equation above for ε using a numerical method. But now we’re going to make a couple very simple approximations [1]. On the left, we will approximate tan ε with ε. On the right, we will approximate ε with 0. This gives us

ε ≈ -1/θ = -1/(2n + 1/2)π.

This says the nth peak is located at approximately

θ – 1/θ

where θ = (2n + 1/2)π. This refines the earlier statement “our peaks will be a little to the left of the corresponding peak in the sine function.” As n gets larger, the term we subtract off gets smaller. This makes the statement above “The larger x is, the less it pulls the root over” more precise.

Now let’s see visually how well our approximation works. The graph below plots the error in approximating the nth peak location by θ and by θ – 1/θ.

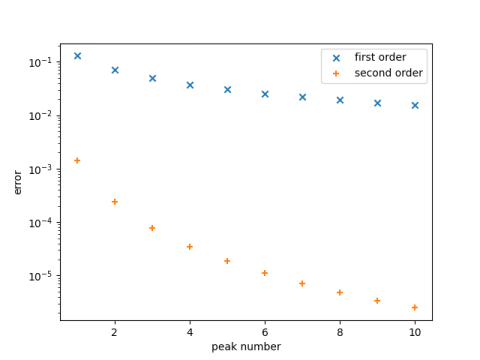
Note the log scale. The error in approximating the location of the 10th peak by 20.5π is between 0.1 and 0.01, and the error in approximating the location by 20.5π – 1/20.5π is approximately 0.000001.

[1] As pointed out in the comments, you could a slightly better approximation by not being so simple. Instead of approximating 1/(θ + ε) by 1/θ you could use 1/θ – ε/θ² and solve for ε.

Rate of convergence for Newton’s method

Posted on 17 January 2021 by John

In the previous post I looked at the problem of finding the peaks of the sinc function.

In this post we use this problem to illustrate how two formulations of the same problem can behave very differently with Newton’s method.

The previous post mentioned finding the peaks by solving either

x cos x – sin x = 0

or equivalently

tan x – x = 0

It turns out that the former is much better suited to Newton’s method. Newton’s method applied to the first equation will converge quickly without needing to start particularly close to the root. Newton’s method applied to the second equation will fail to converge at all unless the method beings close to the root, and even then the method may not be accurate.

Here’s why. The rate of convergence in solving

f(x) = 0

with Newton’s method is determined by the ratio of the second derivative to the first derivative

| f ‘ ‘ (x) / f ‘ (x) |

near the root.

Think of the second derivative as curvature. Dividing by the first derivative normalizes the scale. So convergence is fast when the curvature relative to the scale is small. Which makes sense intuitively: When a function is fairly straight, Newton’s method zooms down to the root. When a function is more curved, Newton’s method requires more steps.

The following table gives the absolute value of the ratio of the second derivative to the first derivative at the first ten peaks, using both equations. The bound on the error in Newton’s method is proportional to this ratio.

    |------+------------+------------|
    | peak | Equation 1 | Equation 2 |
    |------+------------+------------|
    |    1 |      0.259 |       15.7 |
    |    2 |      0.142 |       28.3 |
    |    3 |      0.098 |       40.8 |
    |    4 |      0.075 |       53.4 |
    |    5 |      0.061 |       66.0 |
    |    6 |      0.051 |       78.5 |
    |    7 |      0.044 |       91.1 |
    |    8 |      0.039 |      103.7 |
    |    9 |      0.034 |      116.2 |
    |   10 |      0.031 |      128.8 |
    |------+------------+------------|

The error terms are all small for the first equation, and they get smaller as we look at peaks further from the origin. The error terms for the second equation are all large, and get larger as we look at peaks further out.

For the third and final post in this series, see Peaks of Sinc.

Reverse iteration root-finding

Posted on 17 January 2021 by John

The sinc function is defined by

sinc(x) = sin(x)/x.

This function comes up constantly in signal processing. Here’s a plot.

We would like to find the location of the function’s peaks. Let’s focus first on the first positive peak, the one that’s somewhere between 5 and 10. Once we can find that one, the rest will be easy.

If you take the derivative of sinc and set it to zero, you find that the peaks must satisfy

x cos x – sin x = 0

which means that

tan x = x.

So our task reduces to finding the fixed points of the tangent function. One way to find fixed points is simply to iterate the function. We pick a starting point near the peak we’re after, then take its tangent, then take the tangent of that, etc.

The peak appears to be located around 7.5, so we’ll use that as a starting point. Then iterates of tangent give

     2.7060138667726910
    -0.4653906051625444
    -0.5021806478408769
    -0.5491373258198057
    -0.6119188887713993
    -0.7017789436750164
    -0.8453339618848119
    -1.1276769374114777
    -2.1070512803092996
     1.6825094538261074

That didn’t work at all. That’s because tangent has derivative larger than 1, so it’s not a contraction mapping.

The iterates took us away from the root we were after. This brings up an idea: is there some way to iterate a negative number of times? Well, sorta. We can run our iteration backward.

Instead of solving

tan x = x

we could equivalently solve

arctan x = x.

Since iterating tangent pushes points away, iterating arctan should bring them closer. In fact, the derivative of arctan is less than 1, so it is a contraction mapping, and we will get a fixed point.

Let’s start again with 7.5 and iterate arctan. This quickly converges to the peak we’re after.

    7.721430101677809
    7.725188823982156
    7.725250798474231
    7.725251819823800
    7.725251836655669
    7.725251836933059
    7.725251836937630
    7.725251836937706
    7.725251836937707
    7.725251836937707

There is a little complication: we have to iterate the right inverse tangent function. Since tangent is periodic, there are infinitely many values of x that have a particular tangent value. The arctan function in NumPy returns a value between -π/2 and π/2. So if we add 2π to this value, we get values in an interval including the peak we’re after.

Here’s how we can find all the peaks. The peak at 0 is obvious, and by symmetry we only need to find the positive peaks; the nth negative peak is just the negative of the nth positive peak.

The peaks of sin(x)/x are approximately at the same positions as sin(x), and so we use (2n + 1/2)π as our initial guess. In fact, all our peaks will be a little to the left of the corresponding peak in the sine function because dividing by x pulls the peak to the left. The larger x is, the less it pulls the root over.

The following Python code will find the nth positive peak of the sinc function.

    def iterate(n, num_iterates = 6):
        x = (2*n + 0.5)*np.pi
        for _ in range(num_iterates):
            x = np.arctan(x) + 2*n*np.pi
    return x

My next post will revisit the problem in this post using Newton’s method.

Symplectic Euler

Posted on 12 September 2020 by John

This post will look at simple numerical approaches to solving the predator-prey (Lotka-Volterra) equations. It turns out that the simplest approach does poorly, but a slight variation does much better.

Following [1] we will use the equations

u‘ = u (v – 2)
v‘ = v (1 – u)

Here u represents the predator population over time and v represents the prey population. When the prey v increase, the predators u increase, leading to a decrease in prey, which leads to a decrease in predators, etc. The exact solutions are periodic.

Euler’s method replaces the derivatives with finite difference approximations to compute the solution in increments of time of size h. The explicit Euler method applied to our example gives

u(t + h) = u(t) + h u(t) (v(t) – 2)
v(t + h) = v(t) + h v(t) (1 – u(t)).

The implicit Euler method gives

u(t + h) = u(t) + h u(t + h) (v(t + h) – 2)
v(t + h) = v(t) + h v(t + h) (1 – u(t + h)).

This method is implicit because the unknowns, the value of the solution at the next time step, appear on both sides of the equation. This means we’d either need to do some hand calculations first, if possible, to solve for the solutions at time t + h, or use a root-finding method at each time step to solve for the solutions.

Implicit methods are more difficult to implement, but they can have better numerical properties. See this post on stiff equations for an example where implicit Euler is much more stable than explicit Euler. I won’t plot the implicit Euler solutions here, but the implicit Euler method doesn’t do much better than the explicit Euler method in this example.

It turns out that a better approach than either explicit Euler or implicit Euler in our example is a compromise between the two: use explicit Euler to advance one component and use implicit Euler on the other. This is known as symplectic Euler for reasons I won’t get into here but would like to discuss in a future post.

If we use explicit Euler on the predator equation but implicit Euler on the prey equation we have

u(t + h) = u(t) + h u(t) (v(t + h) – 2)
v(t + h) = v(t) + h v(t + h) (1 – u(t)).

Conversely, if we use implicit Euler on the predator equation but explicit Euler on the prey equation we have

u(t + h) = u(t) + h u(t + h) (v(t) – 2)
v(t + h) = v(t) + h v(t) (1 – u(t + h)).

Let’s see how explicit Euler compares to either of the symplectic Euler methods.

First some initial setup.

    import numpy as np

    h  = 0.08  # Step size
    u0 = 6     # Initial condition
    v0 = 2     # Initial condition
    N  = 100   # Numer of time steps

    u = np.empty(N)
    v = np.empty(N)
    u[0] = u0
    v[0] = v0

Now the explicit Euler solution can be computed as follows.

    for n in range(N-1):
        u[n+1] = u[n] + h*u[n]*(v[n] - 2)
        v[n+1] = v[n] + h*v[n]*(1 - u[n])

The two symplectic Euler solutions are

    
    for n in range(N-1):
        v[n+1] = v[n]/(1 + h*(u[n] - 1))
        u[n+1] = u[n] + h*u[n]*(v[n+1] - 2)

and

    for n in range(N-1):
        u[n+1] = u[n] / (1 - h*(v[n] - 2))
        v[n+1] = v[n] + h*v[n]*(1 - u[n+1])

Now let’s see what our solutions look like, plotting (u(t), v(t)). First explicit Euler applied to both components:

And now the two symplectic methods, applying explicit Euler to one component and implicit Euler to the other.

Next, let’s make the step size 10x smaller and the number of steps 10x larger.

Now the explicit Euler method does much better, though the solutions are still not quite periodic.

The symplectic method solutions hardly change. They just become a little smoother.

Conceptual vs Numerical

Posted on 3 August 2020 by John

One of the things that makes numerical computation interesting is that it often reverses the usual conceptual order of things, using advanced math to compute things that are introduced earlier.

Here’s an example I recently ran across [1]. The hyperbolic functions are defined in terms of the exponential function:

$\begin{align*} \sinh(x) &= \frac{\exp(x) - \exp(-x)}{2} \\ \cosh(x) &= \frac{\exp(x) + \exp(-x)}{2} \\ \tanh(x) &= \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} \\ \end{align*}$

But it may be more efficient to compute the exponential function in terms of hyperbolic functions. Specifically,

$\exp(x) = \sinh(x) + \sqrt{\sinh(x)^2 + 1}$

Why would you want to compute the simple thing on the left in terms of the more complicated thing on the right? Because hyperbolic sine is an odd function. This means that half its power series coefficients are zero: an odd function only has odd powers in its power series.

Suppose you need to compute the exponential function in an environment where you only have a limited number of registers to store constants. You can get more accuracy out of the same number of registers by using them to store coefficients in the power series for hyperbolic sine than for exp.

If we store n coefficients for sinh, we can include powers of x up to 2n – 1. And since the coefficient of x²ⁿ is zero, the error in our Taylor approximation is O(x²ⁿ⁺¹). See this post for more on this trick.

If we stored n coefficients for exp, we could include powers of x up to n-1, and our error would be O(xⁿ).

To make things concrete, suppose n = 3 and x = 0.01. The error in the exp function would be on the order of 10^-6, but the error in the sinh function would be on the order of 10^-14. That is, we could almost compute exp to single precision and sinh to almost double precision.

(I’m glossing over a detail here. Would you really need to store, for example, the 1 coefficient in front of x in either series? For simplicity in the argument above I’ve implicitly said yes. Whether you’d actually need to store it depends on the details of your implementation.)

The error estimate above uses big-oh arguments. Let’s do an actual calculation to see what we get.

    from math import exp, sinh, sqrt
    
    def exp_taylor(x):
        return 1 + x + 0.5*x**2
    
    def sinh_taylor(x):
        return x + x**3/6 + x**5/120
    
    def exp_via_sinh(x):
        s = sinh_taylor(x)
        return s + sqrt(s*s + 1)
    
    def print_error(approx, exact):
        print(f"Computed: {approx}")
        print(f"Exact:    {exact}")
        print(f"Error:    {approx - exact}")
    
    x = 0.01
    approx1 = exp_taylor(x)
    approx2 = exp_via_sinh(x)
    exact   = exp(x)
    
    print("Computing exp directly:\n")
    print_error(approx1, exact)
    
    print()
    
    print("Computing exp via sinh:\n")
    print_error(approx2, exact)

This produces

    Computing exp directly:

    Computed: 1.0100500000000001
    Exact:    1.010050167084168
    Error:    -1.6708416783473012e-07

    Computing exp via sinh:

    Computed: 1.0100501670841682
    Exact:    1.010050167084168
    Error:    2.220446049250313e-16

Our errors are roughly what we expected from our big-oh arguments.

Leapfrog integrator

Posted on 13 July 2020 by John

The so-called “leapfrog” integrator is a numerical method for solving differential equations of the form

where x is a function of t. Typically x is position and t is time.

This form of equation is common for differential equations coming from mechanical systems. The form is more general than it may seem at first. It does not allow terms involving first-order derivatives, but these terms can often be eliminated via a change of variables. See this post for a way to eliminate first order terms from a linear ODE.

The leapfrog integrator is also known as the Störmer-Verlet method, or the Newton-Störmer-Verlet method, or the Newton-Störmer-Verlet-leapfrog method, or …

The leapfrog integrator has some advantages over, say, Runge-Kutta methods, because it is specialized for a particular (but important) class of equations. For one thing, it solves the second order ODE directly. Typically ODE solvers work on (systems of) first order equations: to solve a second order equation you turn it into a system of first order equations by introducing the first derivative of the solution as a new variable.

For another thing, it is reversible: if you advance the solution of an ODE from its initial condition to some future point, make that point your new initial condition, and reverse time, you can step back to exactly where you started, aside from any loss of accuracy due to floating point; in exact arithmetic, you’d return to exactly where you started.

Another advantage of the leapfrog integrator is that it approximately conserves energy. The leapfrog integrator could perform better over time compared to a method that is initially more accurate.

Here is the leapfrog method in a nutshell with step size h.

$\begin{align*} x_{i+1} &= x_i + v_i h + \frac{1}{2} f(x_i) h^2 \\ v_{i+i} &= v_i + \frac{1}{2}\left(f(x_i) + f(x_{i+1})\right) h \end{align*}$

And here’s a simple Python demo.

    import numpy as np
    import matplotlib.pyplot as plt
    
    # Solve x" = f(x) using leapfrog integrator
    
    # For this demo, x'' + x = 0
    # Exact solution is x(t) = sin(t)
    def f(x):
        return -x
    
    k = 5               # number of periods
    N = 16              # number of time steps per period
    h = 2*np.pi/N       # step size
    
    x = np.empty(k*N+1) # positions
    v = np.empty(k*N+1) # velocities
    
    # Initial conditions
    x[0] = 0
    v[0] = 1
    anew = f(x[0])
    
    # leapfrog method
    for i in range(1, k*N+1):
        aold = anew
        x[i] = x[i-1] + v[i-1]*h + 0.5*aold*h**2
        anew = f(x[i])
        v[i] = v[i-1] + 0.5*(aold + anew)*h

Here’s a plot of the solution over five periods.

There’s a lot more I hope to say about the leapfrog integrator and related methods in future posts.

NASA’s favorite ODE solver

Posted on 16 June 2020 by John

NASA’s Orbital Flight Handbook, published in 1963, is a treasure trove of technical information, including a section comparing the strengths and weaknesses of several numerical methods for solving differential equations.

The winner was a predictor-corrector scheme known as Gauss-Jackson, a method I have not heard of outside of orbital mechanics, but one apparently particularly well suited to NASA’s needs.

The Gauss-Jackson second-sum method is strongly recommended for use in either Encke or Cowell [approaches to orbit modeling]. For comparable accuracy, it will allow step-sizes larger by factors of four or more than any of the forth order methods. … As compared with unsummed methods of comparable accuracy, the Gauss-Jackson method has the very important advantage that roundoff error growth is inhibited. … The Gauss-Jackson method is particularly suitable on orbits where infrequent changes in the step-size are necessary.

Here is a table summarizing the characteristics of each of the solvers.

Notice that Gauss-Jackson is the only method whose roundoff error accumulation is described as “excellent.”

A paper from 2004 [1] implies that the Gauss-Jackson method was still in use at NASA at the time of writing.

The Gauss-Jackson multi-step predictor-corrector method is widely used in numerical integration problems for astrodynamics and dynamical astronomy. The U.S. space surveillance centers have used an eighth-order Gauss-Jackson algorithm since the 1960s.

I could imagine a young hotshot explaining to NASA why they should use some other ODE solver, only to be told that the agency had already evaluated the alternatives half a century ago, and that the competitors didn’t have the same long-term accuracy.

ODE solver landscape

Posted on 12 June 2020 by John

Many methods for numerically solving ordinary differential equations are either Runge-Kutta methods or linear multistep methods. These methods can either be explicit or implicit.

The table below shows the four combinations of these categories and gives some examples of each.

$\begin{tabular}{|l|ll|} \hline & Runge-Kutta & Linear multistep\\ \hline Explicit & ERK & Adams-Bashforth\\ Implicit & (S)DIRK & Adams-Moulton, BDF\\ \hline \end{tabular}$

Runge-Kutta methods advance the solution of a differential equation one step at a time. That is, these methods approximate the solution at the next time step using only the solution at the current time step and the differential equation itself.

Linear multistep methods approximate the solution at the next time step using the computed solutions at the latest several time steps.

Explicit methods express the solution at the next time step as an explicit function of other information, not including the solution itself. The solution at the next time step appears on only one side of the equations.

Implicit methods express the solution at the next time step as a function of other information including the solution itself. The solution at the next time step appears on both sides of the equations. Additional work needs to be done to solve for the solution.

More on explicit vs implicit methods here.

In the table above, ERK stands for, not surprisingly, explicit Runge-Kutta methods. DIRK stands for diagonally implicit Runge-Kutta. SDIRK stands for singly diagonally implicit Runge-Kutta. BDF stands for backward difference formulas.

How to compute the square root of a complex number

Posted on 9 June 2020 by John

Suppose you’re given a complex number

z = x + iy

and you want to find a complex number

w = u + iv

such that w² = z. If all goes well, you can compute w as follows:

ℓ = √(x² + y²)
u = √((ℓ + x)/2)
v = sign(y) √((ℓ – x)/2).

For example, if z = 5 + 12i, then ℓ = 13, u = 3, and v = 2. A quick calculation confirms

(3 + 2i)² = 5 + 12i.

(That example worked out very nicely. More on why in the next post.)

Note that ℓ ≥ |x|, and so the square roots above have non-negative arguments.

Numerical issues

I said “if all goes well” above because in floating point arithmetic, various things could go wrong. In [1], the authors point out that x² + y² could overflow. They give a more complicated algorithm that addresses the problem of overflow, and they reference a paper with an even more complicated algorithm to cover all the corner cases — NaNs, infinities, etc.

If you have access to a hypot function, it will let you compute √(x² + y²) without overflow. If you don’t have access to a hypot function, you can roll your own quickly using the algorithm here.

This may seem unnecessary. Why would you need to worry about overflow? And why would you have access to a real square root function but not a complex square root function?

If you’re using standard 64-bit floating point numbers, the hypotenuse calculation is not going to overflow as long as your arguments are less than 10¹⁵⁴, and you can use the function csqrt from complex.h.

But if you’re using a 16-bit float or even an 8-bit float, overflow is an ever-present concern, and you might not have the math library support you’re accustomed to.

[1] Jean-Michel Muller et al. Handbook of Floating Point Arithmetic.

Accurately computing a 2×2 determinant

Posted on 31 May 2020 by John

The most obvious way to compute the determinant of a 2×2 matrix can be numerically inaccurate. The biggest problem with computing ad – bc is that if ad and bc are approximately equal, the subtraction could lose a lot of precision. William Kahan developed an algorithm for addressing this problem.

Fused multiply-add (FMA)

Kahan’s algorithm depends on a fused multiply-add function. This function computes xy + z using one rounding operation at the end, where the direct approach would use two.

In more detail, the fused multiply-add behaves as if it takes its the floating point arguments x, y, and z and lifts them to the Platonic realm of real numbers, calculates xy + z exactly, and then brings the result back to the world of floating point numbers. The true value of xy + z may not have an exact representation in the floating point world, and so in general it will be necessary to round the result.

The direct way of computing xy + z would behave as if it first lifts x and y to the Platonic realm, computes xy exactly, then pushes the result back down to the floating point world, rounding the result. Then it takes this rounded version of xy back up to the Platonic realm, possibly to a different value than before, and pushes z up, adds the two numbers, then pushes the sum back down to the world of floating point.

You can get more accuracy if you avoid round trips back and forth to the Platonic realm. If possible, you’d like to push everything up to the Platonic realm once, do as much work as you can up there, then come back down once. That’s what fused multiply-add does.

Kahan’s determinant algorithm

Here is Kahan’s algorithm for computing ad – bc for floating point numbers.

w = RN(bc)
e = RN(w – bc)
f = RN(ad – w)
x = RN(f + e)

The function RN computes its argument exactly, then rounds the result to the nearest floating point value, rounding to even in case of a tie. (This is the default rounding mode for compilers like gcc, so the C implementation of the algorithm will directly follow the more abstract specification above.)

If there were no rounding we would have

w = bc
e = w – bc = 0
f = ad – w = ad – bc
x = f + e = ad – bc + 0 = ad – bc

But of course there is rounding, and so Kahan’s steps that seem redundant are actually necessary and clever. In floating point arithmetic, e is not zero, but it does exactly equal w – bc. This is important to why the algorithm works.

Here is a C implementation of Kahan’s algorithm and a demonstration of how it differs from the direct alternative.

    #include <math.h>
    #include <stdio.h>
    
    double naive_det(double a, double b, double c, double d) {
        return a*d - b*c;
    }
    
    double kahan_det(double a, double b, double c, double d) {
        double w = b*c;
        double e = fma(-b, c, w);
        double f = fma(a, d, -w);
        return (f+e);
    }
    
    int main() {
        double a = M_PI;
        double b = M_E;
        double c = 355.0 / 113.0;
        double d = 23225.0 / 8544.0;
    
        printf("Naive: %15.15g\n", naive_det(a, b, c, d));
        printf("Kahan: %15.15g\n", kahan_det(a, b, c, d));
    }

The values of c and d were chosen to be close to M_PI and M_E so that the naive computation of the determinant would less accurate. See these post on rational approximations to π and rational approximations to e.

The code above prints

    Naive: -7.03944087021569e-07
    Kahan: -7.03944088015194e-07

How do we know that Kahan’s result is accurate? Careful analysis of Kahan’s algorithm in [1] gives bounds on its accuracy. In particular, the absolute error is bounded by 1.5 ulps, units of least precision.

Numerical analysis

Peaks of Sinc

Rate of convergence for Newton’s method

Related posts

Reverse iteration root-finding

Symplectic Euler

More differential equations posts

Conceptual vs Numerical

More numerical analysis posts

Leapfrog integrator

More on ODE solvers