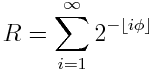SymPy

Alternating sums of factorials

Posted on by John

Richard Guy’s Strong Law of Small Numbers says

There aren’t enough small numbers to meet the many demands made of them.

In his article by the same name [1] Guy illustrates his law with several examples of patterns that hold for small numbers but eventually fail. One of these examples is

3! − 2! + 1! = 5

4! − 3! + 2! − 1! = 19

5! − 4! + 3! − 2! + 1! = 101

6! − 5! + 4! − 3! + 2! − 1! = 619

7! − 6! + 5! − 4! + 3! − 2! + 1! = 4421

8! − 7! + 6! − 5! + 4! − 3! + 2! − 1! = 35899

If we let f(n) be the alternating factorial sum starting with n, f(n) is prime for n = 3, 4, 5, 6, 7, 8, but not for n = 9. So the alternating sums aren’t all prime. Is f(n) usually prime? f(10) is, so maybe 9 is the odd one. Let’s write a code to find out.

    from sympy import factorial, isprime

    def altfact(n):
        sign = 1
        sum = 0
        while n > 0:
            sum += sign*factorial(n)
            sign *= -1
            n -= 1
        return sum

    numprimes = 0
    for i in range(3, 1000):
        if isprime( altfact(i) ):
            print(i)
            numprimes += 1
    print(numprimes)

You could speed up this code by noticing that

    altfact(n+1) = factorial(n+1) - altfact(n)

and tabulating the values of altfact. The code above corresponds directly to the math, though it takes a little while to run.

So it turns out the alternating factorial sum is only prime for 15 values less than 1000. In addition to the values of n mentioned above, the other values are 15, 19, 41, 59, 61, 105, 160, and 601.

* * *

[1] The Strong Law of Small Numbers, Richard K. Guy, The American Mathematical Monthly, Vol. 95, No. 8 (Oct., 1988), pp. 697-712.

Last digits of Fibonacci numbers

Posted on by John

If you write out a sequence of Fibonacci numbers, you can see that the last digits repeat every 60 numbers.

The 61st Fibonacci number is 2504730781961. The 62nd is 4052739537881. Since these end in 1 and 1, the 63rd Fibonacci number must end in 2, etc. and so the pattern starts over.

It’s not obvious that the cycle should have length 60, but it is fairly easy to see that there must be a cycle. There are only 10*10 possibilities for two consecutive digits. Since the Fibonacci numbers are determined by a two-term recurrence, and since the last digit of a sum is determined by the sum of the last digits, the sequence of last digits must repeat eventually. Here “eventually” means after at most 10*10 terms.

Replace “10” by any other base in the paragraph above to show that the sequence of last digits must be cyclic in any base. In base 16, for example, the period is 24. In hexadecimal notation the 25th Fibonacci number is 12511 and the 26th is 1DA31, so the 27th must end in 2, etc.

Here’s a little Python code to find the period of the last digits of Fibonacci numbers working in any base b.

from sympy import fibonacci as f

def period(b):
    for i in range(1, b*b+1):
        if f(i)%b == 0 and f(i+1)%b == 1:
            return(i)

This shows that in base 100 the period is 300. So in base 10 the last two digits repeat every 300 terms.

The period seems to vary erratically with base as shown in the graph below.

Related: Applied number theory

Numerators of harmonic numbers

Posted on by John

Harmonic numbers

The nth harmonic number, Hn, is the sum of the reciprocals of the integers up to and including n. For example,

H4 = 1 + 1/2 + 1/3 + 1/4 = 25/12.

Here’s a curious fact about harmonic numbers, known as Wolstenholme’s theorem:

For a prime p > 3, the numerator of Hp−1 is divisible by p2.

The example above shows this for p = 5. In that case, the numerator is not just divisible by p2, it is p2, though this doesn’t hold in general. For example, H10 = 7381/2520. The numerator 7381 is divisible by 112 = 121, but it’s not equal to 121.

Generalized harmonic numbers

The generalized harmonic numbers Hn,m are the sums of the reciprocals of the first n positive integers, each raised to the power m. Wolstenholme’s theorem also says something about these numbers too:

For a prime p > 3, the numerator of Hp−1,2 is divisible by p.

For example, H4,2 = 205/144, and the numerator is clearly divisible by 5.

Computing with Python

You can play with harmonic numbers and generalized harmonic numbers in Python using SymPy. Start with the import statement

from sympy.functions.combinatorial.numbers import harmonic

Then you can get the nth harmonic number with harmonic(n) and generalized harmonic numbers with harmonic(n, m).

To extract the numerators, you can use the method as_numer_denom to turn the fractions into (numerator, denominator) pairs. For example, you can create a list of the numerators of the first 10 harmonic numbers with

[harmonic(n).as_numer_denom()[0] for n in range(10)]

What about 0?

You might notice that harmonic(0) returns 0, as it should. The sum defining the harmonic numbers is empty in this case, and empty sums are defined to be zero.

 

Counting primitive bit strings

Posted on by John

A string of bits is called primitive if it is not the repetition of several copies of a smaller string of bits. For example, the 101101 is not primitive because it can be broken down into two copies of the string 101. In Python notation, you could produce 101101 by "101"*2. The string 11001101, on the other hand, is primitive. (It contains substrings that are not primitive, but the string as a whole cannot be factored into multiple copies of a single string.)

For a given n, let’s count how many primitive bit strings there are of length n. Call this f(n). There are 2n bit strings of length n, and f(n) of these are primitive. For example, there are f(12) primitive bit strings of length 12. The strings that are not primitive are made of copies of primitive strings: two copies of a primitive string of length 6, three copies of a primitive string of length 4, etc. This says

2^{12} = f(12) + f(6) + f(4) + f(3) + f(2) + f(1)

and in general

2^n = \sum_{d \mid n} f(d)

Here the sum is over all positive integers d that divide n.

Unfortunately this formula is backward. It gives is a formula for something well known, 2n, as a sum of things we’re trying to calculate. The Möbius inversion formula is just what we need to turn this formula around so that the new thing is on the left and sums of old things are on the right. It tells us that

f(n) = \sum_{d \mid n} \mu\left(\frac{n}{d}\right) 2^d

where μ is the Möbius function.

We could compute f(n) with Python as follows:

    from sympy.ntheory import mobius, divisors

    def num_primitive(n):
        return sum( mobius(n/d)*2**d for d in divisors(n) )

The latest version of SymPy, version 0.7.6, comes with a function mobius for computing the Möbius function. If you’re using an earlier version of SymPy, you can roll your own mobius function:

    from sympy.ntheory import factorint

    def mobius(n):
        exponents = factorint(n).values()
        lenexp = len(exponents)
        m = 0 if lenexp == 0 else max(exponents)
        return 0 if m > 1 else (-1)**lenexp

The version of mobius that comes with SymPy 0.7.6 may be more efficient. It could, for example, stop the factorization process early if it discovers a square factor.

Related: Applied number theory

Number theory determinant and SymPy

Posted on by John

Let σ(n) be the sum of the positive divisors of n and let gcd(a, b) be the greatest common divisor of a and b.

Form an n by n matrix M whose (i, j) entry is σ(gcd(i, j)). Then the determinant of M is n!.

The following code shows that the theorem is true for a few values of n and shows how to do some common number theory calculations in SymPy.

from sympy import gcd, divisors, Matrix, factorial

def f(i, j):
    return sum( divisors( gcd(i, j) ) )

def test(n):
    r = range(1, n+1)
    M = Matrix( [ [f(i, j) for j in r] for i in r] )
    return M.det() - factorial(n)

for n in range(1, 11):
    print( test(n) )

As expected, the test function returns zeros.

If we replace the function σ above by τ where τ(n) is the number of positive divisors of n, the corresponding determinant is 1. To test this, replace sum by len in the definition of f and replace factorial(n) by 1.

In case you’re curious, both results are special cases of the following more general theorem. I don’t know whose theorem it is. I found it here.

For any arithmetic function f(m), let g(m) be defined for all positive integers m by

g(m) = \sum_{d \,\mid \,m} \mu(d) f\left(\frac{m}{d}\right)

Let M be the square matrix of order n with ij element f(gcd(i, j)). Then

\det M = \prod_i^n g(j)

Here μ is the Möbius function. The two special cases above correspond to g(m) = m and g(m) = 1.

A prime-generating formula and SymPy

Posted on by John

Mills’ constant is a number θ such that the integer part of θ raised to a power of 3 is always a prime. We’ll see if we can verify this computationally with SymPy.

from sympy import floor, isprime
from sympy.mpmath import mp, mpf

# set working precision to 200 decimal places
mp.dps = 200

# Mills' constant http://oeis.org/A051021
theta = mpf("1.30637788386308069046861449260260571291678458515671364436805375996643405376682659882150140370119739570729")

for i in range(1, 7):
    n = floor(theta**3**i)
    print i, n, isprime(n)

Note that the line of code defining theta wraps Mill’s constant as a string and passes it as an argument to mpf. If we just wrote theta = 1.30637788386308… then theta would be truncated to an ordinary floating point number and most of the digits would be lost. Not that I did that in the first version of the code. :)

This code says that the first five outputs are prime but that the sixth is not. That’s because we are not using Mills’ constant to enough precision. The integer part of θ^3^6 is 85 digits long, and we don’t have enough precision to compute the last digit correctly.

If we use the value of Mills’ constant given here to 640 decimal places, and increase mp.dps to 1000, we can correctly compute the sixth term, but not the seventh.

Mill’s formula is just a curiosity with no practical use that I’m aware of, except possibly as an illustration of impractical formulas.

A magic square filled with consecutive primes

Posted on by John

In 1988 Martin Gardner offered a $100 prize for the first person to produce a magic square filled with consecutive primes. Later that year, Harry Nelson found 22 solutions using a Cray computer.

1,480,028,201 1,480,028,129 1,480,028,183
1,480,028,153 1,480,028,171 1,480,028,189
1,480,028,159 1,480,028,213 1,480,028,141

Gardner said that the square above is “almost certainly the one with the lowest constant possible for such a square.”

It’s easy to verify that the numbers above are consecutive primes. Here’s a little Python code for the job. The function nextprime(x, i) gives the next i primes after x. We call the function with x equal to one less than the smallest entry in the square and it prints out all the entries.

    from sympy import nextprime
    for i in range(1,10):
        print( nextprime(148028128, i) )

If you’re looking for more than a challenge, verify whether Gardner’s assertion was correct that the square above uses the smallest possible set of consecutive primes.

By the way, assuming Harry Nelson’s Cray was the Y-MP model that came out in 1988, here are its specs according to Wikipedia:

The Y-MP could be equipped with two, four or eight vector processors, with two functional units each and a clock cycle time of 6 ns (167 MHz). Peak performance was thus 333 megaflops per processor. Main memory comprised 128, 256 or 512 MB of SRAM.

Related: Magic squares from a knight’s tour and a king’s tour.

Golden strings and the rabbit constant

Posted on by John

Golden strings are analogous to Fibonacci numbers, except one uses concatenation rather than addition.

Start with s1 = “1” and s2 = “10”. Then define sn = sn-1 + sn-2 where “+” means string concatenation.

The first few golden strings are

  • “1”
  • “10”
  • “101”
  • “10110”
  • “10110101”
  • …

The length of sn is Fn+1, the n+1st Fibonacci number. Also, sn contains Fn 1’s and Fn-1 0’s. (Source: The Glorious Golden Ratio).

If we interpret the sn as the fractional part of a binary number, the sequence converges to the rabbit constant R = 0.7098034428612913…

It turns out that R is related to the golden ratio φ by

R = \sum_{i=1}^\infty 2^{-\lfloor i \phi \rfloor}

where ⌊i φ⌋ is the largest integer no greater than iφ.

Here’s a little Python code to print out the first few golden strings and an approximation to the rabbit constant.

    from mpmath import mp, fraction

    a = "1"
    b = "10"
    for i in range(10):
        b, a = b+a, b
        print(b)

    n = len(b)
    mp.dps = n
    denom = 2**n
    num = int(b, 2)

    rabbit = fraction(num, denom)
    print(rabbit)

Note that the code sets the number of decimal places, mp.dps, to the length of the string b. That’s because it takes up to n decimal places to exactly represent a rational number with denominator 2n.

Related posts

SymPy book

Posted on by John

There’s a new book on SymPy, a Python library for symbolic math.

The book is Instant SymPy Starter by Ronan Lamy. As far as I know, this is the only book just on SymPy. It’s only about 50 pages, which is nice. It’s not a replacement for the online documentation but just a quick start guide.

The online SymPy documentation is good, but I think it would be easier to start with this book. And although I’ve been using SymPy off and on for a while, I learned a few things from the book.

Need a 12-digit prime?

Posted on by John

You may have seen the joke “Enter any 12-digit prime number to continue.” I’ve seen it floating around as the punchline in several contexts.

So what do you do if you need a 12-digit prime? Here’s how to find the smallest one using Python.

    >>> from sympy import nextprime
    >>> nextprime(10**11)
    100000000003L

The function nextprime gives the smallest prime larger than its argument. (Note that the smallest 12-digit number is 1011, not 1012. Great opportunity for an off-by-one mistake.)

Optionally you can provide an addition argument to nextprime to get primes further down the list. For example, this gives the second prime larger than 1011.

    >>> nextprime(10**11, 2)
    100000000019L

What if you wanted the largest 12-digit prime rather than the smallest?

    >>> from sympy import prevprime
    >>> prevprime(10**12)
    999999999989L

Finally, suppose you want to know how many 12-digit primes there are. SymPy has a function primepi that returns the number of primes less than its argument. Unfortunately, it fails for large arguments. It works for arguments as big as 2**27 but throws a memory error for 2**28.

The number of primes less than n is approximately n / log n, so there are about 32 billion primes between 1011 and 1012. According to Wolfram Alpha, the exact number of 12-digit primes is 33,489,857,205. So if you try 12-digit numbers at random, your chances are about 1 in 30 of getting a prime. If you’re clever enough to just pick odd numbers, your chances go up to 1 in 15.