Math

Fitting a parabola to an ellipse and vice versa

Posted on by John

The previous post discussed fitting an ellipse and a parabola to the same data. Both fit well, but the ellipse fit a little better. This will often be the case because an ellipse has one more degree of freedom than a parabola.

There is one way to fit a parabola to an ellipse at an extreme point: match the end points and the curvatures. This uses up all the degrees of freedom in the parabola.

When you take the analogous approach to fitting an ellipse to a parabola, you have one degree of freedom left over. The curvature depends on a ratio, and so you can adjust the parameters while maintaining the ratio. You can use this freedom to fit the parabola better over an interval while still matching the curvature at the vertex.

The rest of the post will illustrate the ideas outlined above.

Fitting a parabola to an ellipse

Suppose you have an ellipse with equation

(x/a)² + (y/b)² = 1.

The curvature at (±a, 0) equals a/b² and the curvature at (0, ±b) equals b/a².

Now if you have a parabola

x = cy² + d

then its curvature at y = 0 is 2|c|.

If you want to match the parabola and the ellipse at (a, 0) then d = a.

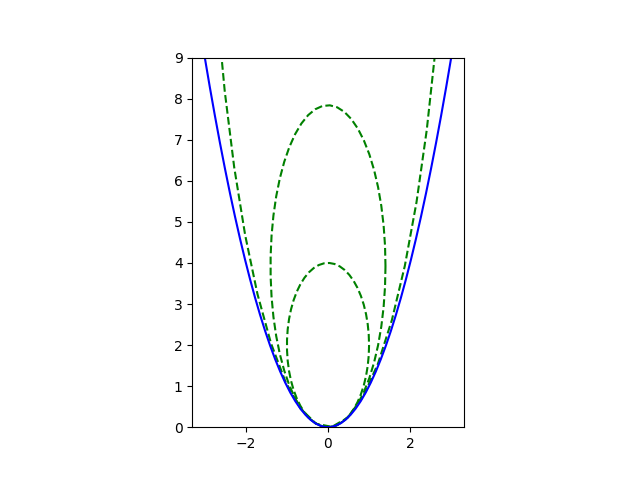
To match the curvatures at (a, 0) we set a/b² = 2|c|. So c = −a/2b². (Without the negative sign the curvatures would match, but the parabola would turn away from the ellipse.)

Similarly, at (−a, 0) we have d = −a and c = a/2b². And at (0,  ±b) we have d = ±b and c = ∓b/2a².

Here’s an example with a golden ellipse.

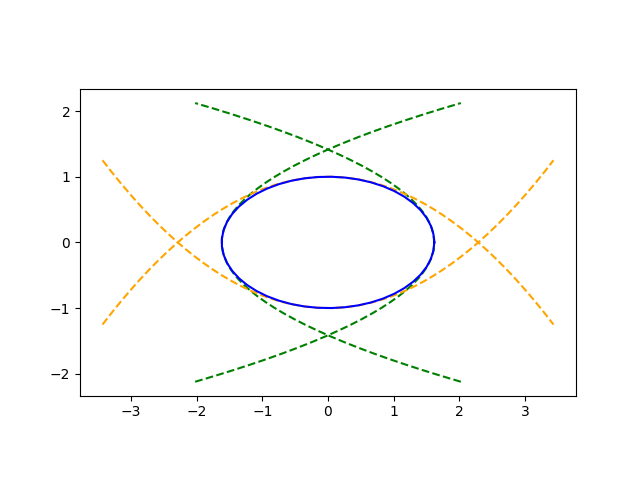
Fitting an ellipse to a parabola

Now we fix the parabola, say

y = cx²

and find an ellipse

(x/a)² + ((y − y0)/b)² = 1

to fit at the vertex (0, 0). For the ellipse to touch the parabola at its vertex we must have

((0 − y0)/b)² = 1

and so y0 = b. To match curvature we have

b/2a² = c.

So a and b are not uniquely determined, only the ratio b/a². As long as this ratio stays fixed at 2c, every ellipse will touch at the vertex and match curvature there. But larger values of the parameters will match the parabola more closely over a wider range. In the limit as b → ∞  (keeping b/a²  = 2c), the ellipses become a parabola.

Related posts

Trinomial Coefficients and Kings

Posted on by John

The term trinomial coefficient is used a couple different ways. The most natural use of the term is a generalization of bionomial coefficients to three variables, i.e. numbers of the form

\frac{n!}{i! \, j! \, k!}

where i + j + k = n. These numbers are the coefficients of yj zk in the expansion of (x + y + z)n.

But there’s another use of the term trinomial coefficient, the one that we are interest in for this post, and that is the coefficients of xk in the expansion of (1 + x + 1/x)n. These numbers can be visualized in a triangle analogous to Pascal’s triangle.

In Pascal’s triangle, each entry is the sum of the two entries above it. In the trinomial triangle, each entry is the sum of the three entries above it.

If you’ve been reading this blog regularly you know I’ve been interested in chess puzzles lately. The thing that make me interested in trinomial coefficients is that they relate to moves of a king on a chessboard.

If you note the number paths a king can take to a square using the minimal number of moves, you get the trinomial triangle. The reason is simple: the number of ways to get to a square equals the number of ways to get there via the square up and to the left, plus the number of ways to get their via the square above, plus the number of ways to get their via the square up and to the right.

Related posts

Hand calculating exp(x)

Posted on by John

The previous post mentioned that Martin Gardner announced that Ramanujan’s conjecture that exp(π√163) in an integer had been proven. This was an April Fool’s joke in 1975. Gardner said

Working by hand, he [Ramanujan] found the value to be 262537412640768743.999999999999… The calculations were tedious, and he was unable to verify the next decimal digits.

Calculating exp(π√163) without a computer—Ramanujan died in 1920—would indeed be tedious, but not insurmountable. Certainly it would not stop someone like Ramanujan from testing a conjecture.

How might you go about calculating exp(π√163) by hand?

Algorithm

One possibility is an algorithm in [1].

\exp(t) = \left(1 + r + \frac{r^2}{2!} + \frac{r^3}{3!} + \cdots \right)^{256} 2^n

where r = t′ / 256, t′ = t − n log 2, and n is chosen to minimize |t′|.

We can choose n so that |t′| < log(2)/2 and so |r| < 0.014. This means the infinite series converges rapidly and not too many terms will be needed, depending on the desired precision.

The calculation x256 can be done by squaring 8 times.

Although the context of this post is hand calculations, this would also be a viable algorithm for a program doing extended precision calculations.

Example

In our case, t = π√163 = 40.1091… and we choose n = 58 so that t′ = −0.09336….

Then r = −0.000364….

So each term in the series will contribute 3 or 4 decimal places to the desired precision at first, more once the factorial denominators get large.

Related posts

[1] Jonathan Borwein and David Bailey. Mathematics by Experiment. Volume 1.

Max and min orbital speed

Posted on by John

An earlier post needed to calculate how much the speed of a planet varies in orbit. The planet moves fastest as perihelion, the point in its orbit closes to the sun, and it moves slowest at aphelion, when it is furthest from the sun.

The ratio of the maximum to minimum speed turns out to be a simple expression in terms of the eccentricity e of the orbit:

(1 + e)/(1 − e).

You can derive this fairly quickly from the vis-viva equation, which in turn is derived from conservation of energy.

There are several things I find interesting about this. First, that the expression is so simple. Second, it can be simplified even more for small e:

(1 + e)/(1 − e) ≈ 1 + 2e.

This comes from expanding the ratio as a series:

(1 + e)/(1 − e) = 1 + 2e + 2e² + 2e³ …

This explains two things from the previous post. First, that the variation in orbital speed, for both Earth and Mars, worked out to be about 2e. The eccentricity of Earth’s orbit is 0.0167 and orbital speed varies by about 3%. Mars’ orbit has eccentricity 0.0934 and its orbital speed varies by about 19%. Since the eccentricity of Mars orbit, while fairly small, is larger than that of Earth, the quadratic term matters more for Mars.

Finally, “I keep running into the function f(z) = (1 − z)/(1 + z),” as I first wrote four years ago, and wrote on again a few months ago. It comes up, for example, in computing impedance, in mental calculation tricks, and in efficient calculation of the perimeter of an ellipse. Now you can add to that list calculating the variation in orbital speed in a two body problem.

Golden convergence

Posted on by John

The golden ratio φ satisfies the following equation.

\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}}

The proof most commonly given is to let x equal the right-hand side of the equation, then observe that x² = 1 + x, the quadratic equation for the golden ratio. The quadratic has two roots: φ and −1/φ. Since x > 1, x = φ.

This proof tacitly assumes that the expression above is meaningfully defined, and then manipulates it algebraically. But is it meaningfully defined? What exactly does the infinitely nested sequence of radicals mean?

You could interpret the nested radicals to be the limit of the iteration

x \mapsto \sqrt{1 + x}

and show that the limit exists.

What should the starting value of our iteration be? It seems natural to choose x = 1, but other values will do. More on that shortly. We could compute φ by implementing the iteration in Python as follows.

    x_old, x_new = 0, 1
    while (abs(x_old - x_new) > 1e-15):
        x_new, x_old = (1 + x_new)**0.5, x_new
    print(x_new)

The program terminates, so the iteration must converge, right? Probably so, but that’s not a proof. To be more rigorous, define

f(x) = \sqrt{1 + x}

and so

f^\prime(x) = \frac{1}{2\sqrt{1 + x}}

This shows 0 < f ′(x) < ½ for any positive x and so the function f(x) is a contraction mapping. This means the iterations converge. We could start with any x > −¾ and the derivative would still be less than 1, so the iterations would converge.

We can visualize the process of convergence starting with x = 0 using the following cobweb plot.

Related posts

Tricks for radix conversion by hand

Posted on by John

The simplest trick for converting from one base to another is grouping. To convert between base b and base bk, group numbers in sets of k and convert one group at a time. To convert from binary to octal, for instance, group bits in sets of three, starting from the right end, and convert each group to octal.

11110010two → (11)(110)(010) → 362eight

For an example going the other direction, let’s convert 476 in base nine to base three.

476nine → (11)(21)(20) → 112120three

In general, conversion between bases is too tedious to do by hand, but one important case where it’s a little easier than it could be is converting between decimal and octal. In combination with the grouping trick above, this means you could, for example, convert between decimal and binary by first converting decimal to octal. Then the conversion from octal to binary is trivial.

The key to converting between decimal and octal is to exploit the fact that 10 = 8 + 2, so powers of 10 become powers of (8 + 2), or powers of 8 become powers of (10 − 2). These tricks are easier to carry out than to explain. You can find descriptions and examples in Knuth’s TAOCP, volume 2, section 4.4.

Knuth cites a note by Walter Soden from 1953 as the first description of the trick for converting octal to decimal.

The trick for moving between base 9 and base 10 (or by grouping, between base 3 and base 10) is simpler and left as an exercise by Knuth. (Problem 12 in section 4.4, with a solution given at the back of the volume.)

Related posts

Double rounding

Posted on by John

The previous post started by saying that rounding has a surprising amount of detail. An example of this is double rounding: if you round a number twice, you might not get the same result as if you rounded directly to the final precision.

For example, let’s say we’ll round numbers ending in 0, 1, 2, 3, or 4 down, and numbers ending in 5, 6, 7, 8, or 9 up. Then if we have a number like 123.45 and round it to one decimal place we have 123.5, and if we round that to an integer we have 124. But if we had rounded 123.45 directly to an integer we would have gotten 123. This is not a mere curiosity; it comes up fairly often and has been an issue in lawsuits.

The double rounding problem cannot happen in odd bases. So, for example, if you have some fraction represented in base 7 and you round it first from three figures past the radix point to two, then from two to one, you’ll get the same result as if you directly rounded from three figures to one. Say we start with 4231.243seven. If we round it to two places we get 4231.24seven, and if we round again to one place we get 4231.3seven, the same result we would get by rounding directly from three places to one.

The reason this works is that you cannot represent ½ by a finite expression in an odd base.

A magical land where rounding equals truncation

Posted on by John

Rounding numbers has a surprising amount of detail. It may seem trivial but, as with most things, there is a lot more to consider than is immediately obvious. I expect there have been hundreds if not thousands of pages devoted to rounding in IEEE journals.

An example of the complexity of rounding is what William Kahan called The Tablemaker’s Dilemma: there is no way in general to know in advance how accurately you’ll need to compute a number in order to round it correctly.

Rounding can be subtle in any number system, but there is an alternative number system in which it is a little simpler than in base 10. It’s base 3, but with a twist. Instead of using 0, 1, and 2 as “digits”, we use −1, 0, and 1. This is known as the balanced ternary system: ternary because of base 3, and balanced because the digits are symmetrical about 0.

We need a symbol for −1. A common and convenient choice is to use T. Think of moving the minus sign from in front of a 1 to on top of it. Now we could denote the number of hours in a day as 10T0 because

1 \times 3^3 + 0 \times 3^2 + (-1)\times 3 + 0 = 24

A more formal way of a describing balanced ternary representation of a number x is a set of coefficients tk such that

x = \sum_{k=-\infty}^\infty t_k 3^k

with the restriction that each tk is in the set {−1, 0, 1}.

Balanced ternary representation has many interesting properties. For example, positive and negative numbers can all be represented without a minus sign. See, for example, Brain Hayes’ excellent article Third Base. The property we’re interested in here is that to round a balanced ternary number to the nearest integer, you simply lop off the fractional part. Rounding is the same as truncation. To see this, note that the largest possible fractional part is a sequence of all 1s, which represents ½:

\frac{1}{3} + \frac{1}{3^2} + \frac{1}{3^3} + \cdots = \frac{1}{2}

Similarly, the most negative possible fractional part is a sequence of all Ts, which represents −½. So unless the fractional part is exactly equal to ½, truncating the fractional part rounds to the nearest integer. If the fractional part is exactly ½ then there is no nearest integer but two integers that are equally near.

Related posts

Falling power analog of binomial theorem

Posted on by John

Yesterday I wrote about how the right notation could make Newton’s interpolation theorem much easier to remember, revealing it as an analog of Taylor series. This post will do something similar for the binomial theorem.

Let’s start with the following identity.

(x + y)(x + y - 1)(x + y - 2) =

x(x - 1)(x - 2) + 3x(x - 1)y + 3xy(y - 1) + y(y - 1)(y - 2)

It’s not clear that this is true, or how one might generalize it. But if we rewrite the equation using falling power notation we have

(x + y)^{\underline{3}} = x^{\underline{3}} + 3x^{\underline{2}} y^{\underline{1}} + 3x^{\underline{1}}y^{\underline{2}} + y^{\underline{3}}

which looks a lot like the binomial theorem. In fact it is the case n = 3 of the Chu-Vandermonde theorem which says

(x + y)^{\underline{n}} = \sum_{k=0}^n \binom{n}{k} x^{\underline{n-k}} y^{\underline{k}}

Viewed purely visually, this is the binomial theorem with little lines under each exponent.

Incidentally, the analogous theorem holds for rising powers. Just change all the lines under the exponents to lines on top of the exponents.

Cycle of New Year’s Days

Posted on by John

Here’s a visualization of how the day of the week for New Year’s Day changes.

The green diamonds represent leap years and the blue squares represent ordinary years.

The day of the week for New Year’s Day advances one day after each ordinary year and two days after each leap year, hence the diagonal stripes in the graph above.

The whole cycle repeats every 28 years. During that 28 year cycle, New Year’s Day falls on each day of the week four times: three times in an ordinary year and once in a leap year. Or to put it another way, each horizontal row of the graph above contains three blue squares and one green diamond.

The comments above are true under the Julian calendar, without exception. And they’re true for long stretches of time under the Gregorian calendar. For example, the pattern above repeats from 1901 to 2099.

The Julian calendar had a leap day every four years, period. This made the calendar year longer than the solar year by about 3 days every 400 years, so the Gregorian calendar removed 3 leap days. A year divisible by 100 is not a leap year unless it is also divisible by 400. So the Gregorian calendar disrupts the pattern above every 100 years.

Related posts