Square root of a small number

Posted on by John

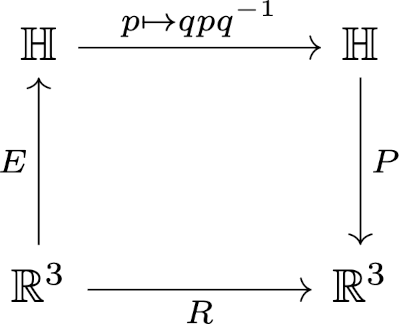
The recent post Converting between quaternions and rotation matrices describes an algorithm as “a mathematically correct but numerically suboptimal method/”

Let’s just look at a small piece of that post. The post explains how to find a rotation matrix to describe the same rotation as pre- and post- multiplying by a unit quaternion q, and how to recover q from a rotation. The latter involves

q0 = ½ √(1 + r11 + r22 + r33).

If you look at the definition of the r terms you’ll see that the quantity under the square root equal 4q0² and so the term is positive. In theory. In floating point arithmetic, the term you’re taking the square root of could be small or even slightly negative.

I mentioned at the bottom of the earlier post that I came up with a unit quaternion q that caused the code to throw an exception because it attempted to take the square root of a negative number.

There’s an easy way to keep the code from throwing an exception: check whether the argument is positive before taking the square root. If it’s positive, forge ahead. If it’s negative, then round it up to zero.

This makes sense. The argument is theoretically positive, so rounding it up to zero can’t do any harm, and in fact it would to a tiny bit of good. But this is missing something.

As a general rule of thumb, if an algorithm has trouble when a quantity is negative, it might have trouble when the quantity is small but positive too.

How could the term

1 + r11 + r22 + r33

which is theoretically positive be computed as a negative number? When all precision is lost in the sum. And this happens when

r11 + r22 + r33

is nearly −1, i.e. when you’re subtracting nearly equal numbers. In general, if two positive numbers a and b are the same up to n bits, you can lose n bits of precision when subtracting them. You could lose all of your precision if two numbers agree to n bits and all you have are n bits.

Putting in a “breaker” to prevent taking the square root of a negative number doesn’t address the problem of code not throwing an exception but returning an inaccurate result. Maybe you’re subtracting two numbers that don’t agree to all the bits of precision you have, but they agree to more bits than you’d care to lose.

The solution to this problem is to come up with another expression for q0 and the components, another expression that is equal in theory but numerically less sensitive, i.e. one that avoids subtracting nearly equal numbers. That’s what the authors do in the paper cited in the previous post.

Why do LLMs have emergent properties?

Posted on by Wayne Joubert

Large language models display emergence behaviors: when the parameter count is scaled to a certain value, suddenly the LLM is capable of performing a new task not possible at a smaller size. Some say the abruptness of this change is merely a spurious artifact of how it is measured. Even so, many would like to understand, predict, and even facilitate the emergence of these capabilities.

The following is not a mathematical proof , but a plausibility argument as to why such behavior should not be surprising, and a possible mechanism. I’ll start with simple cases and work up to more complex ones.

In nature

An obvious point. Emergence is ubiquitous in nature. Ice near the freezing point that is slightly heated suddenly becomes drinkable (phase change). An undrivable car with three wheels gets a fourth wheel and is suddenly drivable. Nonlinearity exists in nature.

In machine learning

A simple example: consider fitting N arbitrary points in one dimension with linear regression using monomials. For a basis up to degree less than N-1, for most possible sets of data points (excluding “special” cases like collinear), the regression error will be non-zero, and reciprocally, the accuracy will be some finite value. Increase the number of monomials (parameter count) to N-1, and suddenly the error drops to zero, and accuracy jumps to infinity.

When using k-means clustering, if one has n clusters and runs k-means clustering with K<N cluster centers, the error will be significant, but when K=N, suddenly the cluster centers can model all clusters well, and the error drops dramatically.

In algorithms

Consider all Boolean circuits composed from some fixed logically complete set of gate types. Now consider the goal of constructing a Boolean circuit that takes a single byte representing the integer N and increments it to N+1, modulo 256 (8 bits input, 8 bits output). Clearly, such a circuit exists, for example, the standard chain of 1-bit add-and-carry circuits. Note one can in principle enumerate all possible circuits of finite gate count. It is manifest that an integer K>0 exists for which no circuit with less than K gates solves the problem but there exists a circuit with K gates that does. The standard chain of 8 1-bit adders might be such a minimizer, or maybe the optimal circuit is more exotic (for example see here, though this method is not guaranteed to compute a minimizer).

One would thus see this capability potentially emerge as soon as one reaches a gate budget of K gates. Now, one could argue that for a smaller gate budget, a partial result might be possible, for example, incrementing any 7-bit number—so the increase in capability is continuous, not emergent or wholly new. However, if all you care about is correctly incrementing any byte (for example, for manipulating ASCII text), then it’s all or nothing; there’s no partial credit. Even so, the gate budget required for incrementing 8 bits compared to only 7-bit integers is only slightly higher, but this minor increase in gate count actually doubles the quantity of integers that can be incremented, which might be perceived as a surprising, unexpected (emergent) jump.

In LLMs

The parameter count of an LLM defines a certain bit budget. This bit budget must be spread across many, many tasks the final LLM will be capable of, as defined by the architecture and the training process (in particular, the specific mix of training data). These tasks are implemented as “algorithms” (circuits) within the LLM. The algorithms are mixed together and (to some extent) overlap in a complex way that is difficult to analyze.

Suppose one of these desired capabilities is some task X. Suppose all possible input/output pairs for this operation are represented in the training data (or, maybe not—maybe some parts of the algorithm can be interpolated from the training data). The LLM is trained with SGD, typically with 2-norm minimization. The unit ball in the 2-norm is a sphere in high dimensional space. Thus “all directions” of the loss are pressed down equally by the minimization process—which is to say, the LLM is optimized on all the inputs for many, many tasks, not just task X. The limited parameter bit budget must be spread across many, many other tasks the LLM must be trained to do. As LLMs of increasing size are trained, at some point enough parameter bits in the budget will be allocatable to represent a fully accurate algorithm for task X, and at this point the substantially accurate capability to do “task X” will be perceivable—“suddenly.”

Task X could be the 8-bit incrementer, which from an optimal circuit standpoint would manifest emergence, as described above. However, due to the weakness of the SGD training methodology and possibly the architecture, there is evidence that LLM training does not learn optimal arithmetic circuits at all but instead does arithmetic by a “bag of heuristics” (which incidentally really is, itself, an algorithm, albeit a piecemeal one). In this case, gradually adding more and more heuristics might be perceived to increase the number of correct answers in a somewhat more incremental way, to be sure. However, this approach is not scalable—to perform accurate arithmetic for any number of digits, if one does not use an exact arithmetic algorithm or circuit, one must use increasingly more heuristics to increase coverage to try to capture all possible inputs accurately. And still, transitioning from an approximate to an exact 8-bit incrementer might in practice be perceived as an abrupt new capability, albeit a small one for this example.

One could alternatively consider tool use (for example, a calculator function that is external to the LLM proper), but then a new tool must be written for every new task, and the LLM needs to understand how to use the tool. (Maybe at some point LLMs will know how to write and use their own algorithmic tools?)

Predicting emergence

The real question is how can we predict when a new LLM will achieve some new capability X. For example, X = “Write a short story that resonates with the social mood of the present time and is a runaway hit” (and do the same thing again once a year based on new data, indefinitely into the future without failure). We don’t know an “algorithm” for this, and we can’t even begin to guess the required parameter budget or the training data needed. That’s the point of using an LLM—its training internally “discovers” new, never seen before algorithms from data that would be difficult for humans to formulate or express from first principles. Perhaps there is some indirect way of predicting the emergence of such X, but it doesn’t seem obvious on the face of it how to predict this directly.

Conclusion

Based on these examples, it would seem not at all surprising for LLMs to exhibit emergent behaviors, though in our experience our encounter with them may be startling. Predicting them may be possible to a limited extent but for the general case seems really hard.

Do you have any thoughts? If so, please leave them in the comments.

Converting between quaternions and rotation matrices

Posted on by John

In the previous post I wrote about representing rotations with quaternions. This representation has several advantages, such as making it clear how rotations compose. Rotations are often represented as matrices, and so it’s useful to be able to go between the two representations.

A unit-length quaternion (q0, q1, q2, q3) represents a rotation by an angle θ around an axis in the direction of (q1, q2, q3) where cos(θ/2) = q0. The corresponding rotation matrix is given below.

R = \begin{pmatrix} 2(q_0^2 + q_1^2) - 1 & 2(q_1 q_2 - q_0 q_3) & 2(q_1 q_3 + q_0 q_2) \\ 2(q_1 q_2 + q_0 q_3) & 2(q_0^2 + q_2^2) - 1 & 2(q_1 q_3 - q_0 q_1) \\ 2(q_1 q_3 - q_0 q_2) & 2(q_2 q_3 + q_0 q_1) & 2(q_0^2 + q_3^2) - 1 \end{pmatrix}

Going the other way around, inferring a quaternion representation from a rotation matrix, is harder. Here is a mathematically correct but numerically suboptimal method known [1] as the Chiaverini-Siciliano method.

\begin{align*} q_0 &= \frac{1}{2} \sqrt{1 + r_{11} + r_{22} + r_{33}} \\ q_1 &= \frac{1}{2} \sqrt{1 + r_{11} - r_{22} - r_{33}} \text{ sgn}(r_{32} - r_{32}) \\ q_2 &= \frac{1}{2} \sqrt{1 - r_{11} + r_{22} - r_{33}} \text{ sgn}(r_{13} - r_{31}) \\ q_3 &= \frac{1}{2} \sqrt{1 - r_{11} - r_{22} + r_{33}} \text{ sgn}(r_{21} - r_{12}) \end{align*}

Here sgn is the sign function; sgn(x) equals 1 if x is positive and −1 if x is negative. Note that the components only depend on the diagonal of the rotation matrix, aside from the sign terms. Better numerical algorithms make more use of the off-diagonal elements.

Accounting for degrees of freedom

Something seems a little suspicious here. Quaternions contain four real numbers, and 3 by 3 matrices contain nine. How can four numbers determine nine numbers? And going the other way, out of the nine, we essentially choose three that determine the four components of a quaternion.

Quaternions have four degrees of freedom, but we’re using unit quaternions, so there are basically three degrees of freedom. Likewise orthogonal matrices have three degrees of freedom. An axis of rotation is a point on a sphere, so that has two degrees of freedom, and the degree of rotation is the third degree of freedom.

In topological terms, the unit quaternions and the set of 3 by 3 orthogonal matrices are both three dimensional manifolds, and the former is a double cover of the latter. It is a double cover because a unit quaternion q corresponds to the same rotation as −q.

Python code

Implementing the equations above is straightforward.

import numpy as np

def quaternion_to_rotation_matrix(q):
    q0, q1, q2, q3 = q
    return np.array([
        [2*(q0**2 + q1**2) - 1, 2*(q1*q2 - q0*q3), 2*(q1*q3 + q0*q2)],
        [2*(q1*q2 + q0*q3), 2*(q0**2 + q2**2) - 1, 2*(q2*q3 - q0*q1)],
        [2*(q1*q3 - q0*q2), 2*(q2*q3 + q0*q1), 2*(q0**2 + q3**2) - 1]
    ]) 

def rotation_matrix_to_quaternion(R):
    r11, r12, r13 = R[0, 0], R[0, 1], R[0, 2]
    r21, r22, r23 = R[1, 0], R[1, 1], R[1, 2]
    r31, r32, r33 = R[2, 0], R[2, 1], R[2, 2]
    
    # Calculate quaternion components
    q0 = 0.5 * np.sqrt(1 + r11 + r22 + r33)
    q1 = 0.5 * np.sqrt(1 + r11 - r22 - r33) * np.sign(r32 - r23)
    q2 = 0.5 * np.sqrt(1 - r11 + r22 - r33) * np.sign(r13 - r31)
    q3 = 0.5 * np.sqrt(1 - r11 - r22 + r33) * np.sign(r21 - r12)
    
    return np.array([q0, q1, q2, q3])

Random testing

We’d like to test the code above by generating random quaternions, converting the quaternions to rotation matrices, then back to quaternions to verify that the round trip puts us back essentially where we started. Then we’d like to go the other way around, starting with randomly generated rotation matrices.

To generate a random unit quaternion, we generate a vector of four independent normal random values, then normalize by dividing by its length. (See this recent post.)

To generate a random rotation matrix, we use a generator that is part of SciPy.

Here’s the test code:

def randomq():
    q = norm.rvs(size=4)
    return q/np.linalg.norm(q)

def randomR():
    return special_ortho_group.rvs(dim=3)

np.random.seed(20250507)
N = 10

for _ in range(N):
    q = randomq()
    R = quaternion_to_rotation_matrix(q)
    t = rotation_matrix_to_quaternion(R)
    print(np.linalg.norm(q - t))
    
for _ in range(N):
    R = randomR()
    q = rotation_matrix_to_quaternion(R)
    T = quaternion_to_rotation_matrix(q)
    print(np.linalg.norm(R - T))

The first test utterly fails, returning six 2s, i.e. the round trip vector is as far as possible from the vector we started with. How could that happen? It must be returning the negative of the original vector. Now go back to the discussion above about double covers: q and −q correspond to the same rotation.

If we go back and add the line

    q *= np.sign(q[0])

then we standardize our random vectors to have a positive first component, just like the vectors returned by rotation_matrix_to_quaternion.

Now our tests all return norms on the order of 10−16 to 10−14. There’s a little room to improve the accuracy, but the results are good.

Update: I did some more random testing, and found errors on the order of 10−10. Then I was able to create a test case where rotation_matrix_to_quaternion threw an exception because one of the square roots had a negative argument. In [1] the authors get around this problem by evaluating two theoretically equivalent expressions for each of the square root arguments. The expressions are complementary in the sense that both should not lead to numerical difficulties at the same time.

[1] See “Accurate Computation of Quaternions from Rotation Matrices” by Soheil Sarabandi and Federico Thomas for a better numerical algorithm. See also the article “A Survey on the Computation of Quaternions From Rotation Matrices” by the same authors.

Composing rotations using quaternions

Posted on by John

Every rotation in 3D fixes an axis [1]. This is Euler’s rotation theorem from 1775. Another way to state the theorem is that no matter how you rotate a sphere about its center, two points stay fixed.

The composition of two rotations is a rotation. So the first rotation fixes some axis, the second rotation fixes some other axis, and the composition fixes some third axis. It’s easy to see what these axes are if we work with quaternions. (Quaternions were discovered decades after Euler proved his rotation theorem.)

A rotation by θ about the axis given by a unit vector v = (v1, v2, v3) corresponds to the quaternion

q = (cos(θ/2), sin(θ/2)v1, sin(θ/2)v2, sin(θ/2)v3).

To rotate a point p = (p1, p2, p3) by an angle θ about the axis v, first embed p as a quaternion by setting its first coordinate to 0:

p → (0, p1, p2, p3)

and multiply the quaternion p on the left by q and on the right by the conjugate of q, written q*. That is, the rotation takes p to

p′ = qpq*.

This gives us a quaternion p′, not a 3D vector. We recover the vector by undoing the embedding, i.e. chopping off the first coordinate.

Making things clearer

Since q has unit length, the conjugate of q is also its inverse: q* = q−1. Usually rotations are described as above: multiply on the left by q and on the right by q*. In my opinion it’s clearer to say

p′ = qpq−1.

Presumably sources say q* instead of q−1 because it’s obvious how to compute q* from q; it’s not quite as obvious that this also gives the inverse of q.

Another thing about the presentation above that, while standard, could be made clearer is the role Euclidean space and quaternions. It’s common to speak of the real and quaternion representations of a vector, but we could make this more explicit by framing this as an embedding E from ℝ³ to the quaternions ℍ and a projection P from ℍ back to ℝ³ [3].

\[\begin{tikzcd} {\mathbb{H}} && {\mathbb{H}} \\ \\ {\mathbb{R}^3} && {\mathbb{R}^3} \arrow[

The commutative diagram says we end up with the same result regardless of which of two paths we take: we can do the rotation directly from ℝ³ to ℝ³, or we could project into ℍ, multiply by q on the left and divide by q on the right, and project back down to ℝ³.

Composition

Composing rotations represented by quaternions is simple. Rotating by a quaternions q and then by a quaterion r is the same as rotating by rq. Proof:

r(qpq−1)r−1 = (rq)p(q−1r−1) = (rq)p(rq)−1.

See the next post for how to convert between quaternion and matrix representations of a rotation.

Related posts

[1] Note that this is not the case in two dimensions, nor is it true in higher even dimensions.

[2] We assumed v had unit length as a vector in ℝ³. So

||q||² = cos²(θ/2) + sin²(θ/2) = 1.

[3] Why ℍ for quaternions? ℚ for rationals was already taken, so we use ℍ for William Rowan Hamilton.

5,000th post

Posted on by John

This is the 5,000th post on this blog. I started blogging in 2008, and Wayne Joubert started contributing posts last year. We’ve written an average of between five and six posts a week for the last 17 years.

I thought about listing some of the most popular posts over the years, but that’s not as simple as it sounds. Popularity varies over time, and posts are popular with different people for different reasons. I don’t have a way of quantifying what posts have been popular with regular readers, but I’m sure such a list would be very different from the lists below.

Recent favorites

Here are posts that have been popular over the last year.

I knew that the ASCII post was popular, but before looking at stats I had no idea anyone was reading the other two posts. I imagine regular readers are more interested in things like my recent series on the logistic map.

Hacker News

The first post to go viral was Why programmers are not paid in proportion to their productivity. Hacker News sent the site more traffic than it could handle at the time.

Many of the posts that have seen a lot of traffic have been posted on Hacker News. I very much appreciate everyone who posts my work there. Because Hacker News readers tend to be programmers, my most popular posts have tended to be programming-related. The posts most popular with regular readers are not as tilted toward programming.

Here are a few more posts that have been popular because of Hacker News.

Code snippets

I didn’t realize until Tim Hopper pointed it out that a lot of projects on Github mention this blog, either to cite an article as a reference or to use code I’ve posted. That’s fine, by the way: feel free to use whatever you find useful. Here is Tim’s list of mentions.

Here’s an index of stand-alone code. Everything these code snippets do can be found in standard software libraries. However, these code samples remain popular because sometimes you cannot import a library or do not want to. I mentioned an example of this in the previous post. I’ve had several consulting projects where there was something new about their project that meant they had to develop basic mathematical software from scratch.

Calculators

This site started as a set of hand-written HTML pages, and there are a still a few such pages, especially calculators. Some of these have been surprisingly popular. (“Surprising” and “popular” seem to always go together. I can kinda predict when something will be moderately popular, but the most popular content is always a surprise to me.)

A note to new readers

If you’re new to this site, the links above may give a wrong impression. I mostly write about math and statistics, and occasionally about other topics such as data privacy or music. None of the posts above are typical.

If you’d like to be notified of posts as they come out, you can subscribe via RSS or follow one of my X accounts. I also have a newsletter where I introduce posts two or three at a time.

Thanks for reading.

A simple way to generate random points on a sphere

Posted on by John

I recently ran across a simple way to generate random points uniformly distributed on a sphere: Generate random points in a cube until you get one inside the sphere, then push it to the surface of the sphere by normalizing it [1].

In more detail, to generate random points on the unit sphere, generate triples

(u1, u2, u3)

of independent random values uniformly generated on [−1, 1] and compute the sum of there squares

S² = u1² + u2² + u3²

If S² > 1 then reject the sample and try again. Otherwise return

(u1/S, u2/S, u3/S).

There are a couple things I like about this approach. First, it’s intuitively plausible that it works. Second, it has minimal dependencies. You could code it up quickly in a new environment, say in an embedded system, though you do need a square root function.

Comparison with other methods

It’s not the most common approach. The most common approach to generate points on a sphere in n dimensions is to generate n independent values from a standard normal distribution, then normalize. The advantage of this approach is that it generalizes efficiently to any number of dimensions.

It’s not obvious that the common approach works, unless you’ve studied a far amount of probability, and it raises the question of how to generate samples from normal random variable. The usual method, the Box-Muller algorithm, requires a logarithm and a sine in addition to a square root.

The method starting with points in a cube is more efficient (when n = 3, though not for large n) than the standard approach. About half the samples that you generate from the cube will be thrown out, so on average you’ll need to generate six values from [−1, 1] to generate one point on the sphere. It’s not the most efficient approach—Marsaglia gives a faster algorithm in the paper cited aove—but it’s good enough.

Accept-reject methods

One disadvantage to accept-reject methods in general is that although they often have good average efficiency, their worst-case efficiency is theoretically infinitely bad: it’s conceivable that you’ll reject every sample, never getting one inside the sphere. This is not a problem in practice. However, it may be a problem in practice that the runtime is variable.

When computing in parallel, a task may have to wait on the last thread to finish. The runtime for the task is the runtime of the slowest thread. In that case you may want to use an algorithm that is less efficient on average but that has constant runtime.

It also matters in cryptography whether processes have a constant runtime. An attacker may be able to infer something about the path taken through code by observing how long it took for the code to execute.

Related posts

[1] George Marsaglia. Choosing a point from the surface of a sphere. The Annals of Mathematical Statistics. 1972, Vol. 43, No. 2, 645–646.

Recamán’s sequence

Posted on by John

I recently ran into Recamán’s sequence. N. J. A. Sloane, the founder of the Online Encyclopedia of Integer Sequences calls Recamán’s sequence one of his favorites. It’s sequence A005132 in the OEIS.

This sequence starts at 0 and the nth number in the sequence is the result of moving forward or backward n steps from the previous number. You are allowed to move backward if the result is positive and a number you haven’t already visited. Otherwise you move forward.

Here’s Python code to generate the first N elements of the sequence.

    def recaman(N):
        a = [0]*N
        for n in range(1, N):
            proposal = a[n-1] - n
            if proposal > 0 and proposal not in set(a):
                a[n] = proposal
            else:
                a[n] = a[n-1] + n
        return a

For example, recaman(10) returns

    [0, 1, 3, 6, 2, 7, 13, 20, 12, 21]

There’s a Numberphile video that does two interesting things with the sequence: it visualizes the sequence and plays a representation of the sequence as music.

The rules for the visualization are that you connect consecutive elements of the sequence with circular arcs, alternating arcs above and below the numberline.

Here’s code to reproduce an image from the video.

    import numpy as np
    import matplotlib.pyplot as plt
    
    def draw_arc(a, b, n):
        c = (a + b)/2
        r = max(a, b) - c
        t = np.linspace(0, np.pi) * (-1)**(n+1)
        plt.plot(c + r*np.cos(t), r*np.sin(t), 'b')
           
    N = 62
    a = recaman(N)
    for n in range(N-1):
        draw_arc(a[n], a[n+1], n)
    plt.gca().set_aspect("equal")
    plt.show()

Here’s the output:

To create a music sequence, associate the number n with the nth note of the chromatic scale. You can listen to the music in the video; here’s sheet music made with Lilypond.

Update

Here is another Recamán visualization going further out in the sequence. I made a few aesthetic changes at the same time.

I’ve also made higher resolution versions of the images in this post. Here are SVG and PDF versions of the first visualization.

Here is a PDF of the sheet music.

And here are SVG and PDF versions of the new visualization.

Cycle order in period doubling region

Posted on by John

The last four post have looked at the bifurcation diagram for the logistic map.

There was one post on the leftmost region, where there is no branching. Then two posts on the region in the middle where there is period doubling. Then a post about the chaotic region in the end.

This post returns the middle region. Here’s an image zooming in on the first three forks.

The nth region in the period doubling region has period 2n.

I believe, based on empirical results, that in each branching region, the branches are visited in the same order. For example, in the region containing r = 3.5 there are four branches. If we number these from bottom to top, starting with for the lowest branch, I believe a point on branch 0 will go to a point on branch 2, then branch 1, then branch 3. In summary, the cycle order is [0, 2, 1, 3].

Here are the cycle orders for the next three regions.

[0, 4, 6, 2, 1, 5, 3, 7]

[0, 8, 12, 4, 6, 14, 10, 2, 1, 9, 13, 5, 3, 11, 7, 15]

[0, 16, 24, 8, 12, 28, 20, 4, 6, 22, 30, 14, 10, 26, 18, 2, 1, 17, 25, 9, 13, 29, 21, 5, 3, 19, 27, 11, 7, 23, 15, 31]

[0, 32, 48, 16, 24, 56, 40, 8, 12, 44, 60, 28, 20, 52, 36, 4, 6, 38, 54, 22, 30, 62, 46, 14, 10, 42, 58, 26, 18, 50, 34, 2, 1, 33, 49, 17, 25, 57, 41, 9, 13, 45, 61, 29, 21, 53, 37, 5, 3, 35, 51, 19, 27, 59, 43, 11, 7, 39, 55, 23, 15, 47, 31, 63]

Two questions:

  1. Is the cycle order constant within a region of a constant period?
  2. If so, what can be said about the order in general?

I did a little searching into these questions, and one source said there are no known results along these lines. That may or may not be true, but it suggests these are not common questions.

An island of stability in a sea of chaos

Posted on by John

The last several posts have been looking at the bifurcation diagram below in slices.

logistic bifurcation diagram

The first post looked at the simple part, corresponding to the horizontal axis r running from 0 to 3.

The next post looked at the first fork, for r between 3 and 3.4495.

The previous post looked at the period doubling region, for r between 3.4495 and 3.56995.

For r greater than about 3.56995 we enter the chaotic region. This post looks at an apparent island of stability inside the chaotic region. This island starts at r = 1 + √8 = 3.8284.

The whitespace indicates an absence of stable cycle points. There are unstable cycle points, infinitely many in fact, as we will soon see. For a small range of r there are three stable cycle points. When r = 3.83, for example, the three cycle points are 0.1561, 0.5047, and 0.9574.

This is significant because period three implies chaos. There is a remarkable theorem that says if a continuous map of a bounded interval to itself has a point with period 3, then it also has points with periods 4, 5, 6, … as well as an uncountable number of points with no period. If there are points with period 4, why can’t we see them? Because they’re unstable. You would have to land exactly on one of these points to go in a cycle. If you’re off by the tiniest amount, which you always are in computer arithmetic, you won’t stay in the cycle.

So even when we’re in the region with three stable points, things are still technically chaotic.

There seems to be something paradoxical about computer demonstrations of chaos. If you have extremely sensitive dependence on initial conditions, how can floating point operations, which are not exact, demonstrate chaos? I would say they can illustrate chaos rather than demonstrate chaos. And sometimes you can do computer calculations which do not have such sensitivity to show that other things are sensitive.

For example, I asserted above that there are points with period 4. Let f be the logistic map with r = 3.83

f(x) = 3.83 x(1 − x)

and define

p(x) = f(f(f(f(x)))),

i.e. four applications of f. Then you can see that there must be a point with period 4 because the graph of p(x) crosses the graph of x.

So while our region of whitespace appears to be empty except for three stable cycle points, there are infinitely many more cyclic points scattered like invisible dust in the region, a set of measure zero that we cannot see.

Spacing between branches

Posted on by John

The last couple posts have been looking at the logistic bifurcation diagram a little at a time.

logistic bifurcation diagram

The first post in the series looked at the details of that part of the diagram that looks like the graph of a function, where there parameter r in the logistic map

f(x) = r x(1 − x)

varies from o to 3.

The first branch point occurs at r = 3. When r is exactly equal to 3, almost all starting points converge to the same point, though they converge very slowly. When r is slightly larger than 3 the (stable) iterates no longer converge to a point but instead oscillate between two points.

The second post in this series looked at the first fork, corresponding to values of r from 3 to 1 + √6. For r larger than 1 + √6 the previous stable cycle points become unstable and split into two new cycles each. These new cycles will split (“bifurcate”) into two new cycles, and so on and so on until there are infinitely many cycles and chaos breaks out around r = 3.56995.

This post will look at the horizontal spacing between branch points.

The first branch point occurs when r equals b1 = 3.

The two branches branch again when r crosses b2 = 1 + √6.

The next branch point is b3 = 3.5440903…. Why is there a simple expression for b1 and b2 but not for b3? Everything gets more complicated as r increases. The number b3 is algebraic, the root of a 12th degree polynomial [1].

t12 − 12t11 + 48t10 − 40t9 − 193t8 + 392t7 + 44t6 + 8t5 − 977t4 − 604t3 + 2108t2 + 4913 = 0

The number b4 has algebraic also been shown to be algebraic: someone found a 120-degree polynomial with integer coefficients such that −b4(b4 − 2) is a root [1]. The coefficients in the polynomial vary over 72 orders of magnitude. Perhaps its possible to find polynomials with other branch points as roots, but this doesn’t seem promising or practical.

The spacing between branch points decreases rapidly, becoming infinitely small before chaos breaks out. The ratio of spacings between consecutive branch points converges to a constant, known as Feigenbaum’s constant

δ = 4.66920…

This constant is known to surprising precision. Directly computing the constant to high precision by numerically finding branch points would be impractical, but Feigenbaum came up with an indirect way of computing his constant via a functional equation. The constant δ has been computed at least 1018 digits.

Feigenbaum’s constant does not just apply to the iterations of the logistic map. It’s a “universal” constant in that it applies to a class of dynamical systems.

Previous posts in this series

[1] Jonathan Borwein and David Bailey. Mathematics by Experiment: Plausible Reasoning in the 21st Century. 2004.