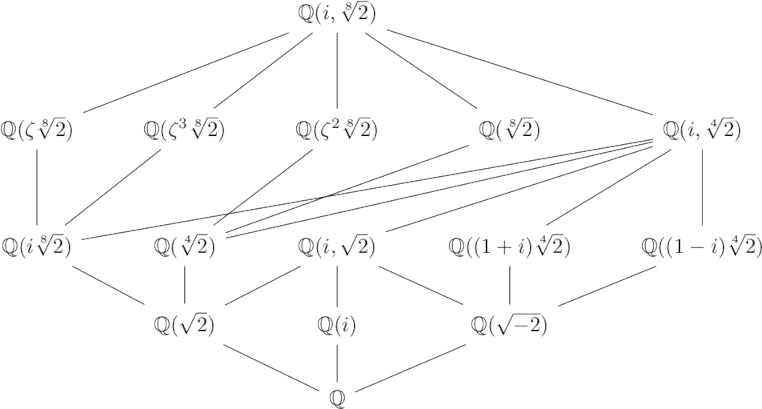
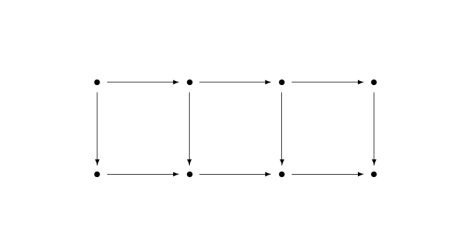
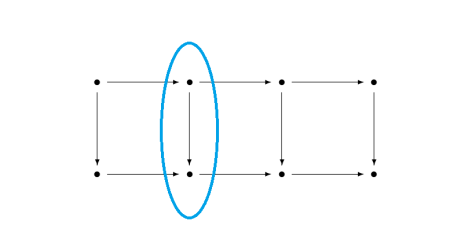
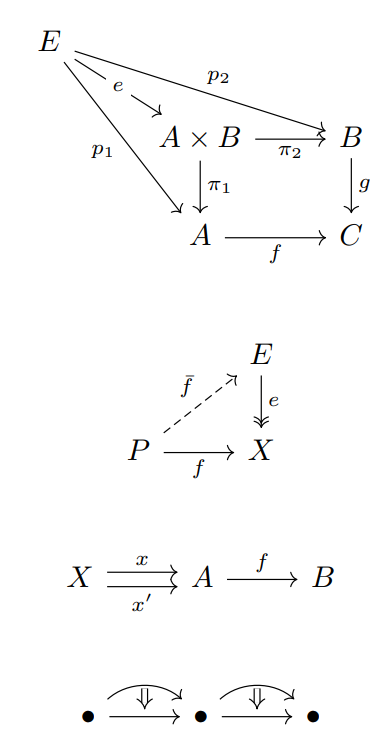I was bewildered by my first exposure to category theory. My first semester in graduate school I had a textbook with definitions like “A gadget is an object G such that whenever you have this unfamiliar constellation of dots and arrows, you’re allowed to draw another arrow from here to there.” What? Why?!
I revisited category theory occasionally after college, going through cycles of curiosity followed by revulsion. It took several cycles before I could put my finger on why I found category theory so foreign.
There are numerous obstacles to appreciating category theory, but the biggest may be diagrammatic reasoning. More specifically, having to learn diagrammatic reasoning at the same time as facing other challenges.
Why should diagrammatic reasoning be difficult? Isn’t the purpose of diagrams to make things clearer?
Usually diagrams are supplementary. They illustrate things that are described verbally. But in category theory, the diagrams are primary, not supplementary. Instead, you have definitions and theorems stated in the language of diagrams [1].
In practice, category theory uses a style of presentation you’re unlikely to have seen anywhere else. But this is not essential. You could do category theory without drawing diagrams, though nobody does. And, importantly for this post, you can use category theory-like diagrams without reference to categories. That’s what William Lawvere does in his book Conceptual Mathematics. The book uses Karate Kid-like pedagogy: the student gains fluency with a practice before being told its significance.
When you see a triangle made of two arrows, what’s the significance of the existence of an arrow that makes the diagram into a triangle? What difference does it make when the missing arrow goes on one side of the diagram or the other as in the two diagrams below?

The answer is not obvious if you’re unfamiliar with this way of thinking, and yet the problem has nothing to do with category theory per se. You could ask the question in the context of finite sets and functions. And that’s what Lawvere’s book does, acquainting the reader with diagrammatic reasoning before getting into category theory as such.
***
[1] Or more to the heart of the matter, you have definitions in terms of functions (“morphisms”) that are represented by diagrams. The difficulty does not come from the diagrams but rather from formulating things in terms of the existence and uniqueness of functions rather than more tangible arguments about sets and elements. This indirect formulation may seem unnecessary, or even sadistic, but it is generalizes further.