Geodesy

Projecting the globe onto regular solids

Posted on by John

I was playing around with some geographic features of Mathematica this morning and ran across an interesting example in the documentation for the PolyhedronProjection function given here. Here’s what you get when you project a map of the earth onto each of the five regular (Platonic) solids.

dodecahedron

icosahedron
octahedron
cube
tetrahedron

How the images were made

At first I right-clicked on each image and saved as graphic files. This produced low quality images, even when I saved as SVG. I got better resolution by using the Export command and specifying the ImageSize and ImageResolution options.

The default view of the tetrahedron was face-on, so it looked like a flat triangle. By changing the ViewPoint I was able to get something that’s more clearly three dimensional.

By the way, you can use PolyhedronProjection to project onto more exotic polyhedra than the Platonic solids. For example,

    Export["rhomb.png", 
        PolyhedronProjection["ParagyrateDiminishedRhombicosidodecahedron"], 
        ImageResolution -> 72, 
        ImageSize -> Large]

produces this:

ParagyrateDiminishedRhombicosidodecahedron

More regular solid posts

Equal Earth map projection

Posted on by John

There’s no perfectly satisfying way to map the globe on to a flat surface. Every projection has its advantages and disadvantages. The Mercator projection, for example, is much maligned for the way it distorts area, but it has the property that lines of constant bearing correspond to straight lines on the map. Obviously this is convenient if you’re sailing without GPS. But for contemporary use, say in a classroom, minimizing area distortion is often a higher priority than keeping bearing lines straight.

Bojan Šavrič, Tom Patterson, and Bernhard Jenny have developed a new map projection called Equal Earth that nicely balances several competing criteria, including aesthetics.

Equal earth projection

The Equal Earth projection satisfies the following mathematical criteria:

  1. Equal area: The area of a region on the globe is proportional to the area of its projection.
  2. Straight parallels: Lines of equal latitude project on to horizontal lines.
  3. Regularly distributed meridians: At a given latitude, the spacing between lines of longitude are equal.
  4. Bilateral symmetry: The projection is symmetric with respect to the x-axis (equator) and y-axis (prime meridian).

Here are the equations for the Equal Earth projection.

\begin{eqnarray*} \sin\theta &=& \frac{\sqrt{3}}{2} \sin \phi \\ x &=& \frac{2\sqrt{3}}{3} \frac{\lambda \cos \theta}{a_1+ 3a_2 \theta^2 + \theta^6(7a_3 + 9a_4\theta^2)} \\ y &=& \theta (a_1 + a_2\theta^2 + \theta^6(a_3 + a_4\theta^2)) \end{eqnarray*}

Here λ and φ are longitude and latitude respectively. The parametric latitude θ is introduced for convenience and is simply a rescaling of latitude φ.

The parameters ai are given below.

    a_1 =  1.340264 
    a_2 = -0.081106 
    a_3 =  0.000893 
    a_4 =  0.003796

You can find more in their paper: Bojan Šavrič, Tom Patterson, and Bernhard Jenny. The Equal Earth map projection. International Journal of Geographical Information Science. https://doi.org/10.1080/13658816.2018.1504949.

More geography posts

Misplacing a continent

Posted on by John

There are many conventions for describing points on a sphere. For example, does latitude zero refer to the North Pole or the equator? Mathematicians tend to prefer the former and geoscientists the latter. There are also varying conventions for longitude.

Volker Michel describes this clash of conventions colorfully in his book on constructive approximation.

Many mathematicians have faced weird jigsaw puzzles with misplaced continents after using a data set from a geoscientist. If you ever get such figures, too, or if you are, for example, desperately searching South America in a data set but cannot find it, remember the remark you have just read to solve your problem.

More geography posts

Ellipsoid surface area

Posted on by John

How much difference does the earth’s equatorial bulge make in its surface area?

To first approximation, the earth is a sphere. The next step in sophistication is to model the earth as an ellipsoid.

The surface area of an ellipsoid with semi-axes a ≥ b ≥ c is

A = 2\pi \left( c^2 + \frac{ab}{\sin\phi} \left( E(\phi, k) \sin^2\phi + F(\phi, k) \cos^2 \phi\right)\right)

where

\cos \phi = \frac{c}{a}

and

m = k^2 = \frac{a^2(b^2 - c^2)}{b^2(a^2 - c^2)}

The functions E and F are incomplete elliptic integrals

F(\phi, k) = \int_0^\phi \frac{d\theta}{\sqrt{1 - k^2 \sin^2\theta}}

and

E(\phi, k) = \int_0^\phi \sqrt{1 - k^2 \sin^2\theta}\,d\theta

implemented in SciPy as ellipeinc and ellipkinc. Note that the SciPy functions take m as their second argument rather its square root k.

For the earth, a = b and so m = 1.

The following Python code computes the ratio of earth’s surface area as an ellipsoid to its area as a sphere.

from numpy import pi, sin, cos, arccos
from scipy.special import ellipkinc, ellipeinc

# values in meters based on GRS 80
# https://en.wikipedia.org/wiki/GRS_80
equatorial_radius = 6378137
polar_radius = 6356752.314140347

a = b = equatorial_radius
c = polar_radius

phi = arccos(c/a)
# in general, m = (a**2 * (b**2 - c**2)) / (b**2 * (a**2 - c**2))
m = 1

temp = ellipeinc(phi, m)*sin(phi)**2 + ellipkinc(phi, m)*cos(phi)**2
ellipsoid_area = 2*pi*(c**2 + a*b*temp/sin(phi))

# sphere with radius equal to average of polar and equatorial
r = 0.5*(a+c)
sphere_area = 4*pi*r**2

print(ellipsoid_area/sphere_area)

This shows that the ellipsoid model leads to 0.112% more surface area relative to a sphere.

Source: See equation 19.33.2 here.

Update: It was suggested in the comments that it would be better to compare the ellipsoid area to that of a sphere of the same volume. So instead of using the average of the polar and equatorial radii, one would take the geometric mean of the polar radius and two copies of the equatorial radius. Using that radius, the ellipsoid has 0.0002% more area than the sphere.

Update 2: This post gives a simple but accurate approximation for the area of an ellipsoid.

A book I’d like (someone) to write

Posted on by John

Here’s an idea I had for a book. Maybe someone has already written it. If you know of such a book, please let me know.

Differential geometry has a huge ratio of definitions to theorems. It seems like you do nothing but study definitions for a semester or two in preparation for proving something later. It’s easy to lose sight of the geometry. I’d like to see a book that is a concrete complement more typical abstract books.

My suggestion is for someone to write a book that goes through a standard differential geometry book, like Spivak’s, and compute everything for a small number of example manifolds: at least a sphere and an ellipsoid, maybe a torus. The book would first go through everything on a sphere where things are simplest, then generalize to an ellipsoid. There would be a lot of applications to geodesy: to first approximation the earth is a sphere, to second approximation it is an ellipsoid.

Sometimes a calculation, such as arc length, is very simple on a sphere. It can be done just using trig. Then the analogous calculation on an ellipsoid is much harder. It is complicated enough to illustrate the machinery of differential geometry. However, we know the answers shouldn’t be much different from those for a sphere, so we have a way to see whether the results are reasonable. This book would not shy away from computational difficulties.

I imagine this book would have lots of illustrations. It might even come with physical models, such as a globe with an exaggerated equatorial bulge. The idea is to be as tangible as other books are abstract.

I don’t plan to write this book, at least not any time soon. Maybe if my consulting goes well I would have the time to work on it in the future, but now is not the time for me to write a book. In the mean time, if someone wants to scoop my idea, please do!

* * *

Here are a couple other book ideas I’ve blogged about: R: The Good Parts and a rigorous elementary statistics text.

And here are some posts on geodesy: What is the shape of the earth? and Latitude doesn’t exactly mean what I thought.

And finally a few posts on spherical geometry: Napier’s mnemonic, The Sydney Opera House, and Mercator projection.

Spotting sensitivity in an equation

Posted on by John

The new book Heavenly Mathematics describes in the first chapter how the medieval scholar Abū Rayḥān al-Bīrūnī calculated the earth’s radius. The derivation itself is interesting, but here I want to expand on a parenthetical remark about the calculation.

The earth’s radius r can be found by solving the following equation.

\cos\theta = \frac{r}{r + 305.1m}

The constant in the denominator comes from a mountain which is 305.1 meters tall. The angle θ is known to be 34 minutes, i.e. 34/60 degrees. Here is the remark that caught my eye as someone more interested in numerical analysis than trigonometry:

There is a delicate matter hidden in this solution however: a minute change in the value of θ results in a large change in the value of r.

How can you tell that the solution is sensitive to changes (i.e. measurement errors) in θ? That doesn’t seem obvious.

Think of r as a function of θ and differentiate both sides of the equation with respect to θ. We’ll convert θ to radians because that’s what we do. (Explanation at the bottom of this post.) We get

-\sin\theta = \frac{305.1m}{(r + 305.1m)^2} \frac{dr}{d\theta}

or

\frac{dr}{d\theta} = -\sin\theta \frac{(r + 305.1m)^2}{305.1m}

Now let’s get a feel for the size of the terms in this equation. θ is approximately 0.01 radians, and so sin θ is approximately 0.01 as well. (See explanation here.) The radius of the earth is about 6.4 million meters. So the right side of the equation above is about 1.3 billion meters, i.e. it’s big.

A tiny increase in θ leads to a large decrease in r. For example, if our measurement of θ increased by 1%, from 0.01 to 0.0101, our measurement of the earth’s radius would decrease by 130,000 meters.

I’d like to point out a couple things about this analysis. First, it shows how it can be useful to think of constants as variables. After measuring θ we could think that we know its value with certainty and treat it as a constant. But a more sophisticated analysis takes into account that while θ might not change, our measurement of θ has changed from the true value.

Second, we used the radius of the earth to determine how sensitive our estimate of the earth’s radius is to changes in θ. Isn’t that circular reasoning? Not really. We can use a very crude estimate of the earth’s radius to estimate how sensitive a new estimate is to changes in its parameters. You always have some idea how big a value is before you measure it. If you want to measure the distance to the moon, you know not to pick up a yard stick.

Approximating Earth as a sphere

Posted on by John

Isaac Newton suggested in 1687 that the earth is not a perfectly round sphere but rather an ellipsoid, and he was right. But since our planet is roughly a sphere, it’s often useful to approximate it by a sphere. So if you’re going to do that, what radius do you use? More generally, what radius do you use when approximating any ellipsoid by a sphere?

This post will discuss the more general problem of finding the radius when approximating any ellipsoid by a sphere. We will give the answer for Earth in particular, and we’ll show how to carry out the calculations. Most of the calculations are easy, but some involve elliptic integrals and we show how to compute these in Python.

Ellipsoids and spheroids

First of all, what is an ellipsoid? It is a surface whose (x, y, z) coordinates satisfy

\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1

Earth is an oblate spheroid, which means a = b > c. Specifically, a = b = 6,378,137 meters, and c = 6,356,752 meters.

If you wanted to approximate an ellipsoid by a sphere, you could use

r = (a + b + c)/3.

Why? Because the knee-jerk reaction whenever you need to reduce a set of numbers to one number is to average them.

Volume of an ellipsoid

We could do a little better, depending on what property of the ellipsoid we’d like to preserve in our approximation. For example, we might want to create a sphere with the same volume as the ellipsoid. In that case we’d use the geometric mean

r = (abc)1/3.

This is because the volume of an ellipsoid is 4πabc/3 and the volume of a sphere is 4πr3/3.

For the particular case of the earth, we’d use

(a2c)1/3 = 6371000.7

Surface area of an ellipsoid

For some applications we might want a sphere with the same surface area as the ellipsoid rather than the same volume.

The surface area of an ellipsoid is considerably more complicated than the volume. For the special case of an oblate spheroid, like earth, the area is given by

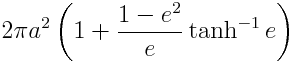
2\pi a^2 \left( 1 + \frac{1 - e^2}{e} \tanh^{-1}e \right)

where

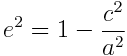
e^2 = 1 - \frac{c^2}{a^2}

The surface area of a sphere is 4 πr2 and so the following code computes r.

    from math import sqrt, atanh
    e = sqrt(1 - (c/a)**2)
    r = a*sqrt(1 + (1-e**2)*atanh(e)/e) / sqrt(2)

This gives r = 6371007.1 for the earth, about 6.4 meters more than the number we got matching volume rather than area.

For a general ellipsoid, the surface area is given by

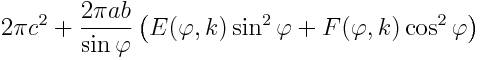
2\pi c^2 + \frac{2\pi a b}{\sin \varphi} \left( E(\varphi, k) \sin^2\varphi + F(\varphi, k) \cos^2 \varphi\right)

where

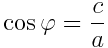
cos \varphi = \frac{c}{a}

and

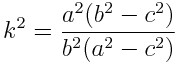
k^2 = \frac{a^2(b^2 - c^2)}{b^2(a^2 - c^2)}

Here F is the “incomplete elliptic integral of the first kind” and E is the “incomplete elliptic integral of the second kind.” The names are historical artifacts, but the “elliptic” part of name comes from the fact that these functions were discovered in the context of arc lengths with ellipses, so it shouldn’t be too surprising to see them here.

Computing ellipsoid surface area in Python

In SciPy, F(φ, k) is given by ellipkinc and E(φ, k) is given by ellipeinc. Both function names start with ellip because they are elliptic functions, and end in inc because they are “incomplete.” In the middle, ellipeinc has an “e” because it computes the mathematical function E(φ, k).

But why does ellipkinc have a “k” in the middle? The “complete” elliptic integral of the first kind is K(k) = F(π/2, k). The “k” in the function name is a reminder that we’re computing the incomplete version of the K function.

Here’s the code for computing the surface area of a general ellipsoid:

    from math import sin, cos, acos, sqrt, pi
    from scipy.special import ellipkinc, ellipeinc

    def area(a, b, c):
        phi = acos(c/a)
        k = a*sqrt(b**2 - c**2)/(b*sqrt(a**2 - c**2))
        E = ellipeinc(phi, k)
        F = ellipkinc(phi, k)
        elliptic = E*sin(phi)**2 + F*cos(phi)**2
        return 2.0*pi*c**2 + 2*pi*a*b*elliptic/sin(phi)

The differences between the various approximation radii are small for Earth. See my next post on elliptical galaxies where the differences are much larger.

More geodesy posts

Poor Mercator

Posted on by John

This morning’s xkcd cartoon is “What your favorite map projection says about you.” It’s really funny, but poor Mercator comes off as the most boring projection.

Mercator: You're not really into maps

Mercator is the most familiar projection, but it has some interesting properties. The most important is that lines of constant bearing on the Earth correspond to straight lines on the map, obviously a desirable property for navigation. More details here.

The inverse of the Mercator projection, going from maps onto the globe, is more interesting. Aside from its geographical importance, it gives a way of relating circular and hyperbolic functions without using complex numbers. More details here.

The Mercator projection is also historically interesting. The modern derivation of the Mercator projection uses logarithms and calculus, but Mercator came up with his projection in 1569 before logarithms or calculus had been discovered. (Update: See more historical detail in Thony C’s comment below.)

Angle of vertical: geocentric vs astronomical latitude

Posted on by John

Don Fredkin left a comment on my previous blog post that surprised me. I found out that latitude doesn’t exactly mean what I thought.

Imagine a line connecting your location with the center of the Earth. I thought that your latitude would be the angle that that line makes with the plane of the equator. And that’s almost true, but not quite.

Instead, you should imagine a line perpendicular to the Earth’s surface at your location and take the angle that that line makes with the plane of the equator.

If the Earth were perfectly spherical, the two lines would be identical and so the two angles would be identical. But since the Earth is an oblate spheroid (i.e. its cross-section is an ellipse) the two are not quite the same.

The angle I had in mind is the geocentric latitude ψ. The angle made by a perpendicular line and the plane of the equator is the geographic latitude φ, also known as the astronomical latitude. The following drawing from Wikipedia illustrates the difference, exaggerating the eccentricity of the ellipse.

How do these two ideas of latitude compare? I’ll sketch a derivation for equations relating geographic latitude φ and geocentric latitude ψ.

Let f(x, y) = (x/a)2 + (y/b)2 where a = 6378.1 km is the equatorial radius and b = 6356.8 km is the polar radius.. The gradient of f is perpendicular to the ellipse given by the level set f(x, y) = 1. At geocentric latitude ψ, y = tan(ψ) x and so the gradient is proportional to (1/a2, tan(ψ) / b2). From taking the dot product with (1, 0) it follows that the cosine of φ is given by

(1 + (a/b)4 tan2 ψ)-1/2.

It follows that

φ = tan-1( (a/b)2 tan ψ )

and

ψ = tan-1( (b/a)2 tan φ ).

The geocentric and geographic latitude are equal at the poles and equator. Between these extremes, geographic latitude is larger than geocentric latitude, but never by more than 0.2 degrees. The maximum difference, as you might guess, is near 45 degrees.

Here’s a graph of φ – ψ in degrees. The difference between these two angles is called the angle of vertical.

The maximum occurs at 44.9 degrees and equals 0.1917.

The curve looks very much like a parabola, and indeed it is. The approximation

φ = ψ + 0.186 – 0.0000946667 (ψ – 45)2

is very accurate, within about 0.005 degrees.

Related post: Journey away from the center of the Earth

Journey away from the center of the Earth

Posted on by John

What point on Earth is farthest from its center? Mt. Everest comes to mind, but its summit is the point highest above sea level, not the point farthest from the center. These are not the same because the Earth is not perfectly spherical.

Our planet bulges slightly at the equator due to its rotation. The equatorial diameter is about 0.3% larger than the polar diameter. Sea level at the equator is about 20 kilometers farther from the center of the Earth than sea level at the poles.

Chimborazo in Ecuador

Photo via Wikipedia

Mt. Everest is about nine kilometers above sea level and located about 28 degrees north of the equator. Chimborazo, the highest point in Ecuador, is seven kilometers above sea level and 1.5 degrees south of the equator.

So how far are Mt. Everest and Chimborazo from the center of the Earth? To answer that, we first need to how far sea level at latitude θ is from the center of the Earth.

Imagine slicing the Earth with a plane containing its polar diameter. To a good approximation (within 100 meters) the resulting shape would be an ellipse. The equation of this ellipse is

(x / a)2 + (y / b)2 = 1

where a = 6378.1 km is the equatorial radius and b = 6356.8 km is the polar radius. A line from the center of the ellipse to a point at latitude θ has equation y = tan(θ) x. Solving the pair of equations for x shows that the distance from the center to the point at latitude θ is

d = sqrt( a2b2 sec2 θ / (a2 tan2 θ + b2 ) )

For Mt. Everest, θ = 27.99 degrees and so d = 6373.4. For Chimborazo, θ = -1.486 degrees and so d = 6378.1. So sea level is 4.7 km higher at Chimborazo. Mt. Everest is 2.6 km taller, but the summit of Chimborazo is about 2.1 km farther away from the center of the Earth.

Update: See my next post for a slight correction. A more accurate calculation would compute sea level is about 4.65 km higher at Chimborazo than Mt. Everest.

More geodesy