Bayesian

A Bayesian approach to proving you’re human

Posted on by John

I set up a GitHub account for a new employee this morning and spent a ridiculous amount of time proving that I’m human.

The captcha was to listen to three audio clips at a time and say which one contains bird sounds. This is a really clever test, because humans can tell the difference between real bird sounds and synthesized bird-like sounds. And we’re generally good at recognizing bird sounds even against a background of competing sounds. But some of these were ambiguous, and I had real birds chirping outside my window while I was doing the captcha.

You have to do 20 of these tests, and apparently you have to get all 20 right. I didn’t. So I tried again. On the last test I accidentally clicked the start-over button rather than the submit button. I wasn’t willing to listen to another 20 triples of audio clips, so I switched over to the visual captcha tests.

These kinds of tests could be made less annoying and more secure by using a Bayesian approach.

Suppose someone solves 19 out of 20 puzzles correctly. You require 20 out of 20, so you have them start over. When you do, you’re throwing away information. You require 20 more puzzles, despite the fact that they only missed one. And if a bot had solved say 8 out of 20 puzzles, you’d let it pass if it passes the next 20.

If you wipe your memory after every round of 20 puzzles, and allow unlimited do-overs, then any sufficiently persistent entity will almost certainly pass eventually.

Bayesian statistics reflects common sense. After someone (or something) has correctly solved 19 out of 20 puzzles designed to be hard for machines to solve, your conviction that this entity is human is higher than if they/it had solved 8 out of 20 correctly. You don’t need as much additional evidence in the first case as in the latter to be sufficiently convinced.

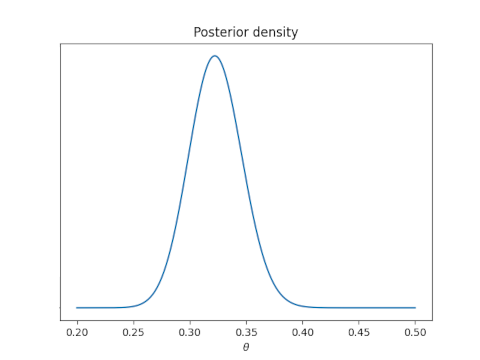
Here’s how a Bayesian captcha could work. You start out with some distribution on your probability θ that an entity is human, say a uniform distribution. You present a sequence of puzzles, recalculating your posterior distribution after each puzzle, until the posterior probability that this entity is human crosses some upper threshold, say 0.95, or some lower threshold, say 0.50. If the upper threshold is crossed, you decide the entity is likely human. If the lower threshold is crossed, you decide the entity is likely not human.

If solving 20 out of 20 puzzles correctly crosses your threshold of human detection, then after solving 19 out 20 correctly your posterior probability of humanity is close to the upper threshold and would only require a few more puzzles. And if an entity solved 8 out of 20 puzzles correctly, that may cross your lower threshold. If not, maybe only a few more puzzles would be necessary to reject the entity as non-human.

When I worked at MD Anderson Cancer Center we applied this approach to adaptive clinical trials. A clinical trial might stop early because of particularly good results or particularly bad results. Clinical trials are expensive, both in terms of human costs and financial costs. Rejecting poor treatments quickly, and sending promising treatments on to the next stage quickly, is both humane and economical.

Related posts

Beta approximation to binomial

Posted on by John

It is well-known that you can approximate a binomial distribution with a normal distribution. Of course there are a few provisos …

Robin Williams imitating William F. Buckley

It is also well-known that you can approximate a beta distribution with a normal distribution as well.

This means you could directly approximate a binomial distribution with a beta distribution. This is a trivial consequence of the two other approximation results, but I don’t recall seeing this mentioned anywhere.

Why would you want to approximate a binomial distribution with a beta? The normal distribution is better known than the beta, and the normal approximation is motivated by the central limit theorem. However, approximating a binomial distribution by a beta makes the connection to Bayesian statistics clearer.

Let’s look back at a post I wrote yesterday. There I argued that the common interpretation of a confidence interval, while unjustified by the theory that produced it, could be justified by appealing to Bayesian statistics because a frequentist confidence interval, in practice, is approximately a Bayesian credible interval.

In that post I give an example of estimating a proportion p based on a survey with 127 positive responses out of 400 persons surveyed. The confidence interval given in that post implicitly used a normal approximation to a binomial. This is done so often that it typically goes unnoticed, and it is justified for large samples when p is not too close to 0 or 1.

Binomial distributions with large n are difficult to work with and it is more convenient to work with continuous distributions. Instead of the normal approximation, we could have used a beta approximation. This has nothing to do with Bayesian statistics yet. We could introduce the beta distribution simply as an alternative to the normal distribution.

The distribution on the estimated rate is binomial with p = 127/400 and variance p(1-p)/n with n = 400.

We could compare this to a beta distribution with the same mean and variance. I worked out here how to solve beta distribution parameters that lead to a specified mean and variance. If we do that with the mean and variance above we get a = 126.7 and b = 272.3. We could then find a 95% confidence interval by finding the 2.5 and 97.5 percentiles for a beta(126.7, 272.3) distribution. When we do, we get a confidence interval of (0.2728, 0.3639), very nearly what we got in the earlier post using a normal approximation.

At this point we have been doing frequentist statistics, using a beta distribution as a computational convenience. Now let’s put on our Bayesian hats. Starting with a uniform, i.e. beta(1, 1), prior, we get a posterior distribution on the proportion we’re estimating which has a beta(128, 274).

If you plot the density functions of a beta(126.7, 272.3) and a beta(128, 274) you’ll see that they agree to within the thickness of a line.

Related posts

Can you have confidence in a confidence interval?

Posted on by John

“The only use I know for a confidence interval is to have confidence in it.” — L. J. Savage

Can you have confidence in a confidence interval? In practice, yes. In theory, no.

If you have a 95% confidence interval for a parameter θ, can you be 95% sure that θ is in that interval? Sorta.

Frequentist theory

According to frequentist theory, parameters such as θ are fixed constants, though unknown. Probability statements about θ are forbidden. Here’s an interval I. What is the probability that θ is in I? Well, it’s 1 if θ is in the interval and 0 if it is not.

In theory, the probability associated with a confidence interval says something about the process used to create the interval, not about the parameter being estimated. Our θ is an immovable rock. Confidence intervals come and go, some containing θ and others not, but we cannot make probability statements about θ because θ is not a random variable.

Here’s an example of a perfectly valid and perfectly useless way to construct a 95% confidence interval. Take an icosahedron, draw an X on one face, and leave the other faces unmarked. Roll this 20-sided die, and if the X comes up on top, return the empty interval. Otherwise return the entire real line.

The resulting interval, either ø or (-∞, ∞), is a 95% confidence interval. The interval is the result of a process which will contain the parameter θ 95% of the time.

Now suppose I give you the empty set as my confidence interval. What is the probability now that θ is in the empty interval? Zero. What if I give you the real line as my confidence interval. What is the probability that θ is in the interval? One. The probability is either zero or one, but in no case is it 0.95. The probability that a given interval produced this way contains θ is never 95%. But before I hand you a particular result, the probability that the interval will be one that contains θ is 0.95.

Bayesian theory

Confidence intervals are better in practice than the example above. And importantly, frequentist confidence intervals are usually approximately Bayesian credible intervals.

In Bayesian statistics you can make probability statements about parameters. Once again θ is some unknown parameter. How might we express our uncertainty about the value of θ? Probability! Frequentist statistics represents some forms of uncertainty by probability but not others. Bayesian statistics uses probability to model all forms of uncertainty.

Example

Suppose I want to know what percentage of artists are left handed and I survey 400 artists. I find that 127 of artists surveyed were southpaws. A 95% confidence interval, using the most common approach rather than the pathological approach above, is given by

\left(\hat{p} - z_{1-\alpha/2} \sqrt{\frac{\hat{p}\hat{q}}{n}}, \hat{p} + z_{1-\alpha/2} \sqrt{\frac{\hat{p}\hat{q}}{n}} \right)

This results in a confidence interval of (0.272, 0.363).

Now suppose we redo our analysis using a Bayesian approach. Say we start with a uniform prior on θ. Then the posterior distribution on θ will have a beta(128, 264) distribution.

Now we can say in clear conscience that there is a 94% posterior probability that θ is in the interval (0.272, 0.363).

There are a couple predictable objections at this point. First, we didn’t get exactly 95%. No, we didn’t. But we got very close.

Second, the posterior probability depends on the prior probability. However, it doesn’t depend much on the prior. Suppose you said “I’m pretty sure most people are right handed, maybe 9 out of 10, so I’m going to start with a beta(1, 9) prior.” If so, you would compute the probability of θ being in the interval (0.272, 0.373) to be 0.948. Your a priori knowledge led you to have a little more confidence a posteriori.

Commentary

The way nearly everyone interprets a frequentist confidence interval is not justified by frequentist theory. And yet it can be justified by saying if you were to treat it as a Bayesian credible interval, you’d get nearly the same result.

You can often justify an informal understanding of frequentist statistics on Bayesian grounds. Note, however, that a Bayesian interpretation would not rescue the 95% confidence interval that returns either the empty set or the real line.

Often frequentist and Bayesian analyses reach approximately the same conclusions. A Bayesian can view frequentist techniques as convenient ways to produce approximately correct Bayesian results. And a frequentist can justify using a Bayesian procedure because the procedure has good frequentist properties.

There are times when frequentist and Bayesian results are incompatible, and in that case the Bayesian results typically make more sense in my opinion. But very often other considerations, such as model uncertainty, are much more substantial than the difference between a frequentist and Bayesian analysis.

Related posts

First names and Bayes’ theorem

Posted on by John

Is the woman in this photograph more likely to be named Esther or Caitlin?

black and white photo of an elderly woman

Yesterday Mark Jason Dominus published wrote about statistics on first names in the US from 1960 to 2021. For each year and state, the data tell how many boys and girls were given each name.

Reading the data “forward” you could ask, for example, how common was it for girls born in 1960 to be named Paula. Reading the data “backward” you could ask how likely it is that a woman named Paula was born in 1960.

We do this intuitively. When you hear a name like Blanche you may think of an elderly woman because the name is uncommon now (in the US) but was more common in the past. Sometimes we get a bimodal distribution. Olivia, for example, has made a comeback. If you hear that a female is named Olivia, she’s probably not middle aged. She’s more likely to be in school or retired than to be a soccer mom.

Bayes’ theorem tells us how to turn probabilities around. We could go through Mark’s data and compute the probabilities in reverse. We could quantify the probability that a woman named Paula was born in the 1960s, for example, by adding up the probabilities that she was born in 1960, 1961, …, 1969.

Bayes theorem says

P(age | name) = P(name | age) P(age) / P(name).

Here the vertical bar separates the thing we want the probability of from the thing we assume. P(age | name), for example, is the probability of a particular age, given a particular name.

There is no bar in the probability in the denominator above. P(name) is the overall probability of a particular name, regardless of age.

People very often get probabilities backward; they need Bayes theorem to turn them around. A particular case of this is the prosecutor’s fallacy. In a court of law, the probability of a bit of evidence given that someone is guilty is irrelevant. What matters is the probability that they are guilty given the evidence.

In a paternity case, we don’t need to know the probability of someone having a particular genetic marker given that a certain man is or is not their father. We want to know the probability that a certain man is the father, given that someone has a particular genetic marker. The former probability is not what we’re after, but it is useful information to stick into Bayes’ theorem.

Related posts

Photo by Todd Cravens on Unsplash.

A Bayesian approach to pricing

Posted on by John

Suppose you want to determine how to price a product and you initially don’t know what the market is willing to pay. This post outlines some of the things you might think about, and how Bayesian modeling might help.

This post is not the final word on the subject, or even my final word on the subject. It is essentially a reply to a friend’s question turned into a blog post rather than an email.

Prior information

You must have some idea, however vague, what the market value of your product is. If you had absolutely no idea what a product is worth, you wouldn’t be considering it as a business opportunity.

There is always prior information. As a former colleague would say, when you want to measure the distance to the moon, you know not to pick up a yard stick. Whenever you do an experiment, something motivated you to do the experiment.

This is an ideal application of Bayesian statistics because you have valuable prior information before you have data. Until you have a moderate amount of data, your prior information may be more useful than your data.

Some people will say you should only act on data, not on subjective prior knowledge, but this is impossible. When you offer your product for the first time, you have no data. All you have to go on is prior information. You could hide your prior information in the design of an experiment rather than making it explicit in a prior distribution, but it’s still there.

Model

Assume the market price for some product can be modeled by a random variable X that depends on some parameter θ. I’m not saying that the price is random in any philosophical sense, only that it is useful to model it as random. More on this line of thinking here.

By modeling market price as a random variable rather than a single number, we’re acknowledging that it has some fuzziness to it. Different customers are willing to pay different amounts for the same product. Maybe the prices they’re willing to pay are tightly distributed around some center, or maybe there’s substantial variance.

When we make a sale, or fail to make a sale, we learn something about θ. But notice that we don’t observe X per se, we observe whether a particular sample from X was above or below the offer price. You’re not conducting a survey where you ask “What is the highest price p that you’d be willing to pay” and get a candid answer. You make an offer x, and it is either accepted or rejected. You observe whether x < p or x > p.

This means the likelihood function is similar to what you’d see in modeling survival data, but a little different. When someone dies, you fully observe their survival time. But if you follow up with someone and they’re still alive, you only know a lower bound on their survival time, not the survival time itself. We say the data is censored because we haven’t yet observed everything we want to know.

Survival data is usually asymmetric, censored on one side but not the other. You could have two-sided censoring, but that’s less common.

With pricing your data is always censored in both directions. You either get a lower bound or an upper bound on what someone would have been willing to pay.

After each offer and response, you can update your estimate of θ. Each interaction gives you a better idea of the distribution on θ.

Pricing

Now suppose after numerous observations you’re moderately confident in your knowledge of θ. Now what?

One response is “Well then you charge what the market is most likely to bear.” That’s kind of a simplistic optimization. It implicitly assumes you’re OK with a 50% chance of a sale going through. Maybe your business is struggling and you don’t have many leads. Then you want a higher conversion rate. Or maybe you’re doing well, have plenty leads, and are OK with a low conversion rate. This is especially the case if the distribution on market price has a lot of variance; if the variance is low it makes more sense to think of “the” price as if it were a single number.

So far I have implicitly assumed that the only consequence of asking too much is a lost sale. But if you ask for too much, you might lose future sales, even if you get the current sale. I’ve also assumed that customers always prefer lower prices. That’s not the case. Asking too little for a product can hurt your credibility, for example.

Estimating willingness to pay is complicated, and determining what to do once you’ve made that estimate is complicated as well. This post is just a sketch of the thought process a company might go through.

Related posts

Universal confidence interval

Posted on by John

Here’s a way to find a 95% confidence interval for any parameter θ.

  • With probability 0.95, return the real line.
  • With probability 0.05, return the empty set.

Clearly 95% of the time this procedure will return an interval that contains θ.

This example shows the difference between a confidence interval and a credible interval.

A 95% credible interval is an interval such that the probability is 95% that the parameter is in the interval. That’s what people think a 95% confidence interval is, but it’s not.

Suppose I give you a confidence interval using the procedure above. The probability that θ is in the interval is 1 if I return the real line and 0 if I return the empty set. In either case, the interval that I give you tells you absolutely nothing about θ.

But if I give you a 95% credible interval (a, b), then given the model and the data that went into it, the probability is 95% that θ is in the interval (a, b).

Confidence intervals are more useful in practice than in theory because they often approximately correspond to a credible interval under a reasonable model.

Credible intervals depend on your modeling assumptions. So do confidence intervals.

Confidence interval widths

Posted on by John

Suppose you do N trials of something that can succeed or fail. After your experiment you want to present a point estimate and a confidence interval. Or if you’re a Bayesian, you want to present a posterior mean and a credible interval. The numerical results hardly differ, though the two interpretations differ.

If you got half successes, you will report a confidence interval centered around 0.5. The more unbalanced your results were, the smaller your confidence interval will be. That is, the confidence interval will be smallest if you had no successes and widest if you had half successes.

What can we say about how the width of your confidence varies as a function of your point estimate p? That question is the subject of this post [1].

Frequentist confidence interval width

We’ll start with an example, where N = 1,000,000. We let our number of observed successes n vary from 0 to 500,000 and plot the width of a 95% confidence interval as a function of n on a log-log plot. (By symmetry we only need to look to up to N/2. If you have more than half successes, reverse your definitions of success and failure.)

The result is almost a perfectly straight line, with the exception of a tiny curve at the end. This says the log of the confidence interval is a linear function of the log of n, or in other words, the dependence of confidence interval width on n follows a power law.

Bayesian credible interval width

The plot above measures frequentist confidence intervals, using Wilson score with continuity correction. We can repeat our experiment, putting on our Bayesian hat, and compute credible intervals using a Jeffreys prior, that is, a beta(0.5, 0.5) prior.

The results are indistinguishable. The confidence interval widths differ after the sixth decimal place.

In this example, there’s very little quantitative difference between a frequentist confidence interval and a Bayesian credible interval. The difference is primarily one of interpretation. The Bayesian interpretation makes sense and the frequentist interpretation doesn’t [2].

Power law

If the logs of two things are related linearly [3], then the things themselves are related by a power law. So if confidence/credible interval width varies as a power law with the point estimate p, what is that power law?

The plots above suggest that to a good approximation, if we let w be the credible interval length,

log w = m log p + b

for some slope m and intercept b.

We can estimate the slope by choosing p = 10-1 and p = 10-5. This gives us m = 0.4925 and b = -5.6116. There are theoretical reasons to expect that m should be 0.5, so we’ll round 0.4925 up to 0.5 both for convenience and for theory.

So

log w = 0.5 log p – 5.6116.

and so

w = 0.00366 √p

Let’s see how well this works by comparing it to the exact interval length. (I’m using Jeffreys’ credible interval, not that it matters.)

The power law approximation works well when the estimated proportion p is small, say less than 0.2. For larger p the normal approximation works well.

We could have guessed that the confidence interval width was proportional to √p(1-p) based on the normal approximation/central limit theorem. But the normal approximation is not uniformly good over the range of all ps.

Related posts

[1] Standard notation would put a little hat on top of the p but HTML doesn’t make this possible without inserting images into text. I hope you don’t mind if I take my hat off.

[2] This quip is a little snarky, but it’s true. When I would ask graduate students to describe what a confidence interval is, they would basically give me the definition of a credible interval. Most people who calculate frequentist confidence intervals think they’re calculating Bayesian credible intervals, though they don’t realize it. The definition of confidence interval is unnatural and convoluted. But confidence intervals work better in practice than in theory because they approximate credible intervals.

L. J. Savage once said

“The only use I know for a confidence interval is to have confidence in it.”

In other words, the value of a confidence interval is that you can often get away with interpreting it as a credible interval.

[3] Unfortunately the word “linear” is used in two inconsistent ways. Technically we should say “affine” when describing a function y = mx + b, and I wish we would. But that word isn’t commonly known. People call this relation linear because the graph is a line. Which makes sense, but it’s inconsistent with the use of “linear” as in “linear algebra.”

 

Scaled Beta2 distribution

Posted on by John

I recently ran across a new probability distribution called the “Scaled Beta2” or “SBeta2” for short in [1].

For positive argument x and for positive parameters p, q, and b, its density is

\frac{\Gamma(p+q)}{b\,\Gamma(p) \, \Gamma(q)}\, \frac{\left(\frac{x}{b}\right)^{p-1}}{\left(\left(\frac{x}{b}\right) + 1 \right)^{p+q}}

This is a heavy-tailed distribution. For large x, the probability density is O(x–q-1), the same as a Student-t distribution with q degrees of freedom.

The authors in [1] point out several ways this distribution can be useful in application. It can approximate a number of commonly-used prior distributions while offering advantages in terms of robustness and analytical tractability.

Related posts

[1] The Scaled Beta2 Distribution as a Robust Prior for Scales. María-Eglée Pérez, Luis Raúl Pericchi, Isabel Cristina Ramírez. Available here.

Predictive probability for large populations

Posted on by John

Suppose you want to estimate the number of patients who respond to some treatment in a large population of size N and what you have is data on a small sample of size n.

The usual way of going about this calculates the proportion of responses in the small sample, then pretends that this is the precisely known proportion, and applies it to the population as a whole. This approach underestimates the uncertainty in the final estimate because it ignores the uncertainty in the initial estimate.

A more sophisticated approach creates a distribution representing what is known about the proportion of successes based on the small sample and any prior information. Then it estimates the posterior predictive probability of outcomes in the larger population based on this distribution. For more background on predictive probability, see my post on uncertainty in a probability.

This post will look at ways to compute predictive probabilities using the asymptotic approximation presented in the previous post.

Suppose your estimate on the probability of success, based on your small sample and prior information, has a Beta(α, β) distribution. Then the predictive probability of s successes and f failures is

{s + f \choose s} \frac{B(s + \alpha, f + \beta)}{B(\alpha, \beta)}

The beta functions in the numerator and denominator are hard to understand and hard to compute, so we would like to replace them with something easier to understand and easier to compute.

We begin by expanding all the terms involving s and f in terms of gamma functions.

\frac{1}{B(\alpha,\beta)} \frac{\Gamma(s+f+1)}{\Gamma(s+1)\, \Gamma(f+1)} \frac{\Gamma(s+\alpha)\, \Gamma(f+\beta)}{\Gamma(s+f+\alpha+\beta)}

By rearranging the terms we can see three examples of the kind of gamma function ratios estimated in the previous post.

\frac{1}{B(\alpha,\beta)} \frac{\Gamma(s+\alpha)}{\Gamma(s+1)} \frac{\Gamma(f+\beta)}{\Gamma(f+1)} \frac{\Gamma(s+f+1)}{\Gamma(s+f+\alpha+\beta)}

Now we can apply the simplest approximation from the previous post to get the following.

\frac{s^{\alpha-1} f^{\beta-1} (s +f)^{1 - \alpha-\beta-1}}{B(\alpha, \beta)}

We can make this approximation more symmetric by expanding Beta(α, β) in terms of factorials:

\frac{(\alpha + \beta-1)!}{(\alpha-1)!\, (\beta-1)!} \,\,\frac{s^{\alpha-1} f^{\beta-1}}{(s+f)^{\alpha+\beta-1}}

We saw in the previous post that we can make our asymptotic approximation much more accurate by shifting the arguments a bit, and the following expression, while a little more complicated, should be more accurate.

\frac{(\alpha + \beta-1)!}{(\alpha-1)!\, (\beta-1)!} \,\, \frac{ \left(s + \tfrac{\alpha}{2}\right)^{\alpha-1} \left(f + \tfrac{\beta}{2}\right)^{\beta-1} }{ \left(s +f + \tfrac{\alpha+\beta}{2}\right)^{\alpha+\beta-1} }

This should be accurate for sufficiently large s and f, but I haven’t tested it numerically and wouldn’t recommend using it without doing some testing first.

Automatic data reweighting

Posted on by John

Suppose you are designing an autonomous system that will gather data and adapt its behavior to that data.

At first you face the so-called cold-start problem. You don’t have any data when you first turn the system on, and yet the system needs to do something before it has accumulated data. So you prime the pump by having the system act at first on what you believe to be true prior to seeing any data.

Now you face a problem. You initially let the system operate on assumptions rather than data out of necessity, but you’d like to go by data rather than assumptions once you have enough data. Not just some data, but enough data. Once you have a single data point, you have some data, but you can hardly expect a system to act reasonably based on one datum.

Rather than abruptly moving from prior assumptions to empirical data, you’d like the system to gradually transition from reliance on the former to reliance on the latter, weaning the system off initial assumptions as it becomes more reliant on new data.

The delicate part is how to manage this transition. How often should you adjust the relative weight of prior assumptions and empirical data? And how should you determine what weights to use? Should you set the weight given to the prior assumptions to zero at some point, or should you let the weight asymptotically approach zero?

Fortunately, there is a general theory of how to design such systems. It’s called Bayesian statistics. The design issues raised above are all handled automatically by Bayes theorem. You start with a prior distribution summarizing what you believe to be true before collecting new data. Then as new data arrive, the magic of Bayes theorem adjusts this distribution, putting more emphasis on the empirical data and less on the prior. The effect of the prior gradually fades away as more data become available.

Related posts