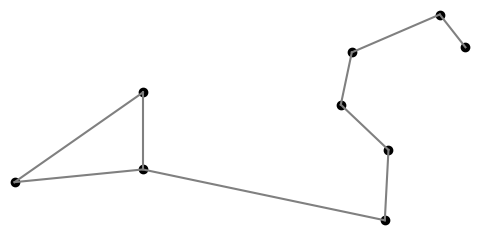
The p-norm of a vector is defined to be the pth root of the sum of its pth powers.

Such norms occur frequently in application [1]. Yoshio Koide discovered in 1981 that if you take the masses of the electron, muon, and tau particles, the ratio of the 1 norm to the 1/2 norm is very nearly 2/3. Explicitly,

to at least four decimal places. Since the ratio is tantalizingly close to 2/3, some believe there’s something profound going on here and the value is exactly 2/3, but others believe it’s just a coincidence.
The value of 2/3 is interesting for two reasons. Obviously it’s a small integer ratio. But it’s also exactly the midpoint between the smallest and largest possible value. More on that below.
Is the value 2/3 within the measure error of the constants? We’ll investigate that with a little Python code.
Python code
The masses of particles are available in the physical_constants dictionary in scipy.constants. For each constant, the dictionary contains the best estimate of the value, the units, and the uncertainty (standard deviation) in the measurement [2].
from scipy.constants import physical_constants as pc
from scipy.stats import norm
def pnorm(v, p):
return sum(x**p for x in v)**(1/p)
def f(v):
return pnorm(v, 1) / pnorm(v, 0.5)
m_e = pc["electron mass"]
m_m = pc["muon mass"]
m_t = pc["tau mass"]
v0 = [m_e[0], m_m[0], m_t[0]]
print(f(v0))
This says that the ratio of the 1 norm and 1/2 norm is 0.666658, slightly less than 2/3. Could the value be exactly 2/3 within the resolution of the measurements? How could we find out?
Measurement uncertainty
The function f above is minimized when its arguments are all equal, and maximized when its arguments are maximally unequal. To see this, note that f(1, 1, 1) = 1/3 and f(1, 0, 0) = 1. You can prove that those are indeed the minimum and maximum values. To see if we can make f larger, we want to increase the largest value, the mass of tau, and decrease the others. If we move each value one standard deviation in the desired direction, we get
v1 = [m_e[0] - m_e[2],
m_m[0] - m_m[2],
m_t[0] + m_t[2]]
print(f(v1))
which returns 0.6666674, just slightly bigger than 2/3. Since the value can be bigger than 2/3, and less than 2/3, the intermediate value theorem says there are values of the constants within one standard deviation of their mean for which we get exactly 2/3.
Now that we’ve shown that it’s possible to get a value above 2/3, how likely is it? We can do a simulation, assuming each measurement is normally distributed.
N = 1000
above = 0
for _ in range(N):
r_e = norm(m_e[0], m_e[2]).rvs()
r_m = norm(m_m[0], m_m[2]).rvs()
r_t = norm(m_t[0], m_t[2]).rvs()
t = f([r_e, r_m, r_t])
if t > 2/3:
above += 1
print(above)
When we I ran this, I got 168 values above 2/3 and the rest below. So based solely on our calculations here, not taking into account any other information that may be important, it’s plausible that Koide’s ratio is exactly 2/3.
***
[1] Strictly speaking, we should take the absolute values of the vector components. Since we’re talking about masses here, I simplified slightly by assuming the components are non-negative.
Also, what I’m calling the p “norm” is only a norm if p is at least 1. Values of p less than 1 do occur in application, even though the functions they define are not norms. I’m pretty sure I’ve blogged about such an application, but I haven’t found the post.
[2] The SciPy library obtained its values for the constants and their uncertainties from the CODATA recommended values, published in 2014.