Here’s something I do all the time. I have a function of one variable and several parameters. I implement it as a function object in C++ so I can pass it on to code that does something with functions of one variable, such as integration or optimization. I’ll give a trivial example and then show the most recent real problem I’ve worked on.
Say I have a function f(x; a, b, c) = 1000a + 100b + 10c + x. In a sense this is simply a function of four variables. But the connotation of using a semicolon rather than a comma after the x is that I think of x as being a variable and I think of a, b, and c as parameters. So f is a function of one variable that depends on three constants. (A “parameter” is a “constant” that can change!)
I create a C++ function object with two methods. One method is a constructor that takes the function parameters as arguments and saves them to member variables. The other method is an overload of the parenthesis method. That’s what makes the class a function object. By overloading the parenthesis method, I can call an instance of the class as if it were a function. Here’s some code.
class FunctionObject
{
public:
FunctionObject(double a, double b, double c)
{
m_a = a;
m_b = b;
m_c = c;
}
double operator()(double x) const
{
return 1000*m_a + 100*m_b + 10*m_c + x;
}
private:
double m_a;
double m_b;
double m_c;
};
So maybe I instantiate an instance of this function object and pass it to a function that finds the maximum value over an interval [a, b]. The code might look like this.
FunctionObject f(3, 1, 4);
double maximum = Maximize(f, a, b);
Here’s a more realistic example. A few days ago I needed to solve this problem. Given user input parameters λ, σ, n, and ξ, find b such that the following holds.
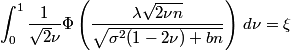
The function Φ above is the CDF of a standard normal random variable, defined here.
To solve this problem, I wrote a function object to evaluate the left side of the equation above. It takes λ, σ, and n as constructor arguments and takes b as an argument to operator(). Then I passed the function object to a root-finding method to solve for the value of b that makes the function value equal ξ. But my function is defined in terms of an integral, so I needed to write another function object first that returns the integrand. Then I pass that function object to this numerical integration routine. So I had to write two function objects to solve this problem.
There are several advantages to function objects over functions. For example, I would typically do parameter validation in the constructor. Quite often I also do some expensive calculations in the constructor and cache the results so that each call to operator() is then more efficient. Maybe I want to keep track of how often the function is called, so I put in some sort of odometer method that increments a counter with each call.
Unfortunately there’s a fair amount of code to write in order to implement even the simplest function. This effort hardly matters in production code; so many other things take more time. But it is annoying when doing some quick exploration. The next post shows how this can be done much easier in Python. The Python approach would be much easier for small problems, but it doesn’t have the advantages mentioned above such as caching expensive calculations in a constructor.