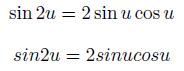There’s a law of large numbers, a law of small numbers, and a law of medium numbers in between.
The law of large numbers is a mathematical theorem. It describes what happens as you average more and more random variables.
The law of small numbers is a semi-serious statement about how people underestimate the variability of the average of a small number of random variables.
The law of medium numbers is a term coined by Gerald Weinberg in his book An Introduction to General Systems Thinking. He states the law as follows.
For medium number systems, we can expect that large fluctuations, irregularities, and discrepancy with any theory will occur more or less regularly.
The law of medium numbers applies to systems too large to study exactly and too small to study statistically. For example, it may be easier to understand the behavior of an individual or a nation than the dynamics of a small community. Atoms are simple, and so are stars, but medium-sized things like birds are complicated. Medium-sized systems are where you see chaos.
Weinberg warns that medium-sized systems challenge science because scientific disciplines define their boundaries by the set of problems they can handle. He says, for example, that
Mechanics, then, is the study of those systems for which the approximations of mechanics work successfully.
He warns that we should not be mislead by a discipline’s “success with systems of its own choosing.”
Weinberg’s book was written in 1975. Since that time there has been much more interest in the emergent properties of medium-sized systems that are not explained by more basic sciences. We may not understand these systems well, but we may appreciate the limits of our understanding better than we did a few decades ago.