This is the third in a series of four blog posts on mechanical vibrations. The first two posts were
- Part I: Introduction and free undamped vibrations
- Part II: Free undamped vibrations
We’re looking at solutions to the differential equation
m u'' + γ u' + k u = F cos ωt
The first two posts considered “free” vibrations, systems with no external input. The coefficient F is zero in such systems. Now we consider the effect of an external driving force of the form F cos ωt. We’ll leave out damping effects in this post, that is, we will assume γ = 0. The final post in this series will cover damped, driven oscillations, i.e. the case of γ and F both positive.
When the right-hand side of a linear differential equation is 0, we say the equation is homogeneous. When the right-hand side is not zero, we say the equation is non-homogeneous.
The general solution to a non-homogeneous linear differential equation is the general solution to the corresponding homogeneous equation plus any particular solution to the non-homogeneous equation. That is, all we have to do is find one solution to the equation with the forcing term, and add it to the general solution to the equation without the forcing term.
Recall that the natural frequency of our equation without forcing is ω defined by
ω02 = k/m.
and that the general solution without forcing is
u(t) = R cos(ω0t – φ)
where the amplitude R and the phase φ are determined by the initial conditions. To find the general solution to the non-homogeneous we need to find one solution to the non-homogeneous equation, and here’s one:
F cos(ωt) /(m(ω02 – ω2))
provided that the natural frequency ω0 is not equal to the driving frequency ω. This says that the general solution is the sum of two periodic functions, one with the natural frequency ω0 and one with the frequency of the driving force ω. In general, the sum of two periodic functions can be fairly complicated, and not necessarily periodic. More on that here.
Next we will look at two phenomena that the solutions can illustrate: beats and resonance. The latter happens when the natural and driving frequencies are equal.
Beats
If the starts at position 0 and with velocity 0, then the amplitudes of the homogeneous and non-homogeneous solutions are the same. The solution is
F /(m(ω02 – ω2)) ( cos(ωt) – cos(ω0t) )
We can apply the trig identity
cos(A) – cos(B) = 2 sin( (A–B)/2 ) sin(( A+B)/2 )
to rewrite the solution as the amplitude 2F /(m(ω02 – ω2)) times
sin( (ω0 – ω) t/2 ) sin( (ω0 + ω) t/2 )
If the natural and driving frequencies are similar, i.e. |ω0 – ω| is small, then the first term is a low frequency factor multiplying the second high frequency term. This phenomena is known as beats. You can hear it, for example, when two instruments are nearly but not quite in tune. If one is playing an A 440 and the other an A 441, you’ll hear a pitch of 440.5 getting louder and softer at a frequency of one cycle per second.
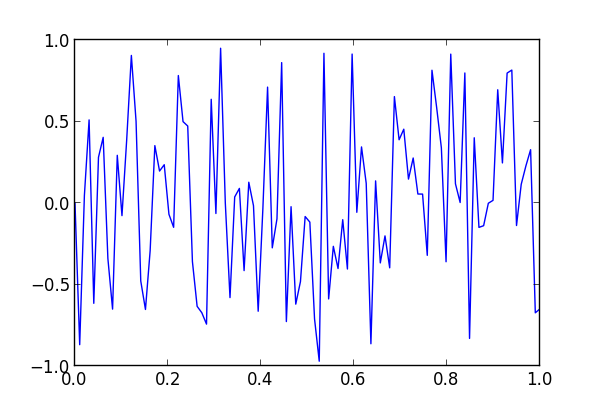
Here’s an example of beats, plotting sin(t) sin(10t). The solid blue line is the product. The dotted green lines are sin(t) and -sin(t).
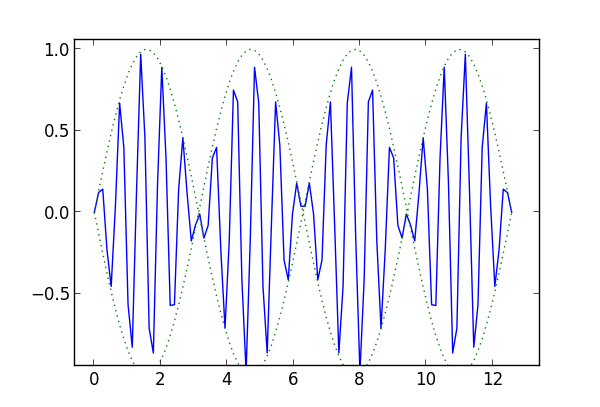
Incidentally, this is related to how AM radio works: the broadcast content is multiplied by the carrier wave.
Resonance
When we wrote down the solution above, we assumed the natural and driving frequencies were not equal. If they are, if the system is being driven at its natural frequency, we have resonance. In that case, the solution to the non-homogeneous equation is
(F/2mω) t sin ωt.
Because the solution is proportional to t sin ωt, this says we have oscillations whose amplitude grows linearly with time. In theory, the oscillations can become arbitrarily large. In reality there is always some damping, which eventually puts some limit on the amplitude of the oscillations. Also, the system may break before damping would reign in the oscillations.
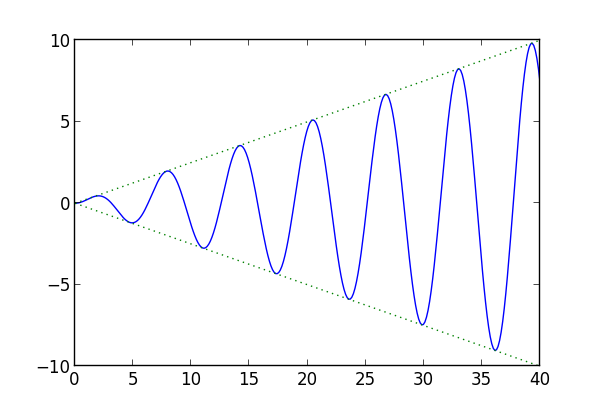
Here’s an example of resonance, plotting 0.25 t sin(t) in solid blue and ± 0.25 t in dotted green.
Next
The final post in this series will look at the effect of damping on forced vibrations.
For daily posts about differential equations, follow @diff_eq on Twitter.