This post will look at two numerical integration methods, the trapezoid rule and Romberg’s algorithm, and memoization. This post is a continuation of ideas from the recent posts on Lobatto integration and memoization.

Although the trapezoid rule is not typically very accurate, it can be in special instances, and Romberg combined it with extrapolation to create a very accurate method.

Trapezoid rule

The trapezoid is the simplest numerical integration method. The only thing that could be simpler is Riemann sums. By replacing rectangles of Riemann sums with trapezoids, you can make the approximation error an order of magnitude smaller.

The trapezoid rule is crude, and hardly recommended for practical use, with two exceptions. It can be remarkably efficient for periodic functions and for analytic functions that decay double exponentially. The trapezoid rule works so well in these cases that it’s common to transform a general function so that it has one of these forms so the trapezoid rule can be applied.

To be clear, the trapezoid rule for a given step size h may not be very accurate. But for periodic and double exponential functions the error decreases exponentially as h decreases.

Here’s an implementation of the trapezoid rule that follows the derivation directly.

    def trapezoid1(f, a, b, n):
        integral = 0
        h = (b-a)/n
        for i in range(n):
            integral += 0.5*h*(f(a + i*h) + f(a + (i+1)*h))
        return integral

This code approximates the integral of f(x) over [a, b] by adding up the areas of n trapezoids. Although we want to keep things simple, a slight change would make this code twice as efficient.

    def trapezoid2(f, a, b, n):
        integral = 0.5*( f(a) + f(b) )
        h = (b-a)/n
        for i in range(1, n):
            integral += f(a + i*h)
        return h*integral

Now we’re not evaluating f twice at every interior point.

Estimating error

Suppose you’ve used the trapezoid rule once, then you decide to use it again with half as large a step size in order to compare the results. If the results are the same within your tolerance, then presumably you have your result. Someone could create a function where this comparison would be misleading, where the two results agree but both are way off. But this is unlikely to happen in practice. As Einstein said, God is subtle but he is not malicious.

If you cut your step size h in half, you double your number of integration points. So if you evaluated your integrand at n points the first time, you’ll evaluate it at 2n points the second time. But half of these points are duplicates. It would be more efficient to save the function evaluations from the first integration and reuse them in the second integration, only evaluating your function at the n new integration points.

It would be most efficient to write your code to directly save previous results, but using memoization would be easier and still more efficient than redundantly evaluating your integrand. We’ll illustrate this with Python code.

Now let’s integrate exp(cos(x)) over [0, π] with 4 and then 8 steps.

    from numpy import exp, cos, pi

    print( trapezoid2(f, 0, pi, 4) )
    print( trapezoid2(f, 0, pi, 8) )

This prints

    3.97746388
    3.97746326

So this suggests we’ve already found our integral to six decimal places. Why so fast? Because we’re integrating a periodic function. If we repeat our experiment with exp(x) we see that we don’t even get one decimal place agreement. The code

    print( trapezoid2(exp, 0, pi, 4 ) )
    print( trapezoid2(exp, 0, pi, 8 ) )

prints

    23.26
    22.42

Eliminating redundancy

The function trapezoid2 eliminated some redundancy, but we still have redundant function evaluations when we call this function twice as we do above. When we call trapezoid2 with n = 4, we do 5 function evaluations. When we call it again with n = 8 we do 9 function evaluations, 4 of which we’ve done before.

As we did in the Lobatto quadrature example, we will have our integrand function sleep for 10 seconds to make the function calls obvious, and we will add memoization to have Python to cache function evaluations for us.

    from time import sleep, time
    from functools import lru_cache

    @lru_cache()
    def f(x):
        sleep(10)
        return exp(cos(x))

    t0 = time()
    trapezoid2(f, 0, pi, 4)
    t1 = time()
    print(t1 - t0)
    trapezoid2(f, 0, pi, 8)
    t2 = time()
    print(t2 - t1)

This shows that the first integration takes 50 seconds and the second requires 40 seconds. The first integration requires 5 function evaluations and the second requires 9, but the latter is faster because it only requires 4 new function evaluations.

Romberg integration

In the examples above, we doubled the number of integration intervals and compared results in order to estimate our numerical integration error. A natural next step would be to double the number of intervals again. Maybe by comparing three integrations we can see a pattern and project what the error would be if we did more integrations.

Werner Romberg took this a step further. Rather than doing a few integrations and eye-balling the results, he formalized the inference using Richardson extrapolation to project where the integrations are going. Specifically, his method applies the trapezoid rule at 2^m points for increasing values of m. The method stops when either the maximum value of m has been reached or the difference between successive integral estimates is within tolerance. When Romberg’s method is appropriate, it converges very quickly and there is no need for m to be large.

To illustrate Romberg’s method, let’s go back to the example of integrating exp(x) over [0, π]. If we were to use the trapezoid rule repeatedly, we would get these results.

     Steps    Results
         1  37.920111
         2  26.516336
         4  23.267285
         8  22.424495
        16  22.211780
        32  22.158473

This doesn’t look promising. We don’t appear to have even the first decimal correct. But Romberg’s method applies Richardson extrapolation to the data above to produce a very accurate result.

    from scipy.integrate import romberg

    r = romberg(exp, 0, pi, divmax = 5) 
    print("exact:   ", exp(pi) - 1)
    print("romberg: ", r)

This produces

    exact:    22.1406926327792
    romberg:  22.1406926327867

showing that although none of the trapezoid rule estimates are good to more than 3 significant figures, the extrapolated estimate is good 12 figures, almost to 13 figures.

If you pass the argument show=True to romberg you can see the inner workings of the integration, including a report that the integrand was evaluated 33 times, i.e. 1 + 2^m times when m is given by divmax.

It seems mysterious how Richardson extrapolation could take the integral estimates above, good to three figures, and produce an estimate good to twelve figures. But if we plot the error in each estimate on a log scale it becomes more apparent what’s going on.

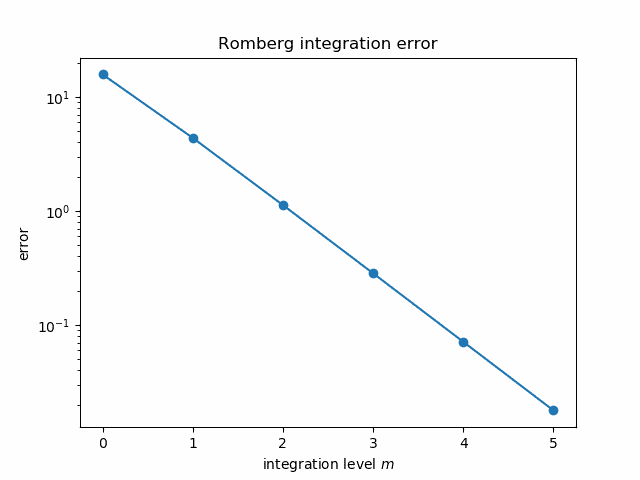
The errors follow nearly a straight line, and so the extrapolated error is “nearly” negative infinity. That is, since the log errors nearly follow a straight line going down, polynomial extrapolation produces a value whose log error is very large and negative.

More on numerical integration

• Scaling and Monte Carlo integration
• Lobatto integration
• Help with numerical integration

A basic idea in numerical integration is that if a method integrates polynomials exactly, it should do well on polynomial-like functions [1]. The higher the degree of polynomial it integrates exactly, the more accurate we expect it will be on functions that behave like polynomials.

The best known example of this is Gaussian quadrature. However, this post shows why for some applications you might want to use Lobatto quadrature instead. Lobatto quadrature is similar in spirit to Gaussian quadrature, but allocates points to solve a slightly different optimization problem.

Gaussian quadrature

If you need to integrate a function over an interval, it matters a great deal where you choose to evaluate the function. The optimal choice, in term of what polynomials you can integrate exactly, is to use Gaussian quadrature. By evaluating the integrand at n optimally chosen points you can integrate polynomials of degree 2n − 1 or less exactly.

So if Gaussian integration is optimal, why would you want to do anything else? The Gaussian integration points are all interior to the interval of integration. In some applications, you have to evaluate your integrand at the end points, and so you want to optimize subject to a constraint: how can you best allocate your integration points subject to the constraint that two of your integration points are the two ends of the interval? The solution is Lobatto quadrature, also called Gauss-Lobatto quadrature.

Lobatto quadrature

By evaluating the integrand at n points, two of which are the end points, Lobatto’s method exactly integrates polynomials of degree 2n-3.

Suppose for whatever reason you already know the value of the integrand evaluated at the end points. You’ve got m more function evaluations to spend. If you use those m points for Gaussian quadrature, you can exactly integrate polynomials of degree

2m − 1

or less. But if you use Lobatto quadrature, your m interior evaluations plus your two known values at the end points give you a total of m+2 function evaluations, and so can integrate polynomials of degree

2(m + 2) − 3 = 2m + 1

or less exactly, two degrees higher than if we had used Gaussian quadrature.

Next, suppose you only know the value of the function you’re integrating at one end point. Say you’ve already integrate f(x) over the interval [1, 2] using Lobatto quadrature, and now you want to integrate over [2, 3]. You already know the value f(2) from your previous integration.

Suppose you have m new function evaluations you can afford, and you don’t know f(3). If you use Lobatto quadrature, f(3) has to come out of your function evaluation budget, so you can afford m − 1 interior integration points. You then know the value of f(x) at m + 1 points: f(2) came for free, you evaluated f(x) at m − 1 interior points and at x = 3. This lets you exactly integrate polynomials of degree

2(m + 1) − 3 = 2m − 1

or less, the same as Gaussian quadrature. But if you then need to integrate over [3, 4], knowing f(3) gives you a head start on the next integration, and so on.

Weights and integration points

You can look up the weights and integration points for Gaussian quadrature and Lobatto quadrature in, for example, Abramowitz and Stegun.

There is a nice symmetry between the two integration methods: Gaussian quadrature uses integration points based on the zeros of Legendre polynomials, and weights that depend on the derivatives of these polynomials. Lobatto quadrature is the other way around: integration points are given by the zeros of derivatives of Legendre polynomials, and the weights involve the Legendre polynomials themselves.

Python example

Here we’ll implement the Gauss and Lobatto rules of order five. Most of the code is data on integration points and weights.

    gauss_points = [
        -0.906179845938664,
        -0.538469310105683,
        0.0,
        +0.538469310105683,
        +0.906179845938664
    ]
    
    gauss_weights = [
        0.23692688505618908,
        0.47862867049936647,
        0.5688888888888889,
        0.47862867049936647,    
        0.23692688505618908
    ]
    
    lobatto_points = [
        -1.0,
        -0.6546536707079771,
        0,
        +0.6546536707079771,
        +1.0
    ]
    
    lobatto_weights = [
        0.1,
        0.5444444444444444,
        0.7111111111111111,
        0.5444444444444444,
        0.1
    ]

The integration points and weights are symmetrical, so you could make the code more compact at the expense of making it a little more complicated. Putting the + in front of positive integration points is a little unconventional, but it emphasizes the symmetry by making the positive and negative weights align vertically.

Here’s our integration code:

    def integrate(f, xs, ws):
        return sum(f(xs[i])*ws[i] for i in range(5))

where we pass it the function to integrate and either Gauss data or Lobatto data.

The following verifies that with 5 integration points, Gauss should be able to exactly integrate a 9th order polynomial, and Lobatto should be able to integrate a 7th order polynomial.

    print( integrate(lambda x: x**9 + 1,
               gauss_points, gauss_weights) )

    print( integrate(lambda x: x**7 + 1,
               lobatto_points, lobatto_weights) )

Both print 2.0 as expected. The integral of an odd function over [−1, 1] is zero, and the integral of 1 over the same interval is 2.

Now let’s use both to integrate cosine over [−1, 1].

    print( integrate(cos, gauss_points, gauss_weights) )
    print( integrate(cos, lobatto_points, lobatto_weights) )

The exact integral is 2 sin(1). Here are the results.

    Exact:   1.682941969
    Gauss:   1.682941970
    Lobatto: 1.682942320

So Gauss is correct to 8, almost 9, decimal places, and Lobatto is correct to 5 decimal places.

Next, let’s hard code a 3rd order Gauss rule for comparison.

    def gauss3(f):
        k = 0.6**0.5
        s = f(-k)*5 + f(0)*8 + f(k)*5
        return s/9

We can verify that it integrates fifth order polynomials exactly:

    print(gauss3(lambda x: x**5 + 1))

and we can use it to integrate cosine:

    print(gauss3(cos))

This returns 1.68300, a little less accurate then the Lobatto rule above, illustrating that typically Lobatto will be more accurate than Gauss with the same number of function evaluations interior to the interval of integration.

More on numerical integration

• Orthogonal polynomials and Gaussian quadrature [pdf]
• Double exponential integration
• Numerically integrating periodic functions

[1] Polynomials can’t have horizontal asymptotes, for example, and so we should not be surprised that a method that integrates high order polynomials exactly could still do poorly on, say, a normal probability density.