The time-traveling professor

Posted on by John

Suppose you were a contemporary professor sent back in time. You need to continue your academic career, but you can’t let anyone know that you’re from the future. You can’t take anything material with you but you retain your memories.

At first thought you might think you could become a superstar, like the musician in the movie Yesterday who takes credit for songs by The Beatles. But on second thought, maybe not.

Maybe you’re a physicist and you go back in time before relativity. If you go back far enough, people will not be familiar with the problems that relativity solves, and your paper on relativity might not be accepted for publication. And you can’t just post it on arXiv.

If you know about technology that will be developed, but you don’t know how to get there using what’s available in the past, it might not do you much good. Someone with a better knowledge of the time’s technology might have the advantage.

If you’re a mathematician and you go back in time 50 years, could you scoop Andrew Wiles on the proof of Fermat’s Last Theorem? Almost certainly not. You have the slight advantage of knowing the theorem is true, whereas your colleagues only strongly suspect that it’s true. But what about the proof?

If I were in that position, I might think “There’s something about a Seaborn group? No, that’s the Python library. Selmer group? That sounds right, but maybe I’m confusing it with the musical instrument maker. What is this Selmer group anyway, and how does it let you prove FLT?”

Could Andrew Wiles himself reproduce the proof of FTL without access to anything written after 1971? Maybe, but I’m not sure.

In your area of specialization, you might be able to remember enough details of proven results to have a big advantage over your new peers. But your specialization might be in an area that hasn’t been invented yet, and you might know next to nothing about areas of research that are currently in vogue. Maybe you’re a whiz at homological algebra, but that might not be very useful in a time when everyone is publishing papers on differential equations and special functions.

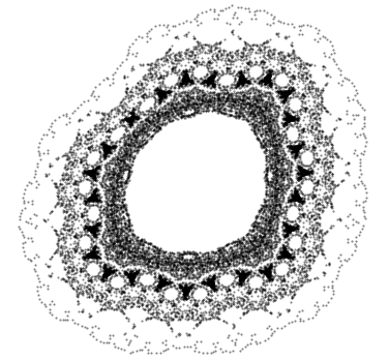
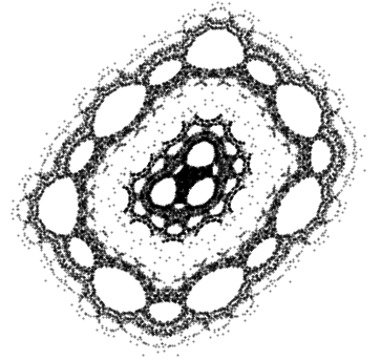
There are a few areas where a time traveler could make a big splash, areas that could easily have been developed much sooner but weren’t. For example, the idea of taking the output of a function and sticking it back in, over and over, is really simple. But nobody looked into it deeply until around 50 years ago.

Then came the Mandelbrot set, Feigenbaum’s constants, period three implies chaos, and all that. A lack of computer hardware would be frustrating, but not insurmountable. Because computers have shown you what phenomena to look for, you could go back and reproduce them by hand.

In most areas, I suspect knowledge of the future wouldn’t be an enormous advantage. It would obviously be some advantage. Knowing which way a conjecture was settled tells you whether to try to prove or disprove it. In the language of microprocessors, it gives you good branch prediction. And it would help to have patterns in your head that have turned out to be useful, even if you couldn’t directly appeal to these patterns without blowing your cover. But I suspect it might make you something like 50% more productive, not enough to turn an average researcher into a superstar.

The debauch of indices

Posted on by John

This morning I was working on a linear algebra problem for a client that I first solved by doing calculations with indices. As I was writing things up I thought of the phrase “the debauch of indices” that mathematicians sometimes use to describe tensor calculations. The idea is that calculations with lots of indices are inelegant and that more abstract arguments are better.

The term “debauch of indices” pejorative, but I’ve usually heard it used tongue-in-cheek. Although some people can be purists, going to great lengths to avoid index manipulation, pragmatic folk move up and down levels of abstraction as necessary to get their work done.

I searched on the term “debauch of indices” to find out who first said it, and found an answer on Stack Exchange that traces it back to Élie Cartan. Cartan said that although “le Calcul différentiel absolu du Ricci et Levi-Civita” (tensor calculus) is useful, “les débauches d’indices” could hide things that are easier to see geometrically.

After solving my problem using indices, I went back and came up with a more abstract solution. Both approaches were useful. The former cut through a complicated problem formulation and made things more tangible. The latter revealed some implicit pieces of the puzzle that needed to be made explicit.

Related posts

Not-to-do list

Posted on by John

There is an apocryphal [1] story that Warren Buffett once asked someone to list his top 25 goals in order. Buffett then told him that he should avoid items 6 through 25 at all costs. The idea is that worthy but low-priority goals distract from high-priority goals.

Paul Graham wrote something similar about fake work. Blatantly non-productive activity doesn’t dissipate your productive energy as unimportant work does.

I have a not-to-do list, though it’s not as rigorous as the “avoid at all costs” list that Buffett is said to have recommended. These are not hard constraints, but more like what optimization theory calls soft constraints, more like stiff springs than brick walls.

One of the things on my not-to-do list is work with students. They don’t have money, and they often want you to do their work for them, e.g. to write the statistical chapter of their dissertation. It’s easier to avoid ethical dilemmas and unpaid invoices by simply turning down such work. I haven’t made exceptions to this one.

My softest constraint is to avoid small projects, unless they’re interesting, likely to lead to larger projects, or wrap up quickly. I’ve made exceptions to this rule, some of which I regret. My definition of “small” has generally increased over time.

I like the variety of working on lots of small projects, but it becomes overwhelming to have too many open projects at the same time. Also, transaction costs and mental overhead are proportionally larger for small projects.

Most of my not-to-do items are not as firm as my prohibition against working with students but more firm than my prohibition against small projects. These are mostly things I have pursued far past the point of diminishing return. I would pick them back up if I had a reason, but I’ve decided not to invest any more time in them just-in-case.

Sometimes things move off my not-to-do list. For example, Perl was on my not-to-do list for a long time. There are many reasons not to use Perl, and I agree with all of them in context. But nothing beats Perl for small text-munging scripts for personal use.

I’m not advocating my personal not-to-do list, only the idea of having a not-to-do list. And I’d recommend seeing it like a storage facility rather than a landfill: some things may stay there a while then come out again.

I’m also not advocating evaluating everything in terms of profit. I do lots of things that don’t make money, but when I am making money, I want to make money. I might take on a small project pro bono, for example, that I wouldn’t take on for work. I heard someone say “Work for full rate or for free, but not for cheap” and I think that’s good advice.

***

[1] Some sources say this story may be apocryphal. But “apocryphal” means of doubtful origin, so it’s redundant to say something may be apocryphal. Apocryphal does not mean “false.” I’d say a story might be false, but I wouldn’t say it might be apocryphal.

Herd immunity countdown

Posted on by John

A few weeks ago I wrote a post giving a back-of-the-envelope calculation regarding when the US would reach herd immunity to SARS-COV-2. As I pointed out repeatedly, this is only a rough estimate because it makes numerous simplifying assumptions and is based on numbers that have a lot of uncertainty around them. See that post for details.

That post was based on the assumption that 26 million Americans had been infected with the virus. I’ve heard other estimates of 50 million or 100 million.

Update: The CDC estimates that 83 million Americans were infected in 2020 alone. I don’t see that they’ve issued any updates to this figure, but everyone who has been infected in 2021 brings us closer to herd immunity.

The post was also based on the assumption that we’re vaccinating 1.3 million per day. A more recent estimate is 1.8 million per day. (Update: We’re at 2.7 million per day as of March 30, 2021.) So maybe my estimate was pessimistic. On the other hand, the estimate for the number of people with pre-existing immunity that I used may have been optimistic.

Because there is so much we don’t know, and because numbers are frequently being updated, I’ve written a little Python code to make all the assumptions explicit and easy to update. According to this calculation, we’re 45 days from herd immunity. (Update: We could be at herd immunity any time now, depending on how many people had pre-existing immunity.)

As I pointed out before, herd immunity is not a magical cutoff with an agreed-upon definition. I’m using a definition that was suggested a year ago. Viruses never [1] completely go away, so any cutoff is arbitrary.

Here’s the code. It’s Python, but you it would be trivial to port to any programming language. Just remove the underscores as thousands separators if your language doesn’t support them and change the comment marker if necessary.

US_population         = 330_000_000
num_vaccinated        =  50_500_000 # As of March 30, 2021
num_infected          =  83_100_000 # As of January 1, 2021
vaccine_efficacy      = 0.9
herd_immunity_portion = 0.70

# Some portion of the population had immunity to SARS-COV-2
# before the pandemic. I've seen estimates from 10% up to 60%.
portion_pre_immune = 0.30
num_pre_immune = portion_pre_immune*US_population

# Adjust for vaccines given to people who are already immune.
portion_at_risk = 1.0 - (num_pre_immune + num_infected)/US_population

num_new_vaccine_immune = num_vaccinated*vaccine_efficacy*portion_at_risk

# Number immune at present
num_immune = num_pre_immune + num_infected + num_new_vaccine_immune
herd_immunity_target = herd_immunity_portion*US_population

num_needed = herd_immunity_target - num_immune

num_vaccines_per_day = 2_700_000 # As of March 30, 2021
num_new_immune_per_day = num_vaccines_per_day*portion_at_risk*vaccine_efficacy

days_to_herd_immunity = num_needed / num_new_immune_per_day

print(days_to_herd_immunity)

[1] One human virus has been eliminated. Smallpox was eradicated two centuries after the first modern vaccine.

Martin’s doileys

Posted on by John

An iteration due to artist mathematician [1] Barry Martin produces intricate doiley-like patterns by iterating a simple mathematical function. I ran across this via [2].

{x \choose y} \to {y - \text{sign}(x)\sqrt{bx -c|} \choose a - x} % pardon the non-semantic use of choose

The images produced are sensitive to small changes in the starting parameters x and y, as well as to the parameters a, b, and c.

Here are three examples:

make_plot(5, 5, 30.5, 2.5, 2.5,

make_plot(5, 6, 30, 3, 3,

make_plot(3, 4, 5, 6, 7,

And here’s the Python code that was used to make these plots.

    import matplotlib.pyplot as plt
    from numpy import sign, empty

    def make_plot(x, y, a, b, c, filename, N=20000):
        xs = empty(N)
        ys = empty(N)
        for n in range(N):
            x, y = y - sign(x)*abs(b*x - c)**0.5, a - x
            xs[n] = x
            ys[n] = y
        plt.scatter(xs, ys, c='k', marker='.', s = 1, alpha=0.5)
        plt.axes().set_aspect(1)
        plt.axis('off')
        plt.savefig(filename)
        plt.close()

    make_plot(5, 5, 30.5, 2.5, 2.5, "doiley1.png")
    make_plot(5, 6, 30, 3, 3, "doiley2.png")
    make_plot(3, 4, 5, 6, 7, "doiley3.png")

[1] Tom Crilly identified Martin as an artist in [2] and I repeated this error. Barry Martin informed me of the error in the comments below.

[2] Desert Island Theorems: My Magnificent Seven by Tony Crilly. The Mathematical Gazette, Mar., 2001, Vol. 85, No. 502 (Mar., 2001), pp. 2-12

Divisibility by any prime

Posted on by John

Here is a general approach to determining whether a number is divisible by a prime. I’ll start with a couple examples before I state the general rule. This method is documented in [1].

First example: Is 2759 divisible by 31?

Yes, because

\begin{align*} \begin{vmatrix} 275 & 9 \\ 3 & 1 \end{vmatrix} &= 248 \\ \begin{vmatrix} 24 & 8 \\ 3 & 1 \end{vmatrix} &= 0 \end{align*}

and 0 is divisible by 31.

Is 75273 divisible by 61? No, because

\begin{align*} \begin{vmatrix} 7527 & 3 \\ 6 & 1 \end{vmatrix} &= 7509 \\ \begin{vmatrix} 750 & 9\\ 6 & 1 \end{vmatrix} &= 696\\ \begin{vmatrix} 69 & 6\\ 6 & 1 \end{vmatrix} &= 33 \end{align*}

and 33 is not divisible by 61.

What in the world is going on?

Let p be an odd prime and n a number we want to test for divisibility by p. Write n as 10a + b where b is a single digit. Then there is a number k, depending on p, such that n is divisible by p if and only if

\begin{align*} \begin{vmatrix} a & b \\ k & 1 \end{vmatrix} \end{align*}

is divisible by p.

So how do we find k?

  • If p ends in 1, we can take k = ⌊p / 10⌋.
  • If p ends in 3, we can take k = ⌊7p / 10⌋.
  • If p ends in 7, we can take k = ⌊3p / 10⌋.
  • If p ends in 9, we can take k = ⌊9p / 10⌋.

Here ⌊x⌋ means the floor of x, the largest integer no greater than x. Divisibility by even primes and primes ending in 5 is left as an exercise for the reader. The rule takes more effort to carry out when k is larger, but this rule generally takes less time than long division by p.

One final example. Suppose we want to test divisibility by 37. Since 37*3 = 111, k = 11.

Let’s test whether 3293 is divisible by 37.

329 – 11×3 = 296

29 – 11×6 = -37

and so yes, 3293 is divisible by 37.

[1] R. A. Watson. Tests for Divisibility. The Mathematical Gazette, Vol. 87, No. 510 (Nov., 2003), pp. 493-494

Finding pi in pi with Perl

Posted on by John

Here’s a frivolous problem whose solution illustrates three features of Perl:

  1. Arbitrary precision floating point
  2. Lazy quantifiers in regular expressions
  3. Returning the positions of matched groups.

Our problem is to look for the digits 3, 1, 4, and 1 in the decimal part of π.

First, we get the first 100 digits of π after the decimal as a string. (It turns out 100 is enough, but if it weren’t we could try again with more digits.)

    use Math::BigFloat "bpi";

    $x = substr bpi(101)->bstr(), 2;

This loads Perl’s extended precision library Math::BigFloat, gets π to 101 significant figures, converts the result to a string, then lops off the first two characters “3.” at the beginning leaving “141592…”.

Next, we want to search our string for a 3, followed by some number of digits, followed by a 1, followed by some number of digits, followed by a 4, followed by some number of digits, and finally another 1.

A naive way to search the string would be to use the regex /3.*1.*4.*1/. But the star operator is greedy: it matches as much as possible. So the .* after the 3 would match as many characters as possible before backtracking to look for a 1. But we’d like to find the first 1 after a 3 etc.

The solution is simple: add a ? after each star to make the match lazy rather than greedy. So the regular expression we want is

   /3.*?1.*?4.*?1/

This will tell us whether our string contains the pattern we’re after, but we’d like to also know where the string contains the pattern. So we make each segment a captured group.

   /(3.*?)(1.*?)(4.*?)(1)/

Perl automatically populates an array @- with the positions of the matches, so it has the information we’re looking for. Element 0 of the array is the position of the entire match, so it is redundant with element 1. The advantage of this bit of redundancy is that the starting position of group $1 is in the element with index 1, the starting position of $2 is at index 2, etc.

We use the shift operator to remove the redundant first element of the array. Since shift modifies its argument, we can’t apply it directly to the constant array @-, so we apply it to a copy.

    if ($x =~ /(3.*?)(1.*?)(4.*?)(1)/) {
        @positions = @-;
        shift  @positions;
        print "@positions\n";
    }

This says that our pattern appears at positions 8, 36, 56, and 67. Note that these are array indices, and so they are zero-based. So if you count from 1, the first 3 appears in the 9th digit etc.

To verify that the digits at these indices are 3, 1, 4, and 1 respectively, we make the digits into an array, and slice the array by the positions found above.

    @digits = split(//, $x);
    print "@digits[@positions]\n";

This prints 3 1 4 1 as expected.

Solving for neck length

Posted on by John

A few days ago I wrote about my experiment with a wine bottle and a beer bottle. I blew across the empty bottles and measured the resulting pitch, then compared the result to the pitch you would get in theory if the bottle were a Helmholtz resonator. See the previous post for details.

Tonight I repeated my experiment with an empty water bottle. But I ran into a difficulty immediately: where would you say the neck ends?

water bottle

An ideal Helmholtz resonator is a cylinder on top of a larger sphere. My water bottle is basically a cone on top of a cylinder.

So instead of measuring the neck length L and seeing what pitch was predicted with the formula from the earlier post

f = \frac{v}{2\pi} \sqrt{\frac{A}{LV}}

I decided to solve for L and see what neck measurement would be consistent with the Helmholtz resonator approximation. The pitch f was 172 Hz, the neck of the bottle is one inch wide, and the volume is half a liter. This implies L is 10 cm, which is a little less than the height of the conical part of the bottle.

Trig functions across programming languages

Posted on by John

Programming languages are inconsistent in their support for trig functions, and inconsistent in the names they use for the functions they support. Several times I’ve been irritated by this and said that I should make a comparison chart someday, and today I finally did it.

Here’s the chart. The C column also stands for languages like Python that follow C’s conventions. More on this below.

\begin{tabular}{lllllll} \hline Mathematica & bc & C & NumPy & Perl & Math::Trig & CL\\ \hline Sin & s & sin & sin & sin & - & sin\\ Cos & c & cos & cos & cos & - & cos\\ Tan & - & tan & tan & - & tan & tan\\ Sec & - & - & - & - & sec & -\\ Csc & - & - & - & - & csc & -\\ Cot & - & - & - & - & cot & -\\ ArcSin & - & asin & arcsin & - & asin & asin\\ ArcCos & - & acos & arccos & - & acos & acos\\ ArcTan 1 arg & a & atan & arctan & - & atan & atan\\ ArcTan 2 arg & - & atan2 & arctan2 & atan2 & atan2 & atan\\ ArcSec & - & - & - & - & asec & -\\ ArcCsc & - & - & - & - & acsc & -\\ ArcCot & - & - & - & - & acot & -\\ \hline \end{tabular}

The table above is a PNG image. An HTML version of the same table is available here.

The rest of the post discusses details and patterns in the table.

Continue reading →

Da Vinci on wave propagation

Posted on by John

ocean waves

From Leonardo da Vinci:

The impetus is much quicker than the water, for it often happens that the wave flees the place of its creation, while the water does not; like the waves made in a field of grain by the wind, where we see the waves running across the field while the grain remains in place.

Quoted in Almost All About Waves by John R. Pierce