Dynamical systems

Calculating the period of Van der Pol oscillators

Posted on by John

A few days ago I wrote about how to solve differential equations with SciPy’s ivp_solve function using Van der Pol’s equation as the example. Van der Pol’s equation is

{d^2x \over dt^2}-\mu(1-x^2){dx \over dt}+x= 0

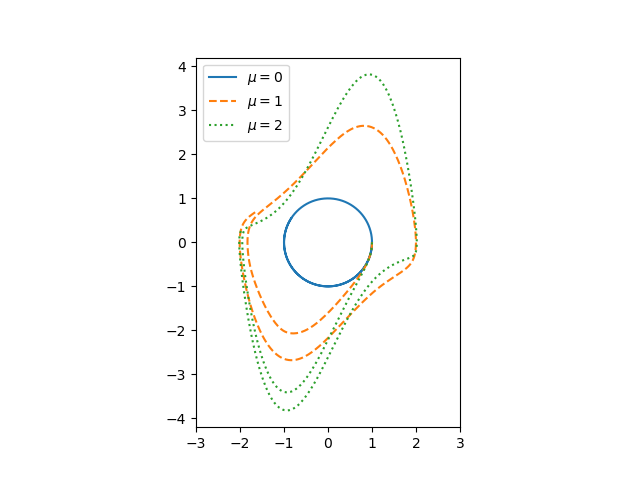
The parameter μ controls the amount of nonlinear damping. For any initial condition, the solution approach a periodic solution. The limiting periodic function does not depend on the initial condition [1] but does depend on μ. Here are the plots for μ  = 0, 1, and 2 from the previous post.

Van der Pol oscillator solutions as a function of time

A couple questions come to mind. First, how quickly do the solutions become periodic? Second, how does the period depend on μ? To address these questions, we’ll use an optional argument to ivp_solve we didn’t need in the earlier post.

Using events in ivp_solve

For ivp_solve an event is a function of the time t and the solution y whose roots the solver will report. To determine the period, we’ll look at where the solution is zero; our event function is trivial since we want to find the roots of the solution itself.

Recall from the earlier post that we cast our second order ODE as a pair of first order ODEs, and so our solution is a vector, the function x and its derivative. So to find roots of the solution, we look at what the solver sees as the first component of the solver. So here’s our event function:

    def root(t, y): return y[0]

Let’s set μ = 2 and find the zeros of the solution over the interval [0, 40], starting from the initial condition x(0) = 1, x‘(0) = 0.

    mu = 2
    sol = solve_ivp(vdp, [0, 40], [1, 0], events=root)
    zeros = sol.t_events[0]

Here we reuse the vdp function from the previous post about the Van der Pol oscillator.

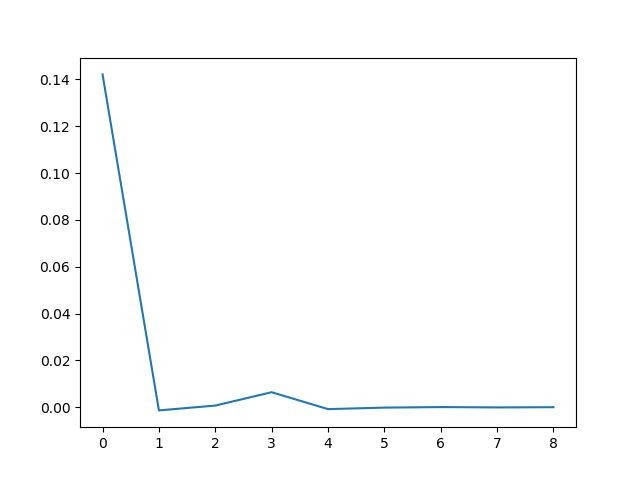
To estimate the period of the limit cycle we look at the spacing between zeros, and how that spacing is changing.

    spacing = zeros[1:] - zeros[:-1]
    deltas = spacing[1:] - spacing[:-1]

If we plot the deltas we see that the zero spacings quickly approach a constant value. Zero crossings are half periods, so the period of the limit cycle is twice the limiting spacing between zeros.

Van der pol period deltas

Theoretical results

If μ = 0 the Van der Pol oscillator reduces to a simple harmonic oscillator and the period is 2π. As μ increases, the period increases.

For relatively small μ we can calculate the period as above, but as μ increases this becomes more difficult numerically [2]. But one can easily show that the period is asymptotically

T ~ (3 – 2 log 2) μ

as μ goes to infinity. A more refined estimate due to Mary Cartwright is

T ~ (3 – 2 log 2) μ + 2π/μ1/3

for large μ.

More VdP posts

[1] There is a trivial solution, x = 0, corresponding to the initial conditions x(0) = x‘(0) = 0. Otherwise, every set of initial conditions leads to a solution that converges to the periodic attractor.

[2] To see why large values of μ are a problem numerically, here’s a plot of a solution for μ = 100.

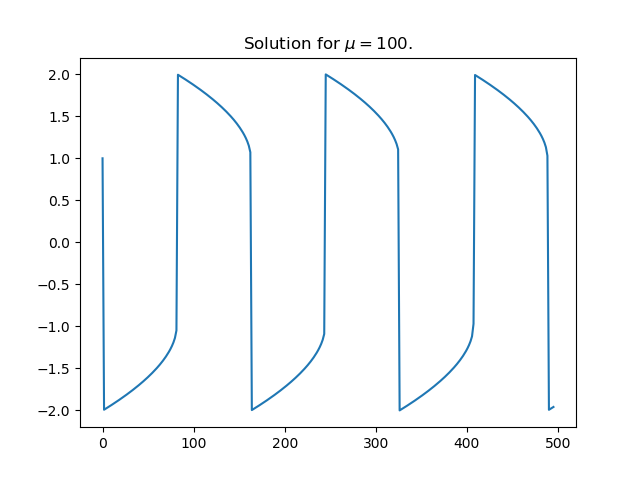
Solution to Van der Pol for large damping parameter mu

The solution is differentiable everywhere, but the derivative changes so abruptly at the maxima and minima that it is discontinuous for practical purposes.

Solving Van der Pol equation with ivp_solve

Posted on by John

Van der Pol’s differential equation is

{d^2x \over dt^2}-\mu(1-x^2){dx \over dt}+x= 0

The equation describes a system with nonlinear damping, the degree of nonlinearity given by μ. If μ = 0 the system is linear and undamped, but as μ increases the strength of the nonlinearity increases. We will plot the phase portrait for the solution to Van der Pol’s equation in Python using SciPy’s new ODE solver ivp_solve.

The function ivp_solve does not solve second-order systems of equations directly. It solves systems of first-order equations, but a second-order differential equation can be recast as a pair of first-order equations by introducing the first derivative as a new variable.

\begin{align*} {dx \over dt} &= y \\ {dy \over dt}&= \mu(1-x^2)y -x \\ \end{align*}

Since y is the derivative of x, the phase portrait is just the plot of (x, y).

Phase portait of Van der Pol oscillator

If μ = 0, we have a simple harmonic oscillator and the phase portrait is simply a circle. For larger values of μ the solutions enter limiting cycles, but the cycles are more complicated than just circles. These limiting cycles are periodic attractors: every non-trivial solution converges to the limit cycle.

Here’s the Python code that made the plot.

from scipy import linspace
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

def vdp(t, z):
    x, y = z
    return [y, mu*(1 - x**2)*y - x]

a, b = 0, 10

mus = [0, 1, 2]
styles = ["-", "--", ":"]
t = linspace(a, b, 500)

for mu, style in zip(mus, styles):
    sol = solve_ivp(vdp, [a, b], [1, 0], t_eval=t)
    plt.plot(sol.y[0], sol.y[1], style)
  
# make a little extra horizontal room for legend
plt.xlim([-3,3])    
plt.legend([f"$\mu={m}$" for m in mus])
plt.axes().set_aspect(1)

To plot the solutions as a function of time, rather than plotting phase portraits, change the line

    plt.plot(sol.y[0], sol.y[1], style)

to

    plt.plot(sol.t, sol.y[0], style)

and comment out the line setting xlim This gives the following plot.

Van der Pol oscillator solutions as a function of time

More dynamical system posts

The other butterfly effect

Posted on by John

monarch butterfly

The original butterfly effect

The butterfly effect is the semi-serious claim that a butterfly flapping its wings can cause a tornado half way around the world. It’s a poetic way of saying that some systems show sensitive dependence on initial conditions, that the slightest change now can make an enormous difference later. Often this comes up in the context of nonlinear, chaotic systems but it isn’t limited to that. I give an example here of a linear differential equation whose solutions start out the essentially the same but eventually diverge completely.

Once you think about these things for a while, you start to see nonlinearity and potential butterfly effects everywhere. There are tipping points everywhere waiting to be tipped!

The other butterfly effect

But a butterfly flapping its wings usually has no effect, even in sensitive or chaotic systems. You might even say especially in sensitive or chaotic systems.

Sensitive systems are not always and everywhere sensitive to everything. They are sensitive in particular ways under particular circumstances, and can otherwise be quite resistant to influence. Not only may a system be insensitive to butterflies, it may even be relatively insensitive to raging bulls. The raging bull may have little more long-term effect than a butterfly. This is what I’m calling the other butterfly effect.

Steering complex systems

In some ways chaotic systems are less sensitive to change than other systems. And this can be a good thing. Resistance to control also means resistance to unwanted tampering. Chaotic or stochastic systems can have a sort of self-healing property. They are more stable than more orderly systems, though in a different way.

The lesson that many people draw from their first exposure to complex systems is that there are high leverage points, if only you can find them and manipulate them. They want to insert a butterfly to at just the right time and place to bring about a desired outcome. Instead, we should humbly evaluate to what extent it is possible to steer complex systems at all. We should evaluate what aspects can be steered and how well they can be steered. The most effective intervention may not come from tweaking the inputs but from changing the structure of the system.

More dynamical systems posts

Duffing equation for nonlinear oscillator

Posted on by John

The Duffing equation is an ordinary differential equation describing a nonlinear damped driven oscillator.

\frac{d^2x}{dt} + h\frac{dx}{dt} + \Omega_0^2 x + \mu x^3 = F \cos \omega t

If the parameter μ were zero, this would be a damped driven linear oscillator. It’s the nonlinear x³ term that makes things nonlinear and interesting.

Using an analog computer in 1961, Youshisuke Ueda discovered that this system was chaotic. It was the first discovery of chaos in a second-order non-autonomous periodic system. Lorenz discovered his famous Lorenz attractor around the same time, though his system is third order.

Ueda’s system has been called “Ueda’s strange attractor” or the “Japanese attractor.”

In the linear case, when μ = 0, the phase portrait simply spirals outward from the origin towards its steady state.

But things get much more interesting when μ = 1. Here’s Mathematica code to numerically solve the differential equation and plot the phase portrait.

duff[t_] = 
    NDSolve[{x''[t] + 0.05 x'[t] + x[t] + x[t]^3 == 7.5 Cos[t], 
             x[0] == 0, x'[0] == 1}, x[t], {t, 0, 100}][[1, 1, 2]]
ParametricPlot[{duff[t], duff'[t]}, {t, 0, 50}, AspectRatio -> 1]

Here’s the same system integrated out further, to t = 200 rather 50.

Source: Wanda Szemplińska-Stupnicka. Chaos, Bifurcations and Fractals Around Us.

Iterating sines

Posted on by John

Pick a starting point x0 and define x1 = f(x0), x2 = f(x1), x3 = f(x2) etc. For which functions and which starting points does the sequence converge? If the sequence converges, how quickly does it converge? In general these are hard questions, but this post will answer a couple special cases.

If f(x) = sin(0.9x) and x0 = 0.5 + i, here’s what the iterations look like:

If the Taylor series for f(x) looks like a1x + a2x2 + a3x3 + … the iterates will converge if |a1| < 1 and your starting point is any complex number in a sufficiently small disk around the origin. The sequence might converge for starting points outside that disk, but there’s no guarantee.

The reason I chose sin(0.9x) for the example above rather than sin(x) is that the former has a1 = 0.9 and satisfies the theorem. The series for sin(x) has leading coefficient 1 and so the theorem doesn’t apply. For sin(x), the sequence of iterates does in fact converge starting at x0 = 0.5 + i but it diverges for other points, such as any purely imaginary starting point.

How fast do the iterates of f(x) converge if |a1| < 1? There is some constant b with |a1| < b < 1 such that | xn | < bn |x0 |. In other words, the sequence converges geometrically.

If we look at iterates of sin(x), the sequence converges for any starting value on the real line. The convergence is slower, on the order of 1/√n. And for points off the real line, the sequence may or may not converge.

Source: Asymptotic Methods in Analysis (Dover)

Update: See Mike Croucher’s blog post for a plot of the starting points where the sine iterates converge, repleat with Mathematica code.

See Mike's post for Mathematica code to make this plot