Privacy

Randomized response and local differential privacy

Posted on by John

Differential privacy protects user privacy by adding randomness as necessary to the results of queries to a database containing private data. Local differential privacy protects user privacy by adding randomness before the data is inserted to the database.

Using the visualization from this post, differential privacy takes the left and bottom (blue) path through the diagram below, whereas local differential privacy takes the top and right (green) path.

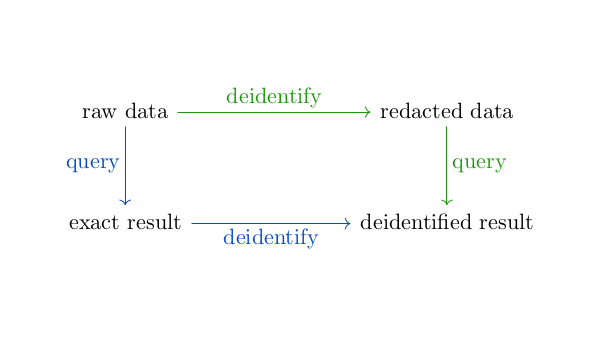
The diagram does not commute. Results are more accurate along the blue path. But this requires a trusted party to hold the identifiable data. Local differential privacy does not require trusting the recipient of the data to keep the data private and so the data must be deidentified before being uploaded. If you have enough data, e.g. telemetry data on millions of customers, then you can statistically afford to randomize your data before storing it.

I gave a simple description of randomized response here years ago. Randomized response gives users plausible deniability because their communicated responses are not deterministically related to their actual responses. That post looked at a randomized response to a simple yes/no question. More generally, you could have a question with k possible answers and randomize each answer to one of ℓ different possibilities. It is not necessary that k = ℓ.

A probability distribution is said to be ε-locally differentially private if for all possible pairs of inputs x and x′ and any output y, the ratio of the conditional probabilities of y given x and y given x′ is bounded by exp(ε). So when ε is small, the probability of any given output conditional on each possible input is roughly the same. Importantly, the conditional probabilities are not exactly the same, and so one can recover some information about the unrandomized response in aggregate via statistical means. However, it is not possible to infer any individual’s unrandomized response, assuming ε is small.

In the earlier post on randomized response, the randomization mechanism and the inference from the randomized responses were simple. With multiple possible responses, things are more complicated. You could choose different randomization mechanisms and different inference approaches for different contexts and priorities.

With local differential privacy, users can share their data without trusting the data recipient to keep the data private; in a real sense the recipient isn’t receiving personal data at all. The recipient is receiving the output of a stochastic process which is weakly correlated with individual data, but isn’t receiving individual data per se.

Local differential privacy scales up well, but it doesn’t scale down well. When ε is small, each data contributor has strong privacy protection, but the aggregate data isn’t very useful unless so many individuals are represented in the data that the randomness added to the responses can largely be statistically removed.

Related posts

PATE framework for differentially private machine learning

Posted on by John

Machine learning models can memorize fragments of their training data and return these fragments verbatim. I’ve seen instances, for example, where I believe an LLM returned phrases verbatim from this site. It’s easy to imagine how medical data might leak this way.

How might you prevent this? And how might you do it in a way that is easy to defend?

One such approach is the PATE framework. PATE stands for Private Aggregation of Teacher Ensembles. PATE was introduced in [1] and refined in [2].

In the PATE framework, you divide your sensitive data into n disjoint subsets and train a “teacher” model on each subset. These subsets are formed so that only one teacher has access to data from a particular individual.

Only these teacher models have direct access to sensitive data, and these models will not be released into production. Instead, the teacher models are used to train a “student” model.

The student model asks questions of the teacher models and so the student model is only indirectly trained on sensitive data. Furthermore, differential privacy is inserted between the student and teacher models as a further layer of privacy protection. So the student model is actually not trained on the answers from the teacher models but from an aggregate of the teacher models with a (ideally small) amount of randomness thrown in to further protect privacy. Publicly available data is also added to the training set for the student model.

There are a couple clever refinements in [2] that stretch the framework’s privacy budget.

To be more selective, our new mechanisms leverage some pleasant synergies between privacy and utility in PATE aggregation. For example, when teachers disagree, and there is no real consensus, the privacy cost is much higher; however, since such disagreement also suggest that the teachers may not give a correct answer, the answer may simply be omitted.

Differential privacy is a way of quantifying the notion that an individual’s participation or lack of participation in a database makes little difference. If the teacher models disagree, it may because an individual who is an outlier has had a large influence on the teacher model that was trained on his data. If you protect the privacy of the “teachers” then you protect the privacy of the individuals since no more than one teacher was training on any given individual’s data. When there is consensus among the teachers, there’s no need to spend much of the privacy budget.

The authors go on to say

Similarly, teachers may avoid giving an answer where the student already is confidently predicting the right answer.

Since each query uses some amount of the privacy budget, avoiding even asking questions saves budget.

Related posts

[1] Nicholas Papernot et al. Semi-supervised Knowledge Transfer for Deep Learning from Private Training Data arXiv:1610.05755

[2] Nicolas Papernot et al. Scalable Private Learning with PATE. arXiv:1802.08908v1

Earth mover’s distance

Posted on by John

There are many ways to describe the distance between two probability distributions. The previous two posts looked at using the p-norm to measure the difference between the PDFs and using Kullbach-Leibler divergence. Earth mover’s distance (EMD) is yet another approach.

Imagine a probability distribution on ℝ² as a pile of dirt. Earth mover’s distance measures how different two distributions are by how much work it would take to reshape the pile of dirt representing one distribution into a pile of dirt representing the other distribution. Unlike KL divergence, earth mover’s distance is symmetric, and so it really is a distance. (EMD is a colorful name for what is more formally known as the Wasserstein metric.)

The concept of t-closeness in data privacy is based on EMD. Deidentification procedures such as k-anonymity that protect individual privacy may not protect group privacy. t-closeness measures the distribution of values of some attribute in a group and compares this distribution to that of the overall distribution using EMD.

Earth mover’s distance is difficult to compute, or even to rigorously define, when working in several dimensions, but in one dimension it is particularly simple. The 1-Wasserman distance between two probability distributions is simply the 1-norm distance between the corresponding CDFs.

W_1(X, Y) = \int_{-\infty}^\infty |F_X(x) - F_Y(x)|\, dx
There are p-Wasserstein metrics just as there are p-norms, but the case p = 1 is particularly simple and so we will focus on it for this post.

We can illustrate the univariate Wasserstein metric by returning to a problem in a recent post, namely now to optimally approximate a standard normal by a logistic distribution.

Logistic distribution example

One of the nice things about the logistic distribution is that its CDF is an elementary function. If X is a logistic distribution with mean 0 and scale s then the CDF is

F_X(x) = \frac{1}{1 + \exp(-x/s)}

The CDF of a normal distribution has no elementary form but can be written in terms of the complementary error function. If Z is a standard normal random variable, then

F_Z(x) = \mbox{erfc}( -x/\sqrt{2}) / 2

We get a distance of 0.05926 if we use the value of s  = 0.5513 obtained from moment matching here. The optimal value is s = 0.5867, a little smaller than the optimal values of s when minimizing the 1, 2, and ∞ norms which were around 0.61.

Related posts

Differential entropy and privacy

Posted on by John

Differential entropy is the continuous analog of Shannon entropy. Given a random variable X with density function fX, the differential entropy of X, denoted h(X), is defined as

h(X) = -\int f_X(x) \log_2 f_X(x)\, dx

where the integration is over the support of fX. You may see differential entropy defined using logarithm to a different base, which changes h(X) by a constant amount.

In [1] the authors defined the privacy of a random variable X, denoted Π(X), as 2 raised to the power h(X).

\Pi(X) = 2^{h(X)}

This post will only look at “privacy” as defined above. Obviously the authors chose the name because of its application to privacy in the colloquial sense, but here we will just look at the mathematics.

Location and scale

It follows directly from the definitions above that location parameters do not effect privacy, and scale parameters change privacy linearly. That is, for σ > 0,

\Pi(\sigma X + \mu) = \sigma \,\Pi(X)

If we divide by standard deviation before (or after) computing privacy then we have a dimensionless quantity. Otherwise there’s more privacy is measuring a quantity in centimeters than in measuring it in inches, which is odd since both contain the same information.

Examples

If X is uniformly distributed on an interval of length a, then h(X) = log2 a and Π(X) = a.

The privacy of a standard normal random variable Z is √(2πe) and so the privacy of a normal random variable with mean μ and variance σ² is σ√(2πe).

The privacy of a standard exponential random variable is 1, so the privacy of an exponential with rate λ is 1/λ.

Bounds

A well-known theorem says that for given variance, differential entropy is maximized by a normal random variable. This means that the privacy of a random variable with variance σ² is bounded above by σ√(2πe).

The privacy of a Cauchy random variable with scale σ is 4πσ, which is greater than σ√(2πe). This does not contradict the statement above because the scaling parameter of a Cauchy random variable is not its standard deviation. A Cauchy random variable does not have and standard deviation.

Related posts

[1] Agrawal D., Aggrawal C. C. On the Design and Quantification of Privacy-Preserving Data Mining Algorithms, ACM PODS Conference, 2002. (Yes, the first author’s name contains one g and the second author’s name contains two.)

Identifiers depend on context

Posted on by John

Can you tell who someone is from their telephone number? That’s kinda the point of telephone numbers, to let you contact someone. And indeed telephone number is one the 18 identifiers under HIPAA Safe Harbor.

But whether any piece of information allows you to identify someone depends on context. If you don’t have access to a phone, or a phone book, or any electronic counterpart of a phone book, then a phone number doesn’t allow you to identify anyone. But once you can call a phone number or enter it into a search engine, then the phone number is identifiable. Maybe.

What if the number belongs to a burner phone? Then it would be harder to learn the identity of the person who owns the number, but not impossible. Maybe you couldn’t learn anything about the owner, but law enforcement officials could. Again identifiability depends on context.

An obvious identifier like a phone number might not be an identifier in some special circumstance. And an apparently useless bit of information might reveal someone’s identity in another circumstance.

HIPAA’s Safe Harbor Rule tries to say apart from context what kinds of data are identifiable. But if you read the Safe Harbor Rule carefully you’ll notice it isn’t so context-free as it seems. The last item in the list of 18 items to remove is “any other unique identifying number, characteristic, or code.” What might be an identifying characteristic? That depends on context.

The 19th rule of HIPAA Safe Harbor

Posted on by John

The HIPAA Safe Harbor provision says that data can be considered deidentified if 18 kinds of data are removed or reported at low resolution. At the end of the list of 18 items, there is an extra category, sometimes informally called the 19th rule:

The covered entity does not have actual knowledge that the information could be used alone or in combination with other information to identify an individual who is a subject of the information.

So if you otherwise meet the letter of the Safe Harbor provision, but you know (or should know) that the data can still be used to identify people represented in the data, then Safe Harbor does not apply.

The Department of Health and Human Services guidance document gives four examples of “when a covered entity would fail to meet the ‘actual knowledge’ provision.” The first concerns a medical record that would reveal someone’s identity by revealing their profession.

Revealing that someone is a plumber would probably not be a privacy risk, but in the HHS example someone’s occupation was listed as a former state university president. If you know what state this person is in, that greatly narrows down the list possibilities. One more detail, such as age, might be enough to uniquely identify this person.

Free text fields, such as physician notes, could easily contain this kind of information. Software that removes obvious names won’t catch this kind of privacy leak.

Not only are intentional free text fields a problem, so are unintentional free text fields. For example, a database field labeled CASENOTES is probably intended to contain free text. But other text fields, particularly if they are wider than necessary to contain the anticipated data, could contain identifiable information.

If you have data that does not fall under the Safe Harbor provision, or if you are not sure the Safe Harbor rules are enough to insure that the data are actually deidentified, let’s talk.

Related posts

This post is not legal advice. My clients are often lawyers, but I am not a lawyer.

Natural language processing and unnatural text

Posted on by John

I recently evaluated two software applications designed to find PII (personally identifiable information) in free text using natural language processing. Both failed badly, passing over obvious examples of PII. By contrast, I also tried natural language processing software on a nonsensical poem, it the software did quite well.

Doctor’s notes

It occurred to me later that the software packages to search for PII probably assume “natural language” has the form of fluent prose, not choppy notes by physicians. The notes that I tested did not consist of complete sentences marked up with grammatically correct punctuation. The text may have been transcribed from audio.

Some software packages deidentify medical notes better than others. I’ve seen some work well and some work poorly. I suspect the former were written specifically for their purpose and the latter were more generic.

Jabberwocky

I also tried NLP software on Lewis Carroll’s poem Jabberwocky. It too is unnatural language, but in a different sense.

Jabberwocky uses nonsense words that Carroll invented for the poem, but otherwise it is grammatically correct. The poem is standard English at the level of structure, though not at the level of words. It is the opposite of medical notes that are standard English at the word level (albeit with a high density of technical terms), but not at a structural level.

I used the spaCy natural language processing library on a couple stanzas from Lewis’ poem.

“Beware the Jabberwock, my son!
The jaws that bite, the claws that catch!
Beware the Jubjub bird, and shun
The frumious Bandersnatch!”

He took his vorpal sword in hand;
Long time the manxome foe he sought—
So rested he by the Tumtum tree
And stood awhile in thought.

I fed the lines into spaCy and asked it to diagram the lines, indicating parts of speech and dependencies. The software did a good job of inferring the use of even the nonsense words. I gave the software one line at a time rather than a stanza at a time because the latter results in diagrams that are awkwardly wide, too wide to display here. (The spaCy visualization software has a “compact” option, but this option does not make the visualizations much more compact.)

Here are the visualizations of the lines.








And here is the Python code I used to create the diagrams above.

    import spacy
    from spacy import displacy
    from pathlib import Path
    
    nlp = spacy.load("en_core_web_sm")
        
    lines = [
        "Beware the Jabberwock, my son!",
        "The jaws that bite, the claws that catch!",
        "Beware the Jubjub bird",
        "Shun the frumious Bandersnatch!",
        "He took his vorpal sword in hand.",
        "Long time the manxome foe he sought",
        "So rested he by the Tumtum tree",
        "And stood awhile in thought."
    ]
    
    for line in lines:
        doc = nlp(line)
        svg = displacy.render(doc, style="dep", jupyter=False)    
        file_name = '-'.join([w.text for w in doc if not w.is_punct]) + ".svg"
        output_path = Path(file_name)
        output_path.open("w", encoding="utf-8").write(svg)

Related posts

How an LLM might leak medical data

Posted on by John

Machine learning models occasionally memorize training data. Under the right prompt, a model could return portions of the training data verbatim.

If a large language model is trained on deidentified medical data, along with data that overlaps with the medical data, it could potentially leak details of a person’s medical history. I’m not saying that any particular LLM does leak data, but it’s something to watch out for if you are training an LLM.

One way to try to create a data leak would be to prompt the LLM with the data you have and see whether it will fill in more. For example, I asked Bing AI

Tell me about a man from Arkansas with ICD-10 code C50.921.

It came back with the following.

… Once upon a time, there was a man named John who lived in Arkansas. John was a hardworking man who loved spending time with his family and friends. One day, John noticed a lump in his right breast. He went to the doctor and was diagnosed with malignant neoplasm of unspecified site of the right male breast, classified under the ICD-10 code C50.921. …

I chose this diagnosis code because male breast cancer is extremely rare, and so the risk of reidentification is higher than for a more common diagnosis.

The model filled in the detail that the man’s name is John. This is not at all suspicious since John is the one of the most common male names in history. If the man’s name had been Vivek, there would be more cause to suspect the model is telling us about a real man name Vivek, though of course that could be a randomly chosen male name.

If a neural network were training on deidentified medical data, it could link fields together. If the story above had said “John, aged 42, …” the age might have been pulled from an actual patient record.

If the data the network was trained on was deidentified well, even leaking data verbatim should not create more than a very small risk of identification. However, if the data contained tokens linking the records to publicly available information, such as real estate records—this happens—then our hypothetical LLM might reveal more personal details that could be used to narrow down whose data is being leaked.

Related posts

Query, then deidentify

Posted on by John

Suppose you have a database of personally identifiable information (PII) and you want to allow someone else to query the data while protecting the privacy of the individuals represented by the data. There are two approaches:

  1. Deidentify, then query
  2. Query, then deidentify

The first approach is to do whatever is necessary to deidentify the data—remove some fields, truncate or randomize others, etc.—and then pose a query to this redacted data.

The second approach is to query the original data, then do whatever is necessary to deidentify the results.

In graphical terms, you can get from raw data to a deidentified result either by following the green arrows or the blue arrows below. In mathematical terms, this diagram does not commute.

The first approach is most common. A company that owns data (a “covered entity” in HIPAA terms) will deidentify it and license it to another company who then queries it. The second approach is becoming more common, where a company will license access to querying their data.

Pros and cons

Which approach is better? If by better you mean more accurate results, it’s always best to query first then deidentify. The order in which you do things matters, and deidentifying as late as possible preserves information.

The situation is analogous to carrying out a sequence of steps on a calculator. If you want your final result to be accurate to two decimal places, you first carry out all your operations to as much precision as you can, then round the final result. If you round your numbers first, you probably will get less accurate results, maybe even useless results.

However, deidentifying data before querying it is better in some non-mathematical ways. Data scientists want the convenience of working with the data with their tools in their environment. They want to possess (a deidentified version of) the data rather than have access to query the (exact) data. They also want the freedom to run ad hoc queries [1].

There are logistical and legal details to work out in order to license access to query data rather than licensing the data. But it is doable, and companies are doing it.

Why query first

When you deidentify data first, you have to guard against every possible use of the data. But when you deidentify data last, you only have to guard against the actual use of the data.

For example, suppose you are considering creating a new clinic and you would like to know how many patients of a certain type live closer to the location you have in mind than the nearest alternative. A data vendor cannot give you exact locations of patients. If they were to release such data, they’d have to obscure the addresses somehow, such as giving you the first three digits of zip codes rather than full addresses. But if you could ask your query of someone holding the full data, they may tell you exactly what you want to know.

Some queries may pose no privacy risk, and the data holder can return exact results. Or they may need to jitter the result a bit in order to protect privacy, for reasons explained here. But it’s better to jitter an exact result than to jitter your data before computing.

How to query first

The query-first approach requires a trusted party to hold the unredacted data. There are a variety of ways the data holder can license access, from simple to sophisticated, and in between.

The simplest approach would be for the data holder to sell reports. Maybe the data holder offers a predetermined set of reports, or maybe they allow requests.

The most sophisticated approach would be to use differential privacy. Clients are allowed to pose any query they wish, and a query manager automatically adds an amount of randomness to the results in proportion to the sensitivity of the query. All this is done automatically according to a mathematical model of privacy with no need for anyone to decide a priori which queries will be allowed.

There are approaches conceptually between pre-determined reports and differential privacy, offering more flexibility than the former and being easier to implement than the latter. There’s a lot of room for creativity in this space.

Related posts

[1] Being able to run ad hoc queries with no privacy budget is certainly simpler, in the same way that an all-you-can-eat buffet is simpler than ordering food à la carte. But it also means the price is higher. Deidentifying an entire data set entails more loss of accuracy that deidentifying a set of queries.

What can you learn from a credit card number?

Posted on by John

The first 4 to 6 digits of a credit card number are the bank identification number or BIN. The information needed to decode a BIN is publicly available, with some effort, and so anyone could tell from a credit card number what institution issued it, what bank it draws on, whether its a personal or business card, etc.

Suppose your credit card number was exposed in a data breach. Someone makes a suspicious purchase with your card, the issuer contacts you, you cancel the card, and you get a new card from the same source. The number can no longer be used to make purchases on your account, but what information did it leave behind?

The cancelled number might tell someone where you used to bank, which is probably where you still bank. And it may tell them the first few digits of your new card since the new card is issued by the same institution [1]. If the old BIN doesn’t directly reveal your new BIN, it at least narrows down the possibilities.

The information in your BIN, by itself, will not identify you, but it does provide clues that might lead to identifying you when combined with other information.

Related posts

[1] According to Andrew in the comments, American Express often changes credit card numbers as little as possible when issuing a replacement, changing only one content digit and the checksum.