Yesterday’s post looked at the distribution of powers of x mod 1. For almost all x > 1 the distribution is uniform in the limit. But there are exceptions, and the post raised the question of whether 3 + √2 is an exception.
A plot made it look like 3 + √2 is an exception, but that turned out to be a numerical problem.
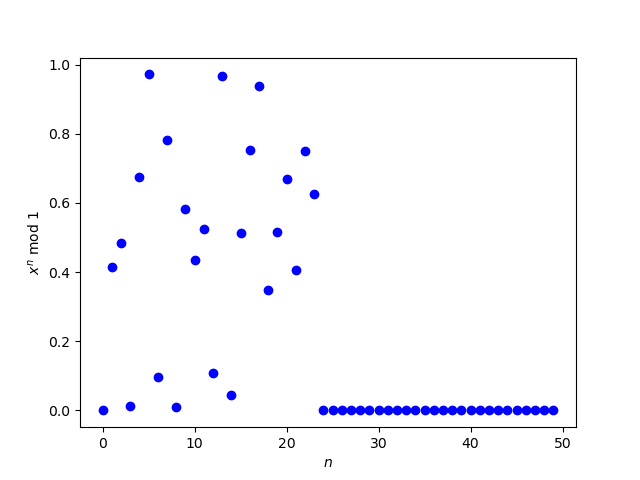
A higher precision calculation showed that the zeros on the right end of the plot were erroneous.
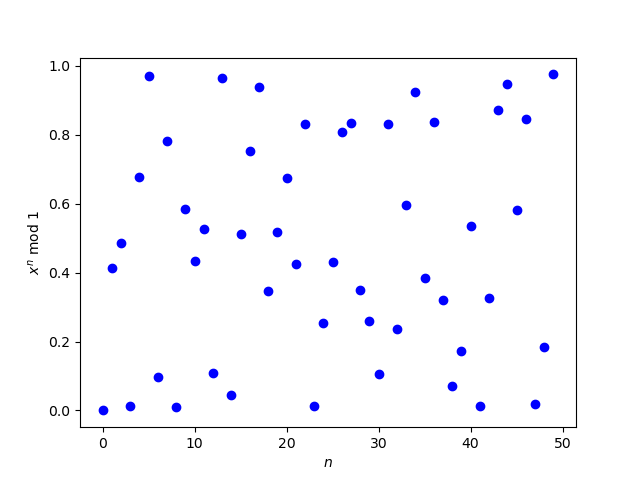
So this raises the question of how to calculate (3 + √2)n accurately for large n. The way I created the second plot was to use bc to numerically calculate the powers of 3 + √2. In this post, I’ll look at using Mathematica to calculate the powers symbolically.
For all positive integers n,
(3 + √2)n = an + bn√2
where an and bn are positive integers. We want to compute the a and b values.
If you ask Mathematica to compute (3 + √2)n it will simply echo the expression. But if you use the Expand function it will give you want you want. For example
Expand[(3 + Sqrt[2])^10]
returns
1404491 + 993054 √2
We can use the Coefficient function to split a + b √2 into a and b.
parts[n_] :=
Module[{x = (3 + Sqrt[2])^n},
{Coefficient[x, Sqrt[2], 0], Coefficient[x, Sqrt[2], 1]}]
Now parts[10] returns the pair {1404491, 993054}.
Here’s something interesting. If we set
(3 + √2)n = an + bn√2
as above, then the two halves of the expression on the right are asymptotically equal. That is, as n goes to infinity, the ratio
an / bn√2
converges to 1.
We can see this by defining
ratio[n_] :=
Module[ {a = Part[ parts[n], 1], b = Part[parts[n], 2]},
N[a / (b Sqrt[2])]]
and evaluating ratio at increasing values of n. ratio[12] returns 1.00001 and ratio[13] returns 1, not that the ratio is exactly 1, but it is as close to 1 as a floating point number can represent.
This seems to be true more generally, as we can investigate with the following function.
ratio2[p_, q_, r_, n_] :=
Module[{x = (p + q Sqrt[r])^n},
N[Coefficient[x, Sqrt[r], 0]/(Coefficient[x, Sqrt[r], 1] Sqrt[r])]]
When r is a prime and
(p + q√r)n = an + bn√r
then it seems that the ratio an / bn √r converges to 1 as n goes to infinity. For example, ratio2[3, 5, 11, 40] returns 1, meaning that the two halves of the expression for (3 + 5√11)n are asymptotically equal.
I don’t know whether the suggested result is true, or how to prove it if it is true. Feels like a result from algebraic number theory, which is not something I know much about.
Update: An anonymous person on X suggested a clever and simple proof. Observe that
In this form it’s clear that the ratio an / bn √2 converges to 1, and the proof can be generalized to cover more.