Science

Alien astronomers and Benford’s law

Posted on by John

alien astronomer image created by DALL-E

In 1881, astronomer Simon Newcomb noticed something curious. The first pages in books of logarithms were dirty on the edge, while the pages became progressively cleaner in later pages. He inferred from this that people more often looked up the logarithms of numbers with small leading digits than with large leading digits.

Why might this be? One might reasonably expect the numbers that came up in work to be uniformly distributed. But as often the case, it helps to ask “Uniform on what scale?”

Newcomb might have imagined his counterpart on another planet. This alien astronomer might have 12 fingers [1] and count in base 12. Base 10 is not inevitable, even for creatures with 10 fingers: the ancient Sumerians used a base-60 number system.

If Newcomb’s twelve-fingered counterpart had developed logarithms but not digital computers, he might have tables of duodecimal logarithms bound into books, and he too might noticed that pages with small leading (duo)digits are more frequently referenced. Both astronomers would naturally look up the logarithms of physical constants, physical distances, and so fort, numbers that vary over a practically unlimited range. The unlimited range is important.

On what scale could both astronomers see the leading digits uniformly distributed?

If Newcomb needed to look up the logarithms of numbers over a limited range, say from 1 to 106, each with equal probability, then the leading digits would be uniformly distributed. But our alien astronomer would have no special interest in the number 106. He might want to look at numbers between 1 and 126. The leading digits of numbers over this range would be uniformly distributed when represented in base 12, but not when represented in base 10. The choice of upper limit introduces a bias in one base or another.

Now suppose the numbers that both astronomers used in their work were uniformly distributed on a logarithmic scale. Newcomb conjectured that the numbers that came up in practice were uniformly distributed in their logarithms base 10. Our alien astronomer might conjecture the same thing for logarithms base 12. And both could be right. So would a third astronomer working in base 42. All logarithms are proportional, and so numbers uniformly distributed on a log scale using one base are uniformly distributed on a log scale using any other base.

Benford’s law says that the leading digits of numbers that come up in practice are uniformly distributed on a log scale. This applies to base 10, but also any other base, such as base 100. If you looked at the first two digits and thought of them as single base-100 digits, Benford’s law still applies.

But who is Benford? True to Stigler’s law of eponymy, Newcomb’s observation is named after physicist Frank Benford who independently made the same observation in 1938 and who tested it more extensively.

Let’s look at a set of physical constants and see how well Benford’s law applies. I took at list of physical constants from NIST and made a histogram of the leading digits to compare with what one would expect from Benford’s law.

If one were to write the NIST constants in base 12 and repeat the exercise, the result would look similar.

Related posts

[1] The image at the top of the post was created by DALL-E. There is a slight hint of an extra finger. DALL-E usually has a hard problem with hands, adding or removing fingers. But my attempts to force it to draw a hand with an extra finger were not successful.

Oval orbits?

Posted on by John

Johannes Kepler thought that planetary orbits were ellipses. Giovanni Cassini thought they were ovals. Kepler was right, but Cassini wasn’t far off.

In everyday speech, people use the words ellipse and oval interchangeably. But in mathematics these terms are distinct. There is one definition of an ellipse, and several definitions of an oval. To be precise, you have to say what kind of oval you have in mind, and in the context of this post by oval I will always mean a Cassini oval.

Ellipses and ovals each have two foci, f1 and f2. Let d1(p) and d2(p) be the distances from a point p to each of the foci. For an ellipse, the sum d1(p) + d2(p) is constant. For an oval, the product d1(p) d2(p) is constant.

In [1] the authors argue that just as planetary orbits are nearly circles, they’re also nearly ovals. This post will look at how far the earth’s orbit is from a circle and from an oval.

We need a way to specify which oval we want to compare to the ellipse of earth’s orbit. We’ll do this by equating the major and minor semi-axes of the two curves. These are usually denoted a and b, but the same variables have a different meaning in the context of ovals, so I’ll denote them by M for major and m for minor.

The equation of an ellipse is

(x/M)² + (y/m)² = 1

and the equation of an oval is

((x + a)² + y²) ((x – a)² + y²) = b².

Setting x = 0 in the equation of an oval tells us

m² = b – a²

and setting y = 0 tells us

M² = b + a².

So

b = (M² + m²)/2

and

a² = (M² – m²)/2.

For the earth’s orbit, M = 1.00000011 and m = 0.99986048 measured in AU, astronomical units. So or oval has parameters

a = 0.011816102

and

b = 0.99986060.

If you plot Kepler’s ellipse and Cassini’s oval for earth’s orbit at the same time, you can’t see the difference.

Planet orbits are nearly circular. If we compare a circle of radius 1 AU with Kepler’s ellipse we get a maximum error of about 1 part in 10,000.

But if we compare Cassini’s oval with Kepler’s ellipse we get a maximum error of about 1 part in 100,000,000.

 

In short, a circle is a good approximation to earth’s orbit, but a Cassini oval is four orders of magnitude better.

It would be difficult to empirically distinguish an ellipse from an oval as the shape of earth’s orbit, but theory is clearly on Kepler’s side since his ellipses fall out of Newton’s laws. Cassini’s error was more qualitative than quantitative.

More orbital mechanics posts

[1] Kepler’s ellipse, Cassini’s oval and the trajectory of planets. B Morgado1 and V Soares. 2014 Eur. J. Phys. 35 025009 DOI 10.1088/0143-0807/35/2/025009

Sphere of influence

Posted on by John

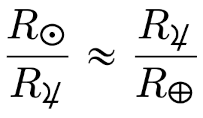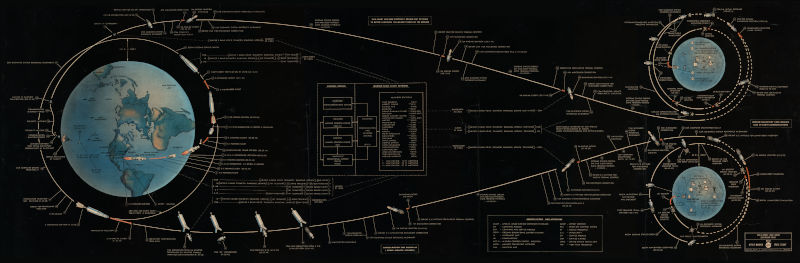
Apollo 11 orbit diagram via NASA

Suppose a spaceship is headed from the earth to the moon. At some point we say that the ship has left the earth’s sphere of influence is now in the moon’s sphere of influence (SOI). What does that mean exactly?

Wrong explanation #1

One way you’ll hear it described is that the moon’s sphere of influence is the point at which the earth is no longer pulling on the spaceship, but that’s nonsense. Everything has some pull on everything else, so how do you objectively say the earth’s pull is small enough that we’re now going to call it zero? And as we’ll see below, the earth’s pull is still significant even when the spaceship leaves earth’s SOI.

Wrong explanation #2

Another explanation you’ll hear is the moon’s sphere of influence is the point at which the moon is pulling on the spaceship harder than the earth is. That’s a better explanation, but still not right.

The distance from the earth to the moon is about 240,000 miles, and the radius of the moon’s SOI is about 40,000 miles. So when a spaceship first enters the moon’s SOI, it is five times closer to the moon than to the earth.

Newton’s law of gravity says gravitational force between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance. The mass of the earth is about 80 times that of the moon. So at the moon’s SOI boundary, the pull of the earth is 80/25 times as great as that of the moon, about three times greater.

Correct exlanation

So what does sphere of influence mean? The details are a little complicated, but essentially the moon’s sphere of influence is the point at which it’s more accurate to say the ship is orbiting the moon than to say it is orbiting the earth.

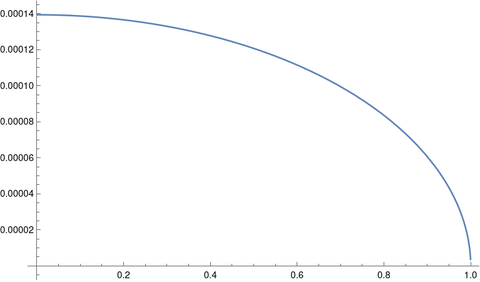
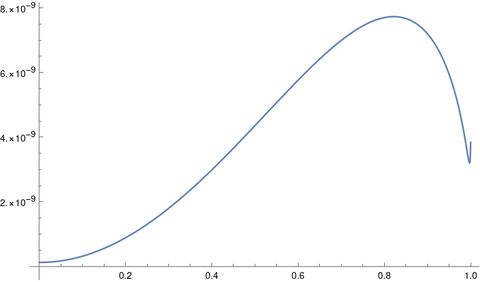
How can we say it’s better to think of the ship orbiting the moon than the earth when the earth is pulling on the ship three times as hard as the moon is? What matters is not so much the force of earth’s gravity as the effect of that force on the equations of motion.

The motion of an object between the earth and the moon could be viewed as an orbit around earth, with the moon exerting a perturbing influence, or as an orbit around the moon, with the earth exerting a perturbing influence.

At the boundary of the moon’s SOI the effect of the earth perturbing the ship’s orbit around the moon is equal to the effect of the moon perturbing its orbit around the earth. It’s a point at which it is convenient to switch perspectives. It’s not a physical boundary [1]. Also, the “sphere” of influence is not exactly a sphere but an approximately spherical region.

The moon has an effect on the ship’s motion when it’s on our side of the moon’s SOI, and the earth still has an effect on its motion after it has crossed into the moon’s SOI.

Calculating the SOI radius

As a rough approximation, the SOI boundary is where the ratio of the distances to the two bodies, e.g. moon and earth, equals the ratio of their masses to the exponent 2/5:

r/R = (m/M)2/5.

This approximation is better when the mass M is much larger than the mass m. For the earth and the moon, the equation is good enough for back-of-the-envelope equations but not accurate enough for planning a mission to the moon. Using the round numbers in this post, the left side of the equation is 1/5 = 0.2 and the right side is (1/80)0.4 = 0.17.

Context

Everything above has been in the context of the earth-moon system. Sphere of influence is defined relative to two bodies. When we spoke of a spaceship leaving the earth’s sphere of influence, we implicitly meant that it was leaving the earth’s sphere of influence relative to the moon.

Relative to the sun, the earth’s sphere of influence reaches roughly 600,000 miles. You could calculate this distance using the equation above. A spaceship like Artemis leaves the earth’s sphere of influence relative to the moon at some point, but never leaves the earth’s sphere of influence relative to the sun.

Related posts

[1] The sphere of influence sounds analogous to a continental divide, where rain falling on one side of the line ends up in one ocean and rain falling on the other side ends up in another ocean. But it’s not that way. I suppose you could devise an experiment to determine which side of the SOI you’re on, but it would not be a simple experiment. An object placed between the earth and the moon at the SOI boundary would fall to the earth unless it had sufficient momentum toward the moon.

The Pluto-Charon orbit

Posted on by John

The Moon doesn’t orbit the center of the Earth; it orbits the center of mass of the Earth-Moon system, which is inside the Earth. The distinction matters for designing satellite orbits, but it cannot be seen on a plot to scale. We’ll quantify this below.

Pluto’s moon Charon, however, is so large relative to Pluto and so close, that the center of mass of the Pluto-Charon system is outside of Pluto, and you can easily see this in a plot.

Plot of Pluto and Charon orbiting their barycenter

Imagine Pluto and Charon sitting on each end of a balanced seesaw. Pluto is a distance x1 to the left of the fulcrum, and Charon is a distance x2 to the right of the fulcrum. Let m1 be the mass of Pluto and m2 be the mass of Charon. Then

m1 x1 = m2 x2

and

x1 = m2 (x1 + x2) / (m1 + m2).

Now let’s put in some numbers.

m1 = 1.309 × 1022 kg
m2 = 1.62 × 1021 kg
x1 + x2 = 19,640 km

From this we find

x1 = (1.62 × 19640 / 14.71) km = 2163 km

and so the distance from the center of Pluto to the center of mass of the Pluto-Charon system is 2163 km. But the radius of Pluto is only 1190 km. So the center of mass of the Pluto-Charon system is about as far above the surface of Pluto as the center of Pluto is below the surface.

Comparison with the Earth-Moon system

It matters that the moon doesn’t exactly orbit the center of the Earth, but the difference between the center of the Earth and the center of mass of the Earth-Moon system is less dramatic. Let’s put in the numbers for the Earth and Moon.

m1 = 5.97 × 1024 kg
m2 = 7.346 × 1022 kg
x1 + x2 = 392,600 km

From this we find

x1 = (7.346 × 392,600 / 604) km = 4,775 km

The radius of Earth is 6,371 km, and so the center of mass of the Earth-Moon system is inside the Earth.

I made a plot analogous to the one above but for the Earth-Moon system. You could barely see the moon because it is so small relative to the size of its orbit. And you cannot see the difference between the center of the Earth and the barycenter of the Earth and Moon.

Tidal locking

Not only is Charon tidally locked with Pluto, as our moon is with Earth, but Pluto is tidally locked with Charon as well.

On Earth we only ever see one side of the moon. We never see the “dark side,” which is more accurately the “far side.” But someone standing on the moon would see Earth rotate.

Someone standing on Pluto would only ever see one side of Charon, and someone standing on Charon would only ever see one side of Pluto. Sputnik Planitia, the big heart-shaped feature on Pluto, is on the opposite side of Charon, so you could say Pluto is hiding its heart from its companion.

Image of Pluto featuring heart-shaped region

More orbital mechanics posts

Shape of moon orbit around sun

Posted on by John

The earth’s orbit around the sun is nearly a circle, and the moon’s orbit around the earth is nearly a circle, but what is the shape of the moon’s orbit around the sun?

You might expect it to be bumpy, bending inward when the moon is between the earth and the sun and bending output when the moon is on the opposite side of the earth from the sun. But in fact the shape of the moon’s orbit around the sun is convex as proved in [1] and illustrated below.

If the moon orbited the earth much faster, say 10 times faster, at the same altitude, then we see that the orbit is indeed bumpy.

However, the nothing could orbit the earth 10x faster than the moon at the same distance as the moon. Orbital period determines altitude and vice versa.

A more realistic example would be a satellite in MEO (Medium Earth Orbit) like a GPS satellite. Such a satellite orbits the earth roughly twice a day. The path of a MEO satellite around the sun is not convex.

The plot above shows about one day of an MEO satellite’s orbit around the sun. Note that the vertical and horizontal scales are not the same; it would be hard to see anything but a flat line if the scales were the same because the satellite is far closer to the earth than the sun.

Here are the equations from [1]. Choose units so that the distance to the moon or satellite is 1 and let d be the distance from the planet to the sun. Let p be the number of times the moon or satellite orbits the planet as the planet orbits the sun (the number of sidereal periods).

x(θ) = d cos(θ) + cos(pθ)
y(θ) = d sin(θ) + sin(pθ)

This assumes both the planet’s orbit around the sun and the satellite’s orbit around the planet are circular, which is a good approximation in our examples.

[1] Noah Samuel Brannen. The Sun, the Moon, and Convexity. The College Mathematics Journal, Vol. 32, No. 4 (Sep., 2001), pp. 268-272

Can Brownian motion do work?

Posted on by John

According to the latest episode of Eclectic Tech, Richard Feynman argued that Brownian motion cannot do work, but researchers at the University of Arkansas have demonstrated that it can by generating an electric current from Brownian motion in a sheet of graphene. You can read more in the physics journal article by the researchers.

Unfortunately this will be the last episode of Eclectic Tech. This last episode had several interesting stories. In addition to the story above, the episode discussed synchronizing clocks by observing cosmic ray events, a new bioinspired metamaterial, and NASA’s Inspire project.

More on Brownian motion

Infinite periodic table

Posted on by John

All the chemical elements discovered or created so far follow a regular pattern in how their electrons are arranged: the nth shell contains up to 2n – 1 suborbitals that each contain up to two electrons. For a given atomic number, you can determine how its electrons are distributed into shells and suborbitals using the Aufbau principle.

The Aufbau principle is a good approximation, but not exact. For this post we’ll assume it is exact, and that everything in the preceding paragraph generalizes to an arbitrary number of shells and electrons.

Under those assumptions, what would the periodic table look like if more elements are discovered or created?

D. Weiss worked out the recurrence relations that the periods of the table satisfy and found their solutions.

The number of elements in nth period works out to

P_n = \frac{(-1)^n(2n+3) + 2n^2 + 6n + 5}{4}

and the atomic numbers of the elements at the end of the nth period (the noble gases) are

Z_n = \frac{(-1)^n(3n+6) + 2n^3 + 12n^2 + 25n - 6}{12}

We can verify that these formulas give the right values for the actual periodic table as follows.

    >>> def p(n): return ((-1)**n*(2*n+3) + 2*n*n + 6*n +5)/4
    >>> def z(n): return ((-1)**n*(3*n+6) + 2*n**3 + 12*n**2 + 25*n - 6)/12
    >>> [p(n) for n in range(1, 8)]
    [2.0, 8.0, 8.0, 18.0, 18.0, 32.0, 32.0]
    >>> [z(n) for n in range(1, 8)]
    [2.0, 10.0, 18.0, 36.0, 54.0, 86.0, 118.0]

So, hypothetically, if there were an 8th row to the periodic table, it would contain 50 elements, and the last element of this row would have atomic number 168.

Related

Chemical element abbreviation patterns

Posted on by John

I’ve wondered occasionally about the patterns in how chemical elements are abbreviated. If you don’t know the abbreviation for an element, is there a simple algorithm that would let you narrow the range of possibilities or improve your odds at guessing?

Here’s a survey of how the elements are abbreviated.

Latin and German

The elements that have been known the longest often have abbreviations that are mnemonic in Latin.

  • Iron (Fe)
  • Sodium (Na)
  • Silver (Ag)
  • Tin (Sn)
  • Antimony (Sb)
  • Tungsten (W)
  • Gold (Au)
  • Mercury (Hg)
  • Lead (Pb)
  • Potassium (K)
  • Copper (Cu)

I included Tungsten in this section because it also has an abbreviation that is mnemonic in another language, in this case German.

Initial letter

The easiest abbreviations to remember are simply the first letters of the element names (in English).

  • Boron (B)
  • Carbon (C)
  • Fluorine (F)
  • Hydrogen (H)
  • Iodine (I)
  • Nitrogen (N)
  • Oxygen (O)
  • Phosphorus (P)
  • Sulfur (S)
  • Uranium (U)
  • Vanadium (V)
  • Yttrium (Y)

First two letters

The largest group of elements are those abbreviated by the first two letters of their name. When in doubt, guess the first two letters.

  • Actinium (Ac)
  • Aluminum (Al)
  • Americium (Am)
  • Argon (Ar)
  • Barium (Ba)
  • Beryllium (Be)
  • Bismuth (Bi)
  • Bromine (Br)
  • Calcium (Ca)
  • Cerium (Ce)
  • Chlorine (Cl)
  • Cobalt (Co)
  • Dysprosium (Dy)
  • Erbium (Er)
  • Europium (Eu)
  • Flerovium (Fl)
  • Francium (Fr)
  • Gallium (Ga)
  • Germanium (Ge)
  • Helium (He)
  • Holmium (Ho)
  • Indium (In)
  • Iridium (Ir)
  • Krypton (Kr)
  • Lanthanum (La)
  • Lithium (Li)
  • Lutetium (Lu)
  • Molybdenum (Mo)
  • Neon (Ne)
  • Nickel (Ni)
  • Nobelium (No)
  • Oganesson (Og)
  • Osmium (Os)
  • Polonium (Po)
  • Praseodymium (Pr)
  • Radium (Ra)
  • Rhodium (Rh)
  • Ruthenium (Ru)
  • Scandium (Sc)
  • Selenium (Se)
  • Silicon (Si)
  • Tantalum (Ta)
  • Tellurium (Te)
  • Thorium (Th)
  • Titanium (Ti)
  • Xenon (Xe)

Many of these elements use the first two letters to avoid a conflict with the first letter. For example, helium uses He because hydrogen already took H.

There are several elements that start with the same letter, and no element uses just the first letter. For example: actinium, aluminum, americium, and argon.

Xenon could have been X, or dysprosium could have been just D, but that’s not how it was done.

First letter and next consonant

The next largest group of elements are abbreviated by their first letter and the next consonant, skipping over a vowel.

  • Bohrium (Bh)
  • Cadmium (Cd)
  • Cesium (Cs)
  • Dubnium (Db)
  • Gadolinium (Gd)
  • Hafnium (Hf)
  • Hassium (Hs)
  • Livermorium (Lv)
  • Magnesium (Mg)
  • Manganese (Mn)
  • Meitnerium (Mt)
  • Neodymium (Nd)
  • Neptunium (Np)
  • Nihonium (Nh)
  • Niobium (Nb)
  • Rubidium (Rb)
  • Samarium (Sm)
  • Technetium (Tc)
  • Zinc (Zn)
  • Zirconium (Zr)

Many of these elements would cause a conflict if they had been abbreviated using one of the above rules. For example, cadmium could not be C because that’s carbon, and it could not be Ca because that’s calcium.

Initials of first two syllables

  • Astatine (At)
  • Berkelium (Bk)
  • Darmstadtium (Ds)
  • Einsteinium (Es)
  • Fermium (Fm)
  • Lawrencium (Lr)
  • Mendelevium (Md)
  • Moscovium (Mc)
  • Platinum (Pt)
  • Promethium (Pm)
  • Roentgenium (Rg)
  • Terbium (Tb)
  • Thallium (Tl)

Initials of first and third syllable

  • Californium (Cf)
  • Copernicium (Cn)
  • Palladium (Pd)
  • Rutherfordium (Rf)
  • Seaborgium (Sg)
  • Tennessine (Ts)
  • Ytterbium (Yb)

First and last letter

  • Curium (Cm)
  • Radon (Rn)
  • Thulium (Tm)

Miscellaneous

  • Arsenic (As)
  • Chromium (Cr)
  • Plutonium (Pu)
  • Protactinium (Pa)
  • Rhenium (Re)
  • Strontium (Sr)

Table

Update: Here’s a visualization of the categories above.

Periodic table of element abbreviations

Key to the groups above:

  1. First letter
  2. First two letters
  3. First letter and next consonant
  4. Initials of first and second syllables
  5. Initials of first and third syllables
  6. First and last letter
  7. First letter and something else
  8. Historical

Related posts

Oscillations in RLC circuits

Posted on by John

Electrical and mechanical oscillations satisfy analogous equations. This is the basis of using the word “analog” in electronics. You could study a mechanical system by building an analogous circuit and measuring that circuit in a lab.

Mass, dashpot, spring

Years ago I wrote a series of four posts about mechanical vibrations:

Everything in these posts maps over to electrical vibrations with a change of notation.

That series looked at the differential equation

m u'' + \gamma u' + k u = F \cos\omega t

where m is mass, γ is damping from a dashpot, and k is the stiffness of a spring.

Inductor, resistor, capacitor

Now we replace our mass, dashpot, and spring with an inductor, resistor, and capacitor.

Imagine a circuit with an L henry inductor, and R ohm resistor, and a C farad capacitor in series. Let Q(t) be the charge in coulombs over time and let E(t) be an applied voltage, i.e. an AC power source.

Charge formulation

One can use Kirchhoff’s law to derive

Here we have the correspondences

\begin{align*} u &\leftrightarrow Q \\ m &\leftrightarrow L \\ \gamma &\leftrightarrow R \\ k &\leftrightarrow 1/C \end{align*}

So charge is analogous to position, inductance is analogous to mass, resistance is analogous to damping, and capacitance is analogous to the reciprocal of stiffness.

The reciprocal of capacitance is called elastance, so we can say elastance is proportional to stiffness.

Current formulation

It’s more common to see the differential equation above written in terms of current I.

I = \frac{dQ}{dt}

If we take the derivative of both sides of

we get

LI'' + RI' + \frac{1}{C} I = E'

Natural frequency

With mechanical vibrations, as shown here, the natural frequency is

\omega_0 = \sqrt{\frac{k}{m}}

and with electrical oscillations this becomes

\omega_0 = \frac{1}{\sqrt{LC}}

Steady state

When a mechanical or electrical system is driven by sinusoidal forcing function, the system eventually settles down to a solution that is proportional to a phase shift of the driving function.

To be more explicit, the solution to the differential equation

m u'' + \gamma u' + k u = F \cos\omega t

has a transient component that decays exponentially and a steady state component proportional to cos(ωt-φ). The same is true of the equation

LI'' + RI' + \frac{1}{C} I = E'

The proportionality constant is conventionally denoted 1/Δ and so the steady state solution is

\frac{F}{\Delta} \cos(\omega t - \phi)

for the mechanical case and

\frac{T}{\Delta} \cos(\omega t - \phi)

for the electrical case.

The constant Δ satisfies

\Delta^2 = m^2(\omega_0^2 -\omega^2)^2 + \gamma^2 \omega^2

for the mechanical system and

\Delta^2 = L^2(\omega_0^2 -\omega^2)^2 + R^2 \omega^2

for the electrical system.

When the damping force γ or the resistance R is small, then the maximum amplitude occurs when the driving frequency ω is near the natural frequency ω0.

More on damped, driven oscillations here.

How is portable AM radio possible?

Posted on by John

The length of antenna you need to receive a radio signal is proportional to the signal’s wavelength, typically 1/2 or 1/4 of the wavelength. Cell phones operate at gigahertz frequencies, and so the antennas are small enough to hide inside the phone.

But AM radio stations operate at much lower frequencies. For example, there’s a local station, KPRC, that broadcasts at 950 kHz, roughly one megahertz. That means the wavelength of their carrier is around 300 meters. An antenna as long as a quarter of a wavelength would be roughly as long as a football field, and yet people listen to AM on portable radios. How is that possible?

looking inside a portable radio

There are two things going on. First, transmitting is very different than receiving in terms of power, and hence in terms of the need for efficiency. People are not transmitting AM signals from portable radios.

Second, the electrical length of an antenna can be longer than its physical length, i.e. an antenna can function as if it were longer than it actually is. When you tune into a radio station, you’re not physically making your antenna longer or shorter, but you’re adjusting electronic components that make it behave as if you were making it longer or shorter. In the case of an AM radio, the electrical length is orders of magnitude more than the physical length. Electrical length and physical length are closer together for transmitting antennas.

Here’s what a friend of mine, Rick Troth, said when I asked him about AM antennas.

If you pop open the case of a portable AM radio, you’ll see a “loop stick”. That’s the AM antenna. (FM broadcast on most portables uses a telescoping antenna.) The loop is tuned by two things: a ferrite core and the tuning capacitor. The core makes the coiled wiring of the antenna resonate close to AM broadcast frequencies. The “multi gang” variable capacitor coupled with the coil forms an LC circuit, for finer tuning. (Other capacitors in the “gang” tune other parts of the radio.) The loop is small, but is tuned for frequencies from 530KHz to 1.7MHz.

Loops are not new. When I was a kid, I took apart so many radios. Most of the older (tube type, and AM only) radios had a loop inside the back panel. Quite different from the loop stick, but similar electrical properties.

Car antennas don’t match the wavelengths for AM broadcast. Never have. That’s a case where matching matters less for receivers. (Probably matters more for satellite frequencies because they’re so weak.) Car antennas, whether whip from decades ago or embedded in the glass, probably match FM broadcast. (About 28 inches per side of a dipole, or a 28 inch quarter wave vertical.) But again, it does matter a little less for receive than for transmit.

In the photo above, courtesy Rick, the AM antenna is the copper coil on the far right. The telescoping antenna outside the case extends to be much longer physically than the AM antenna, even though AM radio waves are two orders of magnitude longer than FM radio waves.