Author: John

Minimize squared relative error

Posted on by John

Suppose you have a list of positive data points y1, y2, …, yn and you wanted to find a value α that minimizes the squared distances to each of the y‘s.

\sum_{i=1}^n (y_i - \alpha)^2

Then the solution is to take α to be the mean of the y‘s:

\alpha = \frac{1}{n} \sum_{i=1}^n y_i

This result is well known [1]. The following variation is not well known.

Suppose now that you want to choose α to minimize the squared relative distances to each of the y‘s. That is, you want to minimize the following.

\sum_{i=1}^n \left( \frac{y_i - \alpha}{\alpha} \right)^2

The value of alpha this expression is the contraharmonic mean of the y‘s [2].

\alpha = \frac{\sum_{i=1}^n y_i^2}{\sum_{i=1}^n y_i}

Related posts

[1] Aristotle says in the Nichomachean Ethics “The mean is in a sense an extreme.” This is literally true: the mean minimizes the sum of the squared errors.

[2] E. F. Beckenbach. A Class of Mean Value Functions. The American Mathematical Monthly. Vol. 57, No. 1 (Jan., 1950), pp. 1–6

What is the Bitcoin proof-of-work problem?

Posted on by John

In order to prevent fraud, anyone wanting to add a block to the Bitcoin blockchain must prove that they’ve put in a certain amount of computational work. This post will focus on what problem must be solved in order produce proof of work.

You’ll see the proof of work function described as finding strings whose SHA256 hash value begins with a specified number of 0s. That’s sort of a zeroth-level approximation of the problem.

The string s you’re trying to find has the form data + nonce where the data comes from the block you’re wanting to add and the nonce is a value you concatenate on the end. You try different values until you get an acceptable hash value.

You’re not computing the SHA256(s) but rather the double hash:

SHA256²(s) = SHA256( (SHA256(s) )

The only way to find such a string s is by brute force [1], and applying the hash function twice doubles the amount of brute force work needed.

And you’re not exactly trying to produce leading zeros; you’re trying to produce a value less than a target T. This is roughly the same thing, but not quite.

To illustrate this, suppose you have a 2FA fob that generates six-digit random numbers. You’ve been asked to wait until your fob generates a number less than 2025. Waiting until you have three leading zeros would be sufficient, but that would be making the task harder than it needs to be. You’d be waiting for a number less than 1000 when you’re only asked to wait for a number less than 2025.

A SHA256 hash value is a 256-bit number. If your target T is a power of 2

T = 2256−n

then finding a value of s such that

SHA256²(s) < T

really is finding an s whose (double) hash begins with n zeros, though T is not required to be a power of 2.

Finding a value of s with

SHA256²(s) < 2256−n

will require, on average, testing 2n values of s.

The value of T is adjusted over time in order to keep the amount of necessary work roughly constant. As miners have become more efficient, the value of T has gone down and the amount of work has gone up. But the value of T can go up as well. It is currently fluctuating around 2176, i.e. hashes must have around 80 leading zero bits.

Now here’s where things get a little more complicated. I said at the beginning that the string s has the form

s = data + nonce

where the data comes from the block you’re trying to add and the nonce is a number you twiddle in order to get the desired hash value. But the nonce is a 32-bit integer. If you need to hash on the order of 280 strings in order to find one with 80 leading zeros, you can’t do that just by adjusting a 32-bit nonce.

In practice you’re going to have to twiddle the contents of what I’ve called data. The data contains a Merkle tree of transactions, and you can change the hash values by adjusting the order in which transactions are arranged in the tree, in addition to adjusting the nonce.

Related posts

[1] Unless someone finds a flaw in SHA256, which cryptographers have been trying to do for years and have not been able to do. And if a significant weakness is found in SHA256, it may not translate into a significant flaw in SHA256².

Deleting vs Replacing Names

Posted on by John

This post looks at whether you should delete names or replace names when deidentifying personal data. With structured data, generating synthetic names does not increase or decrease privacy. But with unstructured data, replacing real names with randomly generated names increases privacy protection.

Structured data

If you want to deidentify structured data (i.e. data separated into columns in a database) then an obvious first step is to remove a column containing names. This is not sufficient—the reason deidentification is subtle is that it is possible to identify people after the obvious identifiers have been removed—but clearly removing names is necessary.

Instead of removing the names, you could replace them with randomly generated names. This neither hurts nor helps privacy. But this might be useful, say, when creating test data.

Say you’re developing software that handles patient data. You want to use real patient data because you want the test data to be realistic, but that may not be acceptable (or legal) due to privacy risks. You can’t just remove names because you need to test whether software displays names correctly, so you replace real names with randomly generated names. No harm, no foul.

Unstructured data

Now let’s switch contexts and look at unstructured data, such as text transcriptions of doctors’ notes. You still need to remove names, but it’s not as simple as removing the name column. Instead of the database structure telling you what’s a name, what’s a diagnosis, etc. you have to infer these things statistically [1], which means there will always be errors [2].

When working with unstructured text, replacing names with randomly generated names is better for privacy. If you could identify names with 100% accuracy, then it would make no difference whether you removed or replaced names, but you can’t. Software will always miss some names [3].

Suppose your software replaces suspected names with “NAME REDACTED.” When your software fails to identify a name, it’s obvious that it failed. For example,

NAME REDACTED and his wife Margaret came into the clinic today to be tested for …

But if instead your software replaced suspected names with synthetic names, it is not obvious when the software fails. When you see a reference to Margaret, you can’t know whether the patient’s name was Virginia and was replaced with Margaret or whether the software made an error skipped over Margaret’s name.

All else being equal, it’s better to synthesize names than remove names. But that doesn’t mean that just any process for synthesizing names will be adequate. The error rate doesn’t need to be zero, but it can’t be too high either. And the process should not be biased. If the software consistently left Hispanic names slip through, for example, Hispanic patients would not appreciate that.

Related posts

[1] “But what if I use a large language model?” That’s a particular kind of statistical inference.

[2] Any statistical test, such as testing whether a string of text represents a name, will have false positives (type I error) and false negatives (type II error). Software to remove names will remove some text that isn’t a name, and fail to recognize some text as names.

[3] We’ve tested a lot of deidentification software packages for clients, and the error rate is never zero. But privacy regulations such as HIPAA don’t require the error rate to be zero, only sufficiently small.

Typesetting Sha and Bitcoin

Posted on by John

I went down a rabbit hole this week using two symbols in LaTeX. The first was the Russian letter Sha (Ш, U+0248), and the second was the currency symbol for Bitcoin (₿, U+20BF).

Sha

I thought there would be a LaTeX package that would include Ш as a symbol rather than as a Russian letter, just as \pi produces π as a symbol rather than as a Greek letter per se, but apparently there isn’t. I was surprised, since Ш is used in math for at least three different things [1].

When I post on @TeXtip how to produce various symbols in LaTeX, I often get a reply telling me I should simply paste in the Unicode character and use XeTeX. That’s what I ended up doing, except one does not simply use XeTeX.

You have to set the font to one that contains a glyph for the character you want, and you have to use a font encoding package. I ended up adding these two lines to my file header:

    \usepackage[T2A]{fontenc}
    \usepackage{eulervm}

That worked, but only when I compiled with pdflatex, not xelatex.

Bitcoin

I ended up using a different but analogous tactic for the Bitcoin symbol. I used fontspec, Liberation Sans, and xelatex rather than fontenc, Euler, and pdflatex. These were the lines I added to the header:

    \usepackage{fontspec}
    \setmainfont{Liberation Sans}

Without these two lines I get the error message

    Missing character: There is no ₿ (U+20BF) in font ...

I didn’t need to use ₿ and Ш in the same document, but the approach in this section works for both. The approach in the previous section will not work for ₿ because the Euler font does not contain a gylph for ₿.

Related posts

[1] The three mathematical uses of Ш that I’m aware of are the shuffle product, the Dirac comb distribution, and Tate–Shafarevich group.

Golden powers revisited

Posted on by John

Years ago I wrote a post Golden powers are nearly integers. The post was picked up by Hacker News and got a lot of traffic. The post was commenting on a line from Terry Tao:

The powers φ, φ2, φ3, … of the golden ratio lie unexpectedly close to integers: for instance, φ11 = 199.005… is unusually close to 199.

In the process of writing my recent post on base-φ numbers I came across some equations that explain exactly why golden powers are nearly integers.

Let φ be the golden ratio and ψ = −1/φ. That is, φ and ψ are the larger and smaller roots of

x² − x − 1 = 0.

Then powers of φ reduce to an integer and an integer multiple of φ. This is true for negative powers of φ as well, and so powers of ψ also reduce to an integer and an integer multiple of ψ. And in fact, the integers alluded to are Fibonacci numbers.

φn = Fn φ + Fn − 1
ψn = Fn ψ + Fn − 1

These equations can be found in TAOCP 1.2.8 exercise 11.

Adding the two equations leads to [1]

φn = Fn + 1 + Fn − 1 − ψn

So yes, φn is nearly an integer. In fact, it’s nearly the sum of the (n + 1)st and (n − 1)st Fibonacci numbers. The error in this approximation is −ψn, and so the error decreases exponentially with alternating signs.

Related posts

[1] φn + ψn = Fn (φ + ψ) + 2 Fn − 1 = Fn + 2 Fn − 1 = Fn + Fn − 1 + Fn − 1 = Fn + 1 + Fn − 1

Naively computing sine

Posted on by John

Suppose you need to write software to compute the sine function. You were told in a calculus class that this is done using Taylor series—it’s not, but that’s another story—and so you start writing code to implement Taylor series.

How many terms do you need? Uh, …, 20? Let’s go with that.

from math import sin, factorial

def sine(x):
    s = 0
    N = 20
    for n in range(N//2):
        m = 2*n + 1
        s += (-1)**n * x**m / factorial(m)
    return s

You test your code against the built-in sin function and things look good.

    >>> sin(1)
    0.8414709848078965
    >>> sine(1)
    0.8414709848078965

Larger arguments

Next, just for grins, you try x = 100.

    >>> sin(100)
    -0.5063656411097588
    >>> sine(100)
    -7.94697857233433e+20

Hmm. Off by 20 orders of magnitude.

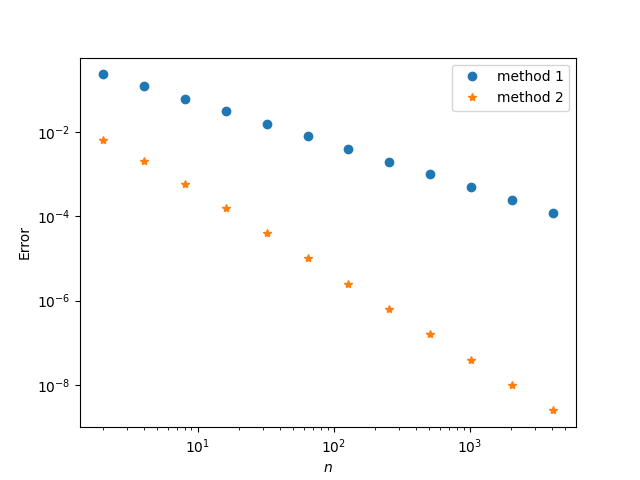
So you do a little pencil and paper calculation and determine that the code should work if you set N = 300 in the code above. You try again, and now you’re off by 25 orders of magnitude. And when you try entering 100.0 rather than 100, the program crashes.

What’s going on? In theory, setting N = 300 should work, according to the remainder term in the Taylor series for sine. But the largest representable floating point number is on the order of 10308 and so x**m terms in the code overflow. The reason the program didn’t crash when you typed in 100 with no decimal point is that Python executed x**m in integer arithmetic.

If you were patient and willing to use a huge number of terms in your Taylor series, you couldn’t include enough terms in your series to get accurate results for even moderately large numbers because overflow would kill you before you could get the series truncation error down. Unless you used extended precision floating point. But this would be using heroic measures to rescue a doomed approach.

Taylor series are good local approximations. They’re only valid within a radius of convergence; outside of that radius they’re worthless even in theory. Inside the radius they may be valid in theory but not in practice, as is the case above.

Range reduction

Taylor series isn’t the best approach for evaluating sine numerically, but you could make it work if you limited yourself to a small range of angles, say 0 to π/4, and used trig identities to reduce the general problem to computing sine in the range [0, π/4]. So how do you do that?

Let’s look at reducing arguments to live in the interval [0, 2π]. In practice you’d want to reduce the range further, but that requires keeping up with what quadrant you’re in etc. We’ll just consider [0, 2π] for simplicity.

The natural thing to do is subtract off the largest multiple of 2π you can.

    >>> from math import pi
    >>> k = int(100/(2*pi))
    >>> x = 100 - k*2*pi
    >>> sine(x)
    -0.5065317636696883
    >>> sin(100)
    -0.5063656411097588

That’s better. Now we don’t overflow, and we get three correct decimal places. We could increase N and get more. However, there’s a limit to how well we could do, as the calculation below shows.

    >>> sin(x)
    -0.5063656411097495
    >>> sin(100)
    -0.5063656411097588

When we reduce 100 mod 2π and call sin(x), we get a result that differs from sin(100) in the last three decimal places. That’s not terrible, depending on the application, but the loss of precision increases with the size of x and would be a complete loss for large enough values of x.

Let’s look back at where we divided 100 by 2π:

    >>> 100/(2*pi)
    15.915494309189533

When we throw away the integer part (15) and keep the rest (.915494309189533) we lose two figures of precision. The larger the integer part, the more precision we lose.

Our naive attempt at range reduction doesn’t work so well, but there are clever ways to make range reduction work. It is possible, for example, to compute the sine of a googol (i.e. sin 10100).

At first it seems simple to reduce the range. Then when you become aware of the precision problems and think about it a while, it seems precise range reduction is impossible. But if you keep thinking about it long enough you might find a way to make it work. A lot of effort went into range reduction algorithms years ago, and now they’re part of the computational infrastructure that we take for granted.

Computing the Euler-Mascheroni Constant

Posted on by John

The Euler-Mascheroni constant is defined as the limit

\gamma = \lim_{n\to\infty} \left(\sum_{k=1}^n \frac{1}{k} \right) - \log n

So an obvious way to try to calculate γ would be to evaluate the right-hand side above for large n. This turns out to not be a very good approach. Convergence is slow and rounding error accumulates.

A much better approach is to compute

\gamma = \lim_{n\to\infty} \left(\sum_{k=1}^n \frac{1}{k} \right) - \log\left( n + \tfrac{1}{2}\right)

It’s not obvious that you can add the extra factor of ½ in the log term, but you can: the right-hand sides of both equations above converge to γ, but the latter converges faster.

Here’s a comparison of the two methods.

The error in the first method with n = 4000 is comparable to the error in the second method with n = 16.

Even though the second equation above is better for numerical evaluation, there are much more sophisticated approaches. And this brings us to y-cruncher, software that has been used to set numerous world records for computing various constants. A new record for computing the digits of π was set a few weeks ago using y-cruncher. From the y-cruncher documentation:

Of all the things that y-cruncher supports, the Euler-Mascheroni Constant is the slowest to compute and by far the most difficult to implement. …

The Euler-Mascheroni Constant has a special place in y-cruncher. It is one of the first constants to be supported (even before Pi) and it is among the first for which a world record was set using y-cruncher. As such, y-cruncher derives its name from the gamma symbol for the Euler-Mascheroni Constant.

Posts involving γ

Golden ratio base numbers

Posted on by John

It is possible to express every positive integer as a sum of powers of the golden ratio φ using each power at most once. This means it is possible to create a binary-like number system using φ as the base with coefficients of 0 and 1 in front of each power of φ.

This system is sometimes called phinary because of the analogy with binary. I’ll use that term here rather than more formal names such as base-φ or golden base number system.

An interesting feature of phinary is that in general you need to include negative powers of φ to represent positive integers. For example,

2 = \varphi + \varphi^{-2}

and so you could write 2 in this system as 10.01.

To state things more formally, every positive integer n satisfies the following equation where a finite number of coefficients coefficients ak are equal to 1 and the rest are equal to 0.

n = \sum_{k=-\infty}^\infty a_k\varphi^k

The golden ratio satisfies φ² = φ + 1 and so phinary representations are not unique. But if you add the rule that number representations must not have consecutive 1s, then representations are unique, analogous to the Fibonacci number system.

The original paper describing the phinary system [1] is awkwardly written. It has the flavor of “Here are some examples. You can see how this generalizes.” rather than a more typical mathematical style.

The end of the article says “Jr. High School 246 Brooklyn, N.Y.” and so when I got to that point I thought the style was due to the paper having been written by a public school teacher rather than a professional mathematician. I later learned from [2] that the author was not a math teacher but a student: George Bergman was 12 years old when he discovered and published his number system.

Phinary is not as simple to develop as you might expect. Bergman’s discovery was impressive, and not only because he was 12 years old at the time. You can find more sophisticated developments in [2] and in [3], but both require a few preliminaries and are not simple.

***

[1] George Bergman. A Number System with an Irrational Base. Mathematics Magazine. 31 (2): 98–110. 1957.

[2] Cecil Rousseau. The Phi Number System Revisited. Mathematics Magazine, Vol. 68, No. 4 (Oct., 1995), pp. 283-284

[3] Donald Knuth. The Art of Computer Programming, volume 1.

Binomial number system

Posted on by John

I just stumbled across the binomial number system in Exercise 5.38 of Concrete Mathematics. The exercise asks the reader to show that every non-negative integer n can be written as

n = \binom{a}{1} + \binom{b}{2} + \binom{c}{3}

and that the representation is unique if you require 0 ≤ a < b < c. The book calls this the binomial number system. I skimmed a paper that said this has some application in signal processing, but I haven’t looked at it closely [1].

You can find a, b, and c much as you would find the representation in many other number systems: first find the largest possible c, then the largest possible b for what’s left, and then the remainder is a.

In order to find c, we start with the observation that the binomial coefficient C(k, 3) is less than k³/6 and so c is less than the cube root of 6n. We can use this as an initial lower bound on c then search incrementally. If we wanted to be more efficient, we could do some sort of binary search.

Here’s Python code to find a, b, and c.

from math import comb, factorial

def lower(n, r):
    "Find largest k such that comb(k, r) <= n."
    k = int( (factorial(r)*n)**(1/r) ) # initial guess
    while comb(k, r) <= n: 
        k += 1 
    return k - 1 

def binomial_rep(n): 
    c = lower(n, 3) 
    cc = comb(c, 3) 
    b = lower(n - comb(c, 3), 2) 
    bb = comb(b, 2) 
    a = n - cc - bb 
    assert(c > b > a >= 0)
    return (a, b, c)

For example, here’s the binomial number system representation of today’s date.

>>> binomial_rep(20250605)
(79, 269, 496)
>>> comb(496, 3) + comb(269, 2) + comb(79, 1)
20250605

You could use any number of binomial terms, not just three.

[1] I looked back at the paper, and it is using a different kind of binomial number system, expressing numbers as sums of fixed binomial coefficients, not varying the binomial coefficient arguments. This representation has some advantages for error correction.

Additive and multiplicative persistence

Posted on by John

Casting out nines is a well-known way of finding the remainder when a number is divided by 9. You add all the digits of a number n. And if that number is bigger than 9, add all the digits of that number. You keep this up until you get a number less than 9.

This is an example of persistence. The persistence of a number, relative to some operation, is the number of times you have to apply that operation before you reach a fixed point, a point where applying the operation further makes no change.

The additive persistence of a number is the number of times you have to take the digit sum before getting a fixed point (i.e. a number less than 9). For example, the additive persistence of 8675309 is 3 because the digits in 8675309 sum to 38, the digits in 38 sum to 11, and the digits in 11 sum to 2.

The additive persistence of a number in base b is bounded above by its iterated logarithm in base b.

The smallest number with additive persistence n is sequence A006050 in OEIS.

Multiplicative persistence is analogous, except you multiply digits together. Curiously, it seems that multiplicative persistence is bounded. This is true for numbers with less than 30,000 digits, and it is conjectured to be true for all integers.

The smallest number with multiplicative persistence n is sequence A003001 in OEIS.

Here’s Python code to compute multiplicative persistence.

def digit_prod(n):
    s = str(n)
    prod = 1
    for d in s:
        prod *= int(d)
    return prod

def persistence(n):
    c = 0
    while n > 9:
        n = digit_prod(n)
        print(n)
        c += 1
    return c

You could use this to verify that 277777788888899 has persistence 11. It is conjectured that no number has larger persistence larger than 11.

The persistence of a large number is very likely 1. If you pick a number with 1000 digits at random, for example, it’s very likely that at least of these digits will be 0. So it would seem that the probability of a large number having persistence larger than 11 would be incredibly small, but I would not have expected it to be zero.

Here are plots to visualize the fixed points of the numbers less than N for increasing values of N.


It’s not surprising that zeros become more common as N increases. And a moments thought will explain why even numbers are more common than odd numbers. But it’s a little surprising that 4 is much less common than 2, 6, or 8.

Incidentally, we have worked in base 10 so far. In base 2, the maximum persistence is 1: when you multiply a bunch of 0s and 1s together, you either get 0 or 1. It is conjectured that the maximum persistence in base 3 is 3.