Computing

Converse of RSA

Posted on by John

The security of RSA encryption depends on the difficulty of factoring the product of two large primes. If you can factor large numbers efficiently, you can break RSA. But if can break RSA, can you factor large numbers?

Sorta. It’s conceivable that there is a way to break RSA encryption without having to recover the private key. But if you can recover the private key, then you can factor efficiently. That is, if you can start with a public key (N, e), where N is the modulus and e is the encryption key, and recover the private key d, then you can efficiently factor N. See “Fact 1” in [1].

Let n = log2 N. Then the algorithm alluded to above can be run in O(n³) time. But the best known factoring algorithms take more than O(exp(n1/3)) time.

Related posts

[1] Dan Boneh. Twenty Years of Attacks on the RSA Cryptosystem. Available here.

Details of generating primes for cryptography

Posted on by John

RSA public key cryptography begins by finding a couple large primes. You essentially do this by testing random numbers until you find primes, but not quite.

Filippo Valsorda just posted a good article on this.

Suppose you’re looking for a 1024-bit prime number. You generate random 1024-bit numbers and then test until you find one that’s prime. You can immediately make this process twice as fast by setting the last bit to 1: it would be wasteful to generate a new number every time you happened to draw an even number.

A little less obvious is that it’s common to set the top bit as well. When you’re generating a number between 0 and 21024 − 1, it’s possible that you could generate a small number. It’s possible that you generate a very small number, like 59, but extremely unlikely. But it’s not so unlikely that you’d generate a number on the order of 21020, for example. By setting the top bit, you know you’re generating a number between 21023 and 21024.

Most composite numbers have small factors, so you check for divisibility by 3, 5, 7 etc. before running more time-consuming tests. Probabilistic tests are far more efficient than deterministic tests, so in practice everyone uses probable primes in RSA. For details of how you apply these tests, and how many tests to run, see Filippo Valsorda’s article.

Should you be concerned about setting the top bit of prime candidates? There are naive and sophisticated reasons not work worry, and an intermediate reason to at least think about it.

The naive response is that you’re just losing one bit of randomness. How much could that hurt? But in other contexts, such as losing one bit of randomness in an AES key, people do worry about such losses.

The bits in the prime factors of an RSA modulus do not correspond directly to bits of security. A 2048-bit modulus, the product of two 1024-bit primes, has about 112 bits of security. (See NIST SP 800-57.) You could set several bits in your prime factors before losing a bit of security. If this bothers you, move up to using a 3072-bit modulus rather than worrying that you 2048-bit modulus is in a sense a 2046-bit modulus.

More cryptography posts

Unix Time and a Modest Proposal

Posted on by John

The time it takes earth to orbit the sun is not a simple multiple of the time it takes earth to rotate on its axis. The ratio isn’t even constant. The time it takes earth to circle the sun wobbles a bit, and the rotation of the earth is slowing down slightly.

The ratio is around 365.2422. Calling it 365 is too crude. Julius Caesar said we should call it 365 1/4, and that was good enough for a while. Then Pope Gregory said we really should use 365 97/400, and that’s basically good enough, but not quite. More on that here.

Leap seconds

In 1972 we started adding leap seconds in order to synchronize the day and the year more precisely. Unlike leap days, leap seconds don’t occur on a strict schedule. A leap second is inserted when a committee of astronomers decides one should be inserted, about every two years.

An international standards body has decided to stop adding leap seconds by 2035. They cause so confusion that it was decide that letting the year drift by a few seconds was preferable.

Unix time

Unix time is the number of seconds since the “epoch,” i.e. January 1, 1970, sorta.

If you were to naively calculate Unix time for this coming New Year’s Day, you’d get the right result.

New Year’s Day 2025

When New Year’s Day 2025 begins in England, the Unix time will be

(55 × 365 + 14) × 24 × 60 × 60 = 1735689600

This because there are 55 years between 1970 and 2025, 14 of which were leap years.

However, that moment will be 1735689627 seconds after the epoch.

Non-leap seconds

Unix time is the number of non-leap seconds since 1970-01-01 00:00:00 UTC. There have been 27 leap seconds since 1970, and so Unix time is 27 seconds behind elapsed time.

Leap year analogy

You could think of a second in Unix time as being 1/86400 th of a day. Every day has 86400 non-leap seconds, but some days have had 86401 seconds. A leap second could potentially be negative, though this has not happened yet. A day containing a negative leap second would have 86399 seconds.

The analogous situation for days would be to insist that every year have 365 days. February 28 would be the 59th day of the year, and March 1 would be the 60th day, even in a leap year.

International Atomic Time

What if you wanted a time system based on the actual number of elapsed seconds since the epoch? This is almost what International Atomic Time is.

International Atomic Time (abbreviated TAI, from the French temps atomique international) is ahead of UTC [1] by 37 seconds, not 27 seconds as you might expect. Although there have been 27 leap seconds since 1972, TAI dates back to 1958.

So New Year’s Day will start in England at 2025-01-01 00:00:37 TAI.

A Modest Proposal

It seems our choices are to add leap seconds and endure the resulting confusion, or not add leap seconds and allow the year to drift with respect to the day. There is a third way: adjust the position of the earth periodically to keep the solar year equal to an average Gregorian calendar day. I believe this modest proposal [2] deserves consideration.

Kepler’s law says the square of a planet’s orbital period is proportional to the cube of the semi-major axis of its orbit. This means that increasing earth’s orbital period by 1 second would only require moving earth 3.16 km further from the sun.

***

[1] UTC stands for Universal Coordinated Time. From an earlier post,

The abbreviation UTC is an odd compromise. The French wanted to use the abbreviation TUC (temps universel coordonné) and the English wanted to use CUT (coordinated universal time). The compromise was UTC, which doesn’t actually abbreviate anything.

[2] In case you’re not familiar with the term “modest proposal,” it comes from the title of a satirical essay by Jonathan Swift. A modest proposal has come to mean an absurdly simple solution to a complex problem presented satirically.

Can AI models reason: Just a stochastic parrot?

Posted on by Wayne Joubert

OpenAI has just released its full o1 model—a new kind of model that is more capable of multi-step reasoning than previous models. Anthropic, Google and others are no doubt working on similar products. At the same time, it’s hotly debated in many quarters whether AI models actually “reason” in a way similar to humans.

Emily Bender and her colleagues famously described large language models as nothing more than “stochastic parrots“—systems that simply repeat their training data blindly, based on a statistical model, with no real understanding (reminiscent of the Chinese Room experiment). Others have made similar comments, describing LLMs as “n-gram models on steroids” or a “fancy extrapolation algorithm.”

There is of course some truth to this. AI models sometimes generate remarkable results and yet lack certain basic aspects of understanding that might inhibit their sometimes generation of nonsensical results. More to the point of “parroting” the training data, recent work from Yejin Choi’s group has shown how LLMs at times will cut and paste snippets from its various training documents, almost verbatim, to formulate its outputs.

Are LLMs (just) glorified information retrieval tools?

The implication of these concerns is that an LLM can “only” repeat back what it was taught (albeit with errors). However this view does not align with the evidence. LLM training is a compression process in which new connections between pieces of information are formed that were not present in the original data. This is evidenced both mathematically and anecdotally. In my own experience, I’ve gotten valid answers to such obscure and detailed technical question that it is hard for me to believe would exist in any training data in exactly that form. Whether you would call this “reasoning” or not might be open to debate, but regardless of what you call it, it is something more than just unadorned information retrieval like a “stochastic parrot.”

What is your experience? Let us know in the comments.

Interval arithmetic and fixed points

Posted on by John

A couple days ago I analyzed the observation that repeatedly pressing the cosine key on a calculator leads to a fixed point. After about 90 iterations the number no longer changes. This post will analyze the same phenomenon a different way.

Interval arithmetic

Interval arithmetic is a way to get exact results of a sort from floating point arithmetic.

Suppose you start with a number x that cannot be represented exactly as a floating point number, and you want to compute f(x) for some function f. You can’t represent x exactly, but unless x is too large you can represent a pair of numbers a and b such that x is certainly in the interval [a, b]. Then f(x) is in the set f( [a, b] ).

Maybe you can represent f( [a, b] ) exactly. If not, you can enlarge the interval a bit to exactly represent an interval that contains f(x). After applying several calculations, you have an interval, hopefully one that’s not too big, containing the exact result.

(I said above that interval arithmetic gives you exact results of a sort because even though you don’t generally get an exact number at the end, you do get an exact interval containing the result.)

Cosine iteration

In this post we will use interval arithmetic, not to compensate for the limitations of computer arithmetic, but to illustrate the convergence of iterated cosines.

The cosine of any real number lies in the interval [−1, 1]. To put it another way,

cos( [−∞, ∞] ) = [−1, 1].

Because cosine is an even function,

cos( [−1, 1] ) = cos( [0, 1] )

and so we can limit our attention to the interval [0, 1].

Now the cosine is a monotone decreasing function from 0 to π, and so it’s monotone on [0, 1]. For any two points with 0 ≤ a ≤ b ≤ π we have

cos( [a, b] ) = [cos(b), cos(a)].

Note that the order of a and b reverses on the right hand side of the equation because cosine is decreasing. When we apply cosine again we get back the original order.

cos(cos( [a, b] )) = [cos(cos(a)), cos(cos(b))].

Incidentally, this flip-flop explains why the cobweb plot from the previous post looks like a spiral rather than a staircase.

Now define a0 = 0, b0 = 1, and

[an+1, bn+1] = cos( [an, bn] ) = [cos(bn), cos(an)].

We could implement this in Python with a pair of mutually recursive functions.

    a = lambda n: 0 if n == 0 else cos(b(n-1))
    b = lambda n: 1 if n == 0 else cos(a(n-1))

Here’s a plot of the image of [0, 1] after n iterations.

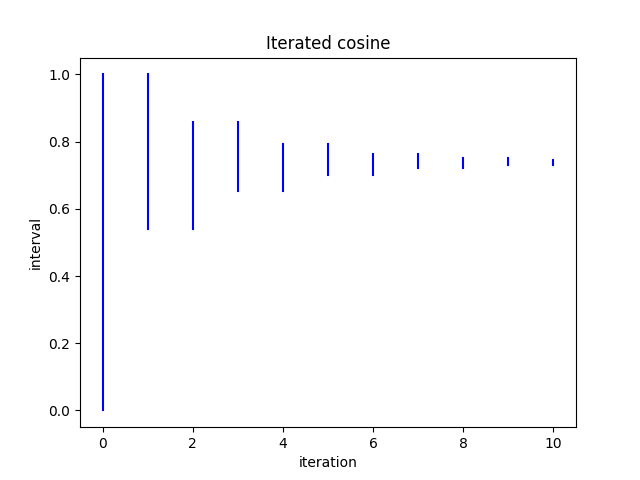
Note that odd iterations increase the lower bound and even iterations decrease the upper bound.

Numerical interval arithmetic

This post introduced interval arithmetic as a numerical technique, then proceeded to do pure math. Now let’s think about computing again.

The image of [0, 1] under cosine is [cos(1), cos(0)] = [cos(1), 1]. A computer can represent 1 exactly but not cos(1). Suppose we compute

cos(1) = 0.5403023058681398

and assume each digit in the result is correct. Maybe the exact value of cos(1) was slightly smaller and was rounded to this value, but we know for sure that

cos( [0, 1] ) ⊂ [0.5403023058681397, 1]

So in this case we don’t know the image of [0, 1], but we know an interval that contains the image, hence the subset symbol.

We could iterate this process, next computing an interval that contains

cos( [0.5403023058681397, 1] )

and so forth. At each step we would round the left endpoint down to the nearest representable lower bound and round the right endpoint up to the nearest representable upper bound. In practice we’d be concerned with machine representable numbers rather than decimal representable numbers, but the principle is the same.

The potential pitfall of interval arithmetic in practice is that intervals may grow so large that the final result is not useful. But that’s not the case here. The rounding error at each step is tiny, and contraction maps reduce errors at each step rather than magnifying them. In a more complicated calculation, we might have to resort to lose estimates and not have such tight intervals at each step.

Related posts

Golden hospital gowns

Posted on by John

Here’s something I posted on X a couple days ago:

There’s no direct connection between AI and cryptocurrency, but they have a similar vibe.

They both leave you wondering whether the emperor is sumptuously clothed, naked, or a mix of both.

Maybe he’s wearing a hospital gown with gold threads.

In case you’re unfamiliar with the story, this is an allusion to The Emperor’s New Clothes, one of the most important stories in literature.

I propose golden hospital gown as a metaphor for things that are a fascinating mixture of good and bad, things that have large numbers of haters and fanboys, both with valid points. There’s continual improvement and a lot work to be done sorting out what works well and what does not.

I tried to get Grok to create an image of what I had in mind by a golden hospital gown. The results were not what I wanted, but passable, which is kinda the point of the comment above. It’s amazing that AI can produce anything remotely resembling a desired image starting from a text description. But there is a very strong temptation to settle for mediocre and vaguely creepy images that aren’t what we really want.

Man in a yellow hospital gown with hairy back and legs exposed

Related posts

LLMs and regular expressions

Posted on by John

Yesterday I needed to write a regular expression as part of a client report. Later I was curious whether an LLM could have generated an equivalent expression.

When I started writing the prompt, I realized it wasn’t trivial to tell the LLM what I wanted. I needed some way to describe the pattern that the expression should match.

“Hmm, what’s the easiest way to describe a text pattern? I know: use a regular expression! Oh wait, …”

Prompt engineering and results

I described the pattern in words, which was more difficult than writing the regular expression, and the LLM came up with a valid regular expression, and sample code for demonstrating the use of the expression, but the expression wasn’t quite right. After a couple more nudges I managed to get it to produce a correct regex.

I had asked for a Perl regular expression, and the LLM did generate syntactically correct Perl [1], both for the regex and the sample code. When I asked it to convert the regex to POSIX form it did so, and when I asked it to convert the regex to Python it did that as well, replete with valid test code.

I repeated my experiment using three different LLMs and got similar results. In all cases, the hardest part was specifying what I wanted. Sometimes the output was correct given what I asked for but not what I intended, a common experience since the dawn of computers. It was easier to translate a regex from one syntax flavor to another than to generate a correct regex, easier for both me and the computer: it was easier for me to generate a prompt and the LLM did a better job.

Quality assurance for LLMs

Regular expressions and LLMs are complementary. The downside of regular expressions is that you have to specify exactly what you want. The upside is that you can specify exactly what you want. We’ve had several projects lately in which we tested the output of a client’s model using regular expressions and found problems. Sometimes it takes a low-tech tool to find problems with a high-tech tool.

We’ve also tested LLMs using a different LLM. That has been useful because there’s some degree of independence. But we’ve gotten better results using regular expressions since there is a greater degree of independence.

Related posts

[1] Admittedly that’s a low bar. There’s an old joke that Perl was created by banging on a keyboard then hacking on the compiler until the input compiled.

Rotating MacBook keys

Posted on by John

Shortly after I started using a MacBook I remapped the keys so that they function the same way on Mac OS, Windows, and Linux. The key in the lower left corner, for example, behaves the same way across operating systems, as does the key to the left of the space bar.

Note that I’m going by key behavior and not key name. I go into more detail in my post on cross-platform muscle memory.

It’s been two and a half years since I remapped the keys, and it works well for me. The same keystrokes do the same thing whether I’m on my MacBook laptop or my Linux desktop.

The only drawback is that I’m confused when read documentation telling me how to do something on a Mac. When I see something using the ⌘ key, I have to ask myself which key that corresponds to on my machine. I’m writing this post in hopes that it will help me memorize how my mappings relate to the original keys.

Here’s a diagram of how I have rotated my keys.

command to fn to option to command

So, for example, if I want to make text bold, I hold down the key in the lower left corner and type b. On my MacBook that key is labeled with a globe and on my Linux box it is labeled Ctrl. But I don’t look at the keys and don’t care what they’re labeled.

I also swapped the Caps Lock and what Mac calls the control key ⌃, but I mostly use the big control key only in Emacs. As I noted in the earlier article, Mac essentially has one Windows-like control key (labeled ⌘) and one Emacs-like control key (labeled control).

 

 

Asymmetric generation / verification costs

Posted on by John

We tend to think that the effort required to generate a solution and verify a solution are roughly equal, assuming that you need to retrace the generation steps to verify that they are correct. But sometimes verification can be far easier than generation [1].

Factoring

For example, suppose I generate two 1000-digit prime numbers, multiply them together, and ask you to recover the two primes by factoring. It takes a split second to verify whether you’ve found the solution, but finding the solution is practically impossible. The security of the internet depends on this fact. (See posts on RSA encryption here.)

Generative AI

Generative AI is notoriously unreliable. But if it’s far easier to verify a solution than to generate it, it’s OK if an AI solution is unreliable. We’ve had several consulting projects lately that amount to evaluating how well an LLM did what it was supposed to do. The LLMs aren’t perfect—no one expected that they would be—but the tasks is to estimate whether the error rate is acceptable.

Differential equations

George Pólya once said “In order to solve a differential equation you look at it till a solution occurs to you.” He was only half joking. Differential equations courses present solution techniques without justification [2], but the solutions can be justified even if they techniques cannot: stick the solution in to the equation and see whether it works.

Finding primes

For the last 70 years, the largest known prime has been a Mersenne prime, with one exception [3]. This is because there is a way to test whether Mersenne numbers are prime that is more efficient than general numbers.

It takes a lot of computation to prove that a large number is prime, but it is possible to produce a certificate of primality that can be quickly verified. One form of primality certificate is Pratt certificates and another kind is elliptic curve primality certificates.

Optimization

Some optimization problems, such as linear programming or more generally convex optimization, produce certificates that verify that a solution is optimal. Maybe the solution was found on a beefy computer but could be verified on a phone.

Lack of solution

It’s typically easier to prove a solution exists than to prove a solution does not exist. You can prove a solution exists by finding one. This may not be easy to do but easy to verify. Certifying that a problem as no solution is more difficult—how do you know whether you’ve looked hard enough?—but sometimes you can produce a certificate of infeasibility.

Footnotes

[1] The question of whether P = NP asks whether in some sense it is possible to efficiently compute solutions to a large class of problems whose solutions can be verified efficiently [4].

[2] The solution techniques can be justified, though not at the level of mathematics students have when taking an introductory differential equations course.

[3] In 1989 the largest known prime was 391581 × 2216193 − 1.

[4] Can a footnote have a footnote? Sure, why not. The P = NP problem asks whether a problem that can be verified in polynomial time can be solved in polynomial time. But if you didn’t already know this, you probably won’t find this description satisfying. It’s kinda subtle, and I won’t add a footnote to a footnote of a footnote.

Confidential OCR

Posted on by John

A client emailed me a screenshot of a table rather than pasting the table as text into an email.

I thought about using an LLM to convert it to text, but the table is confidential client information and so I shouldn’t upload it anywhere.

I searched for a commandline utility to do OCR and found tesseract. I installed it with

    sudo apt install tesseract-ocr libtesseract-dev tesseract-ocr-eng

and ran it with the default settings

    tesseract screenshot.png textfile

It worked remarkably well. I had to change a C to a U, but otherwise I didn’t have to add or change any text, but I did have to delete a few extraneous parentheses generated by the software.

I work locally in part out of habit; it was the only way to work when I started using a computer. It has numerous advantages, such as being able to keep working when a hurricane knocks out my internet connection, but above all it is private.

I pay more attention to privacy than is convenient because I work in data privacy. And aside from my privacy, I have to protect our clients’ privacy.

Update: According to the comments, ChatGPT uses tesseract. Assuming that’s true, using tesseract directly is better than ChatGPT because it does exactly what you want. No ambiguity as far as what expected. No potential for tinkering with your results before you see them.

Related posts