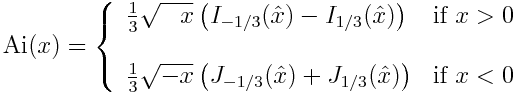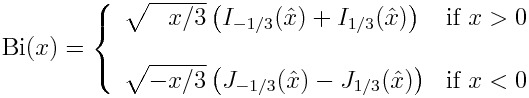Ellipsoid surface area

Posted on 6 July 2014 by John

How much difference does the earth’s equatorial bulge make in its surface area?

To first approximation, the earth is a sphere. The next step in sophistication is to model the earth as an ellipsoid.

The surface area of an ellipsoid with semi-axes a ≥ b ≥ c is

$A = 2\pi \left( c^2 + \frac{ab}{\sin\phi} \left( E(\phi, k) \sin^2\phi + F(\phi, k) \cos^2 \phi\right)\right)$

where

$\cos \phi = \frac{c}{a}$

and

$m = k^2 = \frac{a^2(b^2 - c^2)}{b^2(a^2 - c^2)}$

The functions E and F are incomplete elliptic integrals

$F(\phi, k) = \int_0^\phi \frac{d\theta}{\sqrt{1 - k^2 \sin^2\theta}}$

and

$E(\phi, k) = \int_0^\phi \sqrt{1 - k^2 \sin^2\theta}\,d\theta$

implemented in SciPy as ellipeinc and ellipkinc. Note that the SciPy functions take m as their second argument rather its square root k.

For the earth, a = b and so m = 1.

The following Python code computes the ratio of earth’s surface area as an ellipsoid to its area as a sphere.

from numpy import pi, sin, cos, arccos
from scipy.special import ellipkinc, ellipeinc

# values in meters based on GRS 80
# https://en.wikipedia.org/wiki/GRS_80
equatorial_radius = 6378137
polar_radius = 6356752.314140347

a = b = equatorial_radius
c = polar_radius

phi = arccos(c/a)
# in general, m = (a**2 * (b**2 - c**2)) / (b**2 * (a**2 - c**2))
m = 1

temp = ellipeinc(phi, m)*sin(phi)**2 + ellipkinc(phi, m)*cos(phi)**2
ellipsoid_area = 2*pi*(c**2 + a*b*temp/sin(phi))

# sphere with radius equal to average of polar and equatorial
r = 0.5*(a+c)
sphere_area = 4*pi*r**2

print(ellipsoid_area/sphere_area)

This shows that the ellipsoid model leads to 0.112% more surface area relative to a sphere.

Source: See equation 19.33.2 here.

Update: It was suggested in the comments that it would be better to compare the ellipsoid area to that of a sphere of the same volume. So instead of using the average of the polar and equatorial radii, one would take the geometric mean of the polar radius and two copies of the equatorial radius. Using that radius, the ellipsoid has 0.0002% more area than the sphere.

Update 2: This post gives a simple but accurate approximation for the area of an ellipsoid.

Relating Airy and Bessel functions

Posted on 1 September 2013 by John

The Airy functions Ai(x) and Bi(x) are independent solutions to the differential equation

For negative x they act something like sin(x) and cos(x). For positive x they act something like exp(x) and exp(−x). This isn’t surprising if you look at the differential equation. If you replace x with a negative constant, you get sines and cosines, and if you replace it with a positive constant, you get positive and negative exponentials.

The Airy functions can be related to Bessel functions as follows:

$\mathrm{Ai}(x) = \left\{ \begin{array}{ll} \frac{1}{3}\sqrt{\phantom{-}x} \left(I_{-1/3}(\hat{x}) - I_{1/3}(\hat{x})\right) & \mbox{if } x > 0 \\ \\ \frac{1}{3}\sqrt{-x} \left(J_{-1/3}(\hat{x}) + J_{1/3}(\hat{x})\right) & \mbox{if } x < 0 \end{array} \right.$

and

$\mathrm{Bi}(x) = \left\{ \begin{array}{ll} \sqrt{\phantom{-}x/3} \left(I_{-1/3}(\hat{x}) + I_{1/3}(\hat{x})\right) & \mbox{if } x > 0 \\ \\ \sqrt{-x/3} \left(J_{-1/3}(\hat{x}) - J_{1/3}(\hat{x})\right) & \mbox{if } x < 0 \end{array} \right.$

Here J is a “Bessel function of the first kind” and I is a “modified Bessel function of the first kind.” Also

$\hat{x} = \frac{2}{3} \left(\sqrt{|x|}\right)^3$

To verify the equations above, and to show how to compute these functions in Python, here’s some code.

The SciPy function airy computes both functions, and their first derivatives, at once. I assume that’s because it doesn’t take much longer to compute all four functions than to compute one. The code for Ai2 and Bi2 below uses np.where instead of if … else so that it can operate on NumPy vectors all at once. You can plot Ai and Ai2 and see that the two curves lie on top of each other. The same holds for Bi and Bi2.

from scipy.special import airy, jv, iv
from numpy import sqrt, where

def Ai(x):
    (ai, ai_prime, bi, bi_prime) = airy(x)
    return ai

def Bi(x):
    (ai, ai_prime, bi, bi_prime) = airy(x)
    return bi

def Ai2(x):
    third = 1.0/3.0
    hatx = 2*third*(abs(x))**1.5
    return where(x > 0,
        third*sqrt( x)*(iv(-third, hatx) - iv(third, hatx)),
        third*sqrt(-x)*(jv(-third, hatx) + jv(third, hatx)))

def Bi2(x):
    third = 1.0/3.0
    hatx = 2*third*(abs(x))**1.5
    return where(x > 0,
        sqrt( x/3.0)*(iv(-third, hatx) + iv(third, hatx)),
        sqrt(-x/3.0)*(jv(-third, hatx) - jv(third, hatx)))

There is a problem with Ai2 and Bi2: they return nan at 0. A more careful implementation would avoid this problem, but that’s not necessary since these functions are only for illustration. In practice, you’d simply use airy and it does the right thing at 0.

Related links:

Ramanujan approximation for circumference of an ellipse

Posted on 5 May 2013 by John

There’s no elementary formula for the circumference of an ellipse, but there is an elementary approximation that is extremely accurate.

An ellipse has equation (x/a)² + (y/b)² = 1. If a = b, the ellipse reduces to a circle and the circumference is simply 2πa. But the general formula for circumference requires the hypergeometric function ₂F₁:

$\setlength\arraycolsep{1pt} \pi (a + b) \, {}_2 F_1\left(\begin{matrix}-1/2& &-1/2 \\&1& \end{matrix}\middle;\lambda^2\right)$

where λ = (a − b)/(a + b).

However, if the ellipse is anywhere near circular, the following approximation due to Ramanujan is extremely good:

$\pi (a + b) \left(1 + \frac{3\lambda^2}{10 + \sqrt{4 - 3\lambda^2}}\right)$

To quantify what we mean by extremely good, the error is O(λ¹⁰). When an ellipse is roughly circular, λ is fairly small, and the error is on the order of λ to the 10th power.

To illustrate the accuracy of the approximation, I tried the formula out on some planets. The error increases with ellipticity, so I took the most elliptical orbit of a planet or object formerly known as a planet. That distinction belongs to Pluto, in which case λ = 0.016. If Pluto’s orbit were exactly elliptical, you could use Ramanujan’s approximation to find the circumference of its orbit with an error less than one micrometer.

Next I tried it on something with a much more elliptical orbit: Halley’s comet. Its orbit is nearly four times longer than it is wide. For Halley’s comet, λ = 0.59 and Ramanujan’s approximation agrees with the exact result to seven significant figures. The exact result is 11,464,319,022 km and the approximation is 11,464,316,437 km.

Here’s a video showing how elliptical the comet’s orbit is.

If you’d like to experiment with the approximation, here’s some Python code:

    from scipy import pi, sqrt
    from scipy.special import hyp2f1

    def exact(a, b):
        t = ((a-b)/(a+b))**2
        return pi*(a+b)*hyp2f1(-0.5, -0.5, 1, t)

    def approx(a, b):
        t = ((a-b)/(a+b))**2
        return pi*(a+b)*(1 + 3*t/(10 + sqrt(4 - 3*t)))

    # Semimajor and semiminor axes for Halley's comet orbit
    a = 2.667950e9 # km
    b = 6.782819e8 # km

    print exact(a, b)
    print approx(a, b)

Rolling dice for normal samples: Python version

Posted on 29 April 2013 by John

A handful of dice can make a decent normal random number generator, good enough for classroom demonstrations. I wrote about this a while ago.

My original post included Mathematica code for calculating how close to normal the distribution of the sum of the dice is. Here I’d like to redo the code in Python to show how to do the same calculations using SymPy. [Update: I’ll also give a solution that does not use SymPy and that scales much better.]

If you roll five dice and add up the spots, the probability of getting a sum of k is the coefficient of x^k in the expansion of

(x + x² + x³ + x⁴ + x⁵ + x⁶)⁵ / 6⁵.

Here’s code to find the probabilities by expanding the polynomial and taking coefficients.

    from sympy import Symbol

    sides = 6
    dice = 5
    rolls = range( dice*sides + 1 )

    # Tell SymPy that we want to use x as a symbol, not a number
    x = Symbol('x')

    # p(x) = (x + x^2 + ... + x^m)^n
    # where m = number of sides per die
    # and n = number of dice
    p = sum( x**i for i in range(1, sides + 1) )**dice

    # Extract the coefficients of p(x) and divide by sides**dice
    pmf = [sides**(-dice) * p.expand().coeff(x, i) for i in rolls]

If you’d like to compare the CDF of the dice sum to a normal CDF you could add this.

    from scipy import array, sqrt
    from scipy.stats import norm

    cdf = array(pmf).cumsum()

    # Normal CDF for comparison
    mean = 0.5*(sides + 1)*dice
    variance = dice*(sides**2 -1)/12.0
    temp = [norm.cdf(i, mean, sqrt(variance)) for i in roles]
    norm_cdf = array(temp)

    diff = abs(cdf - norm_cdf)
    # Print the maximum error and where it occurs
    print diff.max(), diff.argmax()

Question: Now suppose you want a better approximation to a normal distribution. Would it be better to increase the number of dice or the number of sides per dice? For example, would you be better off with 10 six-sided dice or 5 twelve-sided dice? Think about it before reading the solution.

Update: The SymPy code does not scale well. When I tried the code with 50 six-sided dice, it ran out of memory. Based on Andre’s comment, I rewrote the code using polypow. SymPy offers much more symbolic calculation functionality than NumPy, but in this case NumPy contains all we need. It is much faster and it doesn’t run out of memory.

    from numpy.polynomial.polynomial import polypow
    from numpy import ones

    sides = 6
    dice = 100

    # Create an array of polynomial coefficients for
    # x + x^2 + ... + x^sides
    p = ones(sides + 1)
    p[0] = 0

    # Extract the coefficients of p(x)**dice and divide by sides**dice
    pmf = sides**(-dice) * polypow(p, dice)
    cdf = pmf.cumsum()

That solution works for up to 398 dice. What’s up with that? With 399 dice, the largest polynomial coefficient overflows. If we divide by the number of dice before raising the polynomial to the power dice, the code becomes a little simpler and scales further.

    p = ones(sides + 1)
    p[0] = 0
    p /= sides
    pmf = polypow(p, dice)
    cdf = pmf.cumsum()

I tried this last approach on 10,000 dice with no problem.

New introduction to SciPy

Posted on 29 March 2013 by John

The Python stack for scientific computing is more modular than say R or Mathematica. Python is a general-purpose programming language that has libraries for scientific computing. R and Mathematica are statistical and mathematical programming languages that have general-purpose features. The Python approach has its advantages — I’d rather do math in a general language than do general programming in a mathematical language — but it takes longer to learn. The components of the Python stack work well together, but someone new to Python has to discover what components they’ll need.

Several books have come out recently to help someone learn Python and the components for numerical computing. The latest is Learning SciPy for Numerical and Scientific Computing [link rot] by Francisco J. Blanco-Silva.

This book covers the things you’d expect, including SciPy, NumPy, and Matplotlib. The only exception may be IPython. But no book can cover everything. And since IPython is an environment more than a library, it makes some sense to leave it out.

In addition to the usual topics, the book includes several important topics that are not as commonly covered. For example, it devotes a good amount of space to special functions and integration in a chapter on numerical analysis. I share the author’s assessment that this is “one of the most interesting chapters in the book.”

There are three chapters on more specific applications: signal processing, data mining, and computational geometry. These chapters give an introduction to their topics as well as how to carry out computations in SciPy.

The final chapter of the book is on integration with other programming languages.

Learning SciPy for Numerical and Scientific Computing covers the material you need to get going. It’s easy to read, and still fairly small: 150 pages total, about 130 pages of content. This is the right size for such a book in my opinion. There’s plenty of online documentation for more details, but it helps to have a good overview such as this book before diving into reference material.

Three new Python books

Posted on 11 December 2012 by John

This post reviews three Python books that have come out recently:

SciPy and NumPy from O’Reilly
Python for Kids: A Playful Introduction to Programming from No Starch Press
NumPy Cookbook from Packt

SciPy and NumPy (ISBN 1449305466) by Eli Bressert is the smallest book I’ve seen from O’Reilly, aside from books in their pocket guide series. The SciPy and NumPy libraries are huge, and it can be hard to know where to start. This book gives a good, brisk overview. In addition to SciPy and NumPy, the it also gives a brief introduction to SciKit, in particular scikit-learn for machine learning and scikit-image for image processing.

(Eli told me that he is working on supplementary material for the book. Everyone who bought the book electronically will automatically receive the new material when it is available.)

Python for Kids (ISBN 1593274076) by Jason R. Briggs is an introduction to programming aimed at kids. It starts with an introduction to Python and moves to developing a simple game. It seems to me that kids would find the book interesting. It’s about seven times longer than the SciPy and NumPy book. It moves at a slow pace, has many illustrations, and has a casual tone.

NumPy Cookbook by Ival Idris contains around 70 small recipes, about three pages each. Many of these are about NumPy itself, but the book covers much more than its title would imply. Out of 10 chapters, four are strictly about NumPy. The first chapter of the book is about IPython. Another chapter is about “connecting NumPy with the rest of the world,” i.e. interfacing with Java, R, Matlab, and cloud services. Two chapters are devoted to profiling, debugging, and optimizing performance. There is a chapter on quality assurance (static analysis, unit testing, and documentation). And the final chapter is about Scikits and Pandas.

Winston Churchill, Bessie Braddock, and Python

Posted on 29 November 2012 by John

Last night I was talking with someone about the pros and cons of various programming languages and frameworks for data analysis. One of the pros of Python is its elegance. The primary con is that it can be slow.

The conversation reminded me of an apocryphal exchange between Winston Churchill and Bessie Braddock.

Braddock: Winston, you are drunk.

Churchill: Yes I am. And you, Bessie, are ugly. But I shall be sober in the morning, and you will still be ugly.

Python can be slow, though there are ways to improve its performance. But ugly code is just ugly, and there’s nothing you can do about it.

Python for data analysis

Posted on 24 October 2012 by John

I recommend using Python for data analysis, and I recommend Wes McKinney’s book Python for Data Analysis.

I prefer Python to R for mathematical computing because mathematical computing doesn’t exist in a vacuum; there’s always other stuff to do. I find doing mathematical programming in a general-purpose language is easier than doing general-purpose programming in a mathematical language. Also, general-purpose languages like Python have larger user bases, are better designed, have better tool support, etc.

Python per se doesn’t have everything you need for mathematical computing. You need to combine several tools and libraries, typically at least SciPy, matplotlib, and IPython. Because there are different pieces involved, it’s hard to find one source to explain using them all together. Also, even with the three additional components mentioned before, there is a need for additional software for working with structured data.

Wes McKinney developed the pandas library to give Python “rich data structures and functions designed to make working with structured data fast, easy, and expressive.” And now he has addressed the need for unified exposition by writing a single book that describes how to use the Python mathematical computing stack. Importantly, the book covers two recent developments that make Python more competitive with other environments for data analysis: enhancements to IPython and Wes’ own pandas project.

Python for Data Analysis is available for pre-order. I don’t know when the book will be available but Amazon lists the publication date as October 29. My review copy was a PDF, but at least one paper copy has been spotted in the wild:

Wes McKinney holding his book at O’Reilly’s Strata Conference. Photo posted on Twitter yesterday.

Computing log gamma differences

Posted on 14 July 2012 by John

Statistical computing often involves working with ratios of factorials. These factorials are often too big to fit in a floating point number, and so we work with logarithms. So if we need to compute log(a! / b!), we call software that calculates log(a!) and log(b!) directly without computing a! or b! first. More on that here. But sometimes this doesn’t work.

Suppose a = 10^40 and b = a − 10^10. Our first problem is that we cannot even compute b directly. Since a − b is 30 orders of magnitude smaller than a, we’d need about 100 bits of precision to begin to tell a and b apart, about twice as much as a standard floating point number. (Why 100? That’s the log base 2 of 10^30. And how much precision does a floating point number have? See here.)

Our next problem is that even if we could accurately compute b, the log gamma function is going to be approximately the same for a and b, and so the difference will be highly inaccurate.

So what do we do? We could use some sort of extended precision package, but that is not necessary. There’s an elegant solution using ordinary precision.

Let f(x) = log(Γ(x)). The mean value theorem says that

f(a + 1) − f(b + 1) = (a − b) f‘(c + 1)

for some c between a+1 and b+1. We don’t need to compute b, only a − b, which we know is 10^10. The derivative of the log of the gamma function is called the digamma function, written ψ(x). So

log(a! / b!) = 10^10 ψ(c+1).

But what is c? The mean value theorem only says that the equation above is true for some c. What c do we use? It doesn’t matter. Since a and b are so relatively close, the digamma function will take on essentially the same value for any value between a+1 and b+1. Therefore

log(a! / b!) ≈ 10^10 ψ(a).

We could compute this in two lines of Python:

from scipy.special import digamma
print 1e10*digamma(1e40)

Using SciPy with IronPython

Posted on 21 May 2012 by John

Three years ago I wrote a post about my disappointment using SciPy with IronPython. A lot has changed since then, so I thought I’d write a short follow-up post.

To install NumPy and SciPy for use with IronPython, follow the instructions here. [Update: no longer available.] After installation, NumPy works as expected.

There is one small gotcha with SciPy. To use SciPy with IronPython, start ipy with the command line argument -X:Frames. Then you can use SciPy as you would from CPython. For example.

c:> ipy -X:Frames
>>> import scipy as sp
>>> sp.pi
3.141592653589793

Without the -X:Frames option you’ll get an error when you try to import scipy.

AttributeError: 'module' object has no attribute '_getframe'

According to this page [link rot],

The issue is that SciPy makes use of the CPython API for inspecting the current stack frame which IronPython doesn’t enable by default because of a small runtime performance hit. You can turn on this functionality by passing the command line argument “-X:Frames” to on the command line.

More numerical analysis posts