Month: July 2008

Multiple string types: BSTR, wchar_t, etc.

Posted on by John

This morning I listened to a podcast interview with Kate Gregory. She used some terms I hadn’t heard in years: BSTR, OLE strings, etc.

Around a decade ago I was working with COM in C++ and had to deal with the menagerie of string types Kate Gregory mentioned. I wrote an article to get all the various types straight in my head: all the different memory allocation rules, conventions for use, conversions between types, etc. I never published the article. When I started my personal website I thought about posting the article there, but then I thought that by now nobody cared about such things. But the interview I listened to this morning made me think more people might be interested than I’d thought. So I posted my article Unravelling Strings in Visual C++ in case someone finds it useful.

Including images in LaTeX files

Posted on by John

Here are the rules for including images in LaTeX files as far as I can tell.

Near the top of your document, use \usepackage{graphicx} to load the graphicx package. Then at the point where you want to include your image, use \includeimage{...} where … is the path to your file.

If you want to create a PDF file with pdflatex, your image must be in PDF, PNG, or JPEG format.

If you want to create a DVI file with latex or a PS file with dvips, your image must be in PS or EPS format.

There’s no way to include a GIF file without first converting it to another file format.

If you use \usepackage{pgf} rather than  \usepackage{graphics} at the top of the file, nothing changes except that you must chop the file extensions off image file names.

Related post: Watch what you name graphics files in LaTeX

LaTeX and PowerPoint presentations

Posted on by John

I use LaTeX for math documents and PowerPoint for presentations. When I need to make a math presentation, I can’t have everything I want in one environment. I usually go with PowerPoint.

Yesterday I tried the LaTeX Beamer package based on a friend’s recommendation. I believe I’ll switch to using this package as my default for math presentations. Here are my notes on my experience with Beamer.

Installation

Beamer is available from SourceForge. The installation instructions begin by saying “Put all files somewhere where TeX can find them.” This made me think Beamer would be another undocumented software package, but just a few words later the instructions point to a 224-page PDF manual with plenty of detail. However, I would recommend a couple minor corrections to the documentation.

  1. The manual says that if you want to install Beamer under MiKTeX, use the update wizard. But the update wizard will only update packages already installed. To install new packages with MiKTeX, use the Package Manager. (Command line mpm.exe or GUI mpm_mfc.exe.)
  2. The manual says to install latex-beamer, pgf, and xcolor. The Package Manager shows no latex-beamer package, but does show a beamer package.

The installation went smoothly overall. However, the MiKTeX Package Manager doesn’t let you know when packages have finished installing. You just have to assume when it quits giving new messages that it must be finished. At least that was my experience using the graphical version.

Using Beamer

I found Bruce Byfield’s introduction to Beamer helpful. The Beamer package is simple to use and well documented.

It’s nice to use real math typography rather than using PowerPoint hacks or pasting in LaTeX output as images. I also like animating bullet points simply by adding pause to the end of an enumerated item.

Inserting images

The biggest advantage that PowerPoint has over LaTeX is working with images. With PowerPoint you can:

  1. Paste images directly into your presentations.
  2. Edit files in place.
  3. Carry around your entire presentation as a single file.
  4. Include multiple image formats in a consistent way.

The last point may not seem like much until you’ve tried to figure out how to include images in LaTeX.

Visualizing software development effort

Posted on by John

Thomas Guest posted a great article today called Distorted Software [link went away] that, among other things, points out the problem with software diagrams with big boxes and little arrows:

big boxes, little arrows

Most of the work will go into making the connections work.  In other words, the bulk of the work is in the little arrows, not the big boxes. He suggests a better diagram might look like this:

big arrows, little boxes

Michael Brecker

Posted on by John

When I was in college, my saxophone teacher recommended I study Michael Brecker. I enjoyed his music, especially his recordings with Steps Ahead, but for some reason I quit listening to Brecker sometime after college. Then earlier this year I bought Brecker’s last album Pilgrimage after reading a glowing review.

Brecker recorded Pilgrimage as he was dying of leukemia, but there’s nothing morbid about the album. It’s upbeat, complex, and beautiful. Brecker spent his final days pursuing his art surrounded by friends.

Unit test boundaries

Posted on by John

Phil Haack has a great article on unit test boundaries. A unit test must not touch the file system, interact with a database, or communicate across a network. Tests that break these rules are necessary, but they’re not unit tests. With some hard thought, the code with external interactions can be isolated and reduced. This applies to both production and test code

As with most practices related to test-driven development, the primary benefit of unit test boundaries is the improvement in the design of the code being tested. If your unit test boundaries are hard to enforce, your production code may have architectural boundary problems. Refactoring the production code to make it easier to test will make the code better.

Three ways of tuning an adaptively randomized trial

Posted on by John

Yesterday I gave a presentation on designing clinical trials using adaptive randomization software developed at M. D. Anderson Cancer Center. The heart of the presentation is summarized in the following diagram.

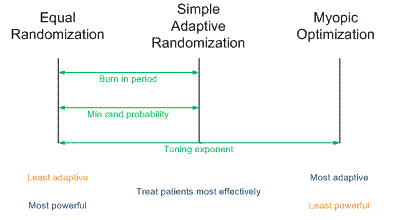
Diagram of three methods of tuning adaptively randomized trial designs

(A slightly larger and clearer version if the diagram is available here.)

Traditional randomized trials use equal randomization (ER). In a two-arm trial, each treatment is given with probability 1/2. Simple adaptive randomization (SAR) calculates the probability that a treatment is the better treatment given the data seen so far and randomizes to that treatment with that probability. For example, if it looks like there’s an 80% chance that Treatment B is better, patients will be randomized to Treatment B with probability 0.80. Myopic optimization (MO) gives each patient what appears to be the best treatment given the available data with no randomization.

Myopic optimization is ethically appealing, but has terrible statistical properties. Equal randomization has good statistical properties, but will put the same number of patients on each treatment, regardless of the evidence that one treatment is better. Simple adaptive randomization is a compromise position, retaining much of the power of equal randomization while also treating more patients on the better treatment on average.

The adaptive randomization software provides three ways of compromising between the operating characteristics ER and SAR.

  1. Begin the trial with a burn-in period of equal randomization followed by simple adaptive randomization.
  2. Use simple adaptive randomization, except if the randomization probability drops below a certain threshold, substitute that minimum value.
  3. Raise the simple adaptive randomization probability to a power between 0 and 1 to obtain a new randomization probability.

Each of these three approaches reduces to ER at one extreme and SAR at the other. In between the extremes, each produces a design with operating characteristics somewhere between those of ER and SAR.

In the first approach, if the burn-in period is the entire trial, you simply have an ER trial. If there is no burn-in period, you have an SAR trial. In between you could have a burn-in period equal to some percentage of the total trial between 0 and 100%. A burn-in period of 20% is typical.

In the second approach, you could specify the minimum randomization probability as 0.5, negating the adaptive randomization and yielding ER. At the other extreme, you could set the minimum randomization probability to 0, yielding SAR. In between you could specify some non-zero randomization probability such as 0.10.

In the third approach, a power of zero yields ER. A power of 1 yields SAR. Unlike the other two approaches, this approach could yield designs approaching MO by using powers larger than 1. This is the most general approach since it can produce a continuum of designs with characteristics ranging from ER to MO. For more on this approach, see Understanding the exponential tuning parameter in adaptively randomized trials.

So with three methods to choose from, which one do you use? I did some simulations to address this question. I expected that all three methods would perform about the same. However, this is not what I found. To read more, see Comparing methods of tuning adaptive randomized trials.

Update: The ideas in this post and the technical report mentioned above have been further developed in this paper.

Related: Adaptive clinical trial design

Why so few electronic medical records

Posted on by John

Computerworld has a good article on why electronic medical records are so slow to appear. Many people I’ve talked to believe that medical data is just harder to work with than other kinds of data. They see the barriers to electronic medical records as primarily technical. That’s hard to swallow when nearly every other sector of the economy has electronic records. As the Computerworld article says, we’ve had the technology to pull this off for 30 years. There are more plausible economic explanations for why EMRs are uncommon. In a nutshell, the party that pays to develop an EMR is not the party that reaps most of the financial benefit so there’s little incentive to move forward.

Outlook hack: fixing useless subject lines

Posted on by John

John Udell pointed out today that Microsoft Outlook lets you edit the subject line on mail you’ve received, changing it to the subject line you wish the sender had used. So rather than maintaining a mental dictionary mapping irrelevant email subject lines to what they mean to you, you could just edit the subject line.