Suppose you’ve learned a thousand of something, maybe a thousand kanji or a thousand chemicals or a thousand species of beetles. Now you want to review them to retain what you’ve learned.
Now suppose you have a program to quiz you, drawing items from your list at random with replacement. Say you draw 100 items a day. How long until you’ve seen everything at least once?
A naive estimate would be 10 days, but that assumes you never draw the same item twice in 1000 draws. According to the birthday problem principle, there’s a 50-50 chance you’ll see a duplicate by the time you’ve made √1000 ≈ 32 draws. Drawing 100 cards a day, you’ll likely see duplicates the first day.
Coupon collector problem
Random sampling with replacement is not an efficient way to exhaustively sample a large population. The coupon collector problem says that for a set of N items, the expected number of draws before you’ve seen everything once is approximately
N(log N + γ)
for large N. Here γ is Euler’s constant. When N = 1000 this works out to 7485. So if you draw 100 items a day, you’d expect to have seen everything after 75 days. Of course it might take more or less time than that, but that’s the average.
To put it another way, random sampling with replacement is about 7.5 times less efficient than systematic sampling if you’re concerned with expected time to exhaustive sampling.
In general, the relative inefficiency is log N + γ. So for a set of N = 100 things, for example, the relative inefficiency is about 5.2.
Occupancy problem
We can arrive at approximately the same result using methods from a couple other posts. Last week I wrote about the occupancy problem distribution. That post defined X(N, r) and gives its mean and variance.
When we draw r random samples with replacement from a set of N items, let X(N, r) be the random variable that represents the number of distinct items in the sample. …
The mean of X(N, r) is

So if we have set of N = 1000 things and sample with replacement 7000 times, we expect to see 999 distinct items on average. Of course this is an average, so we might see less. And we might see more, but not much more!
Probabilities
The approaches above have worked with expected values, not individual probabilities. The coupon collector problem looks at the expected number of draws needed to before you see everything. The occupancy problem looks at the expected number of things you’ve seen after a certain number of draws.
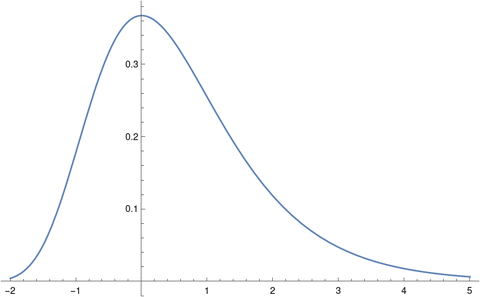
We could calculate the probability of having seen everything after r draws using the expression here.
After 7,000 draws, there’s a 40% chance we’ve seen everything. After 7,274 draws the chances of having seen everything are even, i.e. the median number of draws is 7,274, not that different from the mean number of draws estimated above.
After 10,000 draws there is a 96% chance we’ve seen everything.
For more on the distribution of the number of draws necessary, see the follow-on post Collecting a large number of coupons.
A note on computation
The expression used in the previous section relies on Stirling numbers, and these are a bit difficult to compute. The calculation involves very large integers, but we cannot use logarithms because we are adding large numbers, not multiplying them.
This post includes Python code for calculating Stirling numbers using Python’s large integer feature. But the probability we’re after is the ratio of two integers too large to convert to floating point numbers. The following code gets around this problem using the Decimal class.
from math import comb, log10
from decimal import Decimal, getcontext
def k_factorial_stirling(n, k):
return sum((-1)**i * comb(k, i)*(k-i)**n for i in range(k+1))
def prob(N, r):
getcontext().prec = int(r*log10(N)) + 100
return Decimal( k_factorial_stirling(r, N) ) / Decimal( N**r)
print( round(prob(1000, 7000), 4) )
print( round(prob(1000, 7274), 4) )
print( round(prob(1000, 10000), 4) )
How do we know how many decimal places we’ll need? We’re computing a probability, so the denominator is larger than the numerator. We estimate the number of digits in the denominator, then throw in 100 more just for good measure.

![\[ \frac{\binom{{\color{red} n_1}}{k}\binom{n-{\color{red} n_1}}{{\color{blue} r}-k}} {\binom{n}{{\color{blue}r}}} = \frac{\binom{{\color{blue} r}}{k} \binom{n-{\color{blue} r}}{{\color{red} n_1} - k}} { \binom{n}{{\color{red} n_1}} } \]](https://www.johndcook.com/hypergeometric_symmetry.png)