Here’s a post from the blog Continuous everywhere but differentiable nowhere that explains some of the math that was used to design China’s water cube stadium.
I found this blog via Carnival of Mathematics #39.
Month: August 2008
Medieval software project management
Centuries ago, English communities would walk the little boys around the perimeter of their parish as a way of preserving land records. This was called “beating the bounds.” The idea was that by teaching the boundaries to someone young, the knowledge would be preserved for the lifespan of that person. Of course modern geological survey techniques make beating the bounds unnecessary.
Software development hasn’t reached the sophistication of geographic survey. Many software shops use a knowledge management system remarkably similar to beating the bounds. They hire a new developer to work on a new project. That developer will remain tied to that project for the rest of his or her career, like a serf tied to the land. The knowledge essential to maintaining that project resides only in the brain of its developer. There are no useful written records or reliable maps, just like medieval property boundaries.
Who do you call when SOA software breaks?
The idea behind SOA (service-oriented architecture) is that instead of developing monolithic applications, businesses should build “services,” typically web services, that do specific tasks. These services can then be combined in all kinds of useful ways.
This is not a new idea but the latest step in a progression of similar ideas. First subroutines, then libraries, then objects, then components, and now services. Each step offers better encapsulation than its predecessor and comes closer to delivering on the promise of making it possible to assemble software out of modular pieces.
There are challenges to making all this work, and they are not primarily technical challenges. As Gerald Weinberg says, “it’s always a people problem.”
If different groups are publishing services that combine to make the software someone uses, who do they call when something breaks? This is not an insurmountable problem, but it’s not trivial either. When someone can’t get their work done because software isn’t working and they call you for help, it’s hard to tell them that you just provide a “service” and that someone else is responsible for their problem. You may be telling them the truth, but it sounds like a run-around.
When you provide a service that another group uses, how do you make sure they understand how to use it correctly? Software can verify that the correct data types come in: this field should be a number, this one text between 5 and 12 characters long, etc. But software doesn’t assure that the caller understands what they should be passing your service to get back what they really want. This too is a people problem.
How do you keep track of all the services you depend on? Who is responsible for monitoring them?
Using third-party commercial services is probably simpler than using a service developed in a different part of your own company. With commercial service providers, there are contracts (technical and legal) with service level agreements. And since money changes hands, companies have structures in place to monitor such things. But when you’re using software developed by your counterpart three floors up in another department, there’s probably not as much infrastructure in place. And if there is, it’s easier to circumvent.
These problems all go under the heading of SOA governance. It’s useful to give complex things a name, but doing so can obscure complexity. You can’t make the problems go away by forming a SOA governance committee.
Random inequalities V: beta distributions
I’ve put a lot of effort into writing software for evaluating random inequality probabilities with beta distributions because such inequalities come up quite often in application. For example, beta inequalities are at the heart of the Thall-Simon method for monitoring single-arm trials and adaptively randomized trials with binary endpoints.
It’s not easy to evaluate P(X > Y) accurately and efficiently when X and Y are independent random variables. I’ve seen several attempts that were either inaccurate or slow, including a few attempts on my part. Efficiency is important because this calculation is often in the inner loop of a simulation study. Part of the difficulty is that the calculation depends on four parameters and no single algorithm will work well for all parameter combinations.
Let g(a, b, c, d) equal P(X > Y) where X ~ beta(a, b) and Y ~ beta(c, d). Then the function g has several symmetries.
- g(a, b, c, d) = 1 – g(c, d, a, b)
- g(a, b, c, d) = g(d, c, b, a)
- g(a, b, c, d) = g(d, b, c, a)
The first two relations were published by W. R. Thompson in 1933, but as far as I know the third relation first appeared in this technical report in 2003.
For special values of the parameters, the function g(a, b, c, d) can be computed in closed form. Some of these special cases are when
- one of the four parameters is an integer
- a + b + c + d = 1
- a + b = c + d = 1.
The function g(a, b, c, d) also satisfies several recurrence relations that make it possible to bootstrap the latter two special cases into more results. Define the beta function B(a, b) as Γ(a, b)/(Γ(a) Γ(b)) and define h(a, b, c, d) as B(a+c, b+d)/( B(a, b) B(c, d) ). Then the following recurrence relations hold.
- g(a+1, b, c, d) = g(a, b, c, d) + h(a, b, c, d)/a
- g(a, b+1, c, d) = g(a, b, c, d) – h(a, b, c, d)/b
- g(a, b, c+1, d) = g(a, b, c, d) – h(a, b, c, d)/c
- g(a, b, c, d+1) = g(a, b, c, d) + h(a, b, c, d)/d
For more information about beta inequalities, see these papers:
Previous posts on random inequalities:
Statistically significant but incorrect
The Decision Science News blog [link died] has an article highlighting a tool to illustrate how often experiments with significant p-values draw false conclusions. Here’s the website they refer to.
Entering Unicode characters in Linux
I ran across this post from Aaron Toponce explaining how to enter Unicode characters in Linux applications. Hold down the shift and control keys while typing “u” and the hex values of the Unicode character you wish to enter. I tried this and it worked in Firefox, GEdit, and Gnome Terminal, but not in OpenOffice. I was running Ubuntu 7.10.
Three ways to enter Unicode characters in Windows
Here are three approaches to entering Unicode characters in Windows. See the next post for entering Unicode characters in Linux.
Alt – x
In Microsoft Word you can insert Unicode characters by typing the hex value of the character then typing Alt-x. You can also see the Unicode value of a character by placing the cursor immediately after the character and pressing Alt-x. This also works in applications that use the Windows rich edit control such as WordPad and Outlook.
Pros: Nothing to install or configure. You can see the numeric value before you turn it into a symbol. It’s handy to be able to go the opposite direction, looking up Unicode values for characters.
Cons: Does not work with many applications.
Alt – +
Another approach which works with more applications is as follows. First create a registry key under HKEY_CURRENT_USER of type REG_SZ called EnableHexNumpad, set its value to 1, and reboot. Then you can enter Unicode symbols by holding down the Alt key and typing the plus sign on the numeric keypad followed by the character value. When you release the Alt key, the symbol will appear. This approach worked with most applications I tried, including Firefox and Safari, but did not with Internet Explorer.
Pros: Works with many applications. No software to install.
Cons: Requires a registry edit and a reboot. It’s awkward to hold down the Alt key while typing several other keys. You cannot see the numbers you’re typing. Doesn’t work with every application.
UnicodeInput
Another option is to install the UnicodeInput utility. This worked with every application I tried, including Internet Explorer. Once installed, the window below pops up whenever you hold down the Alt key and type the plus sign on the numeric keypad. Type the numeric value of the character in the box, click the Send button, and the character will be inserted into the window that had focus when you clicked Alt-plus.
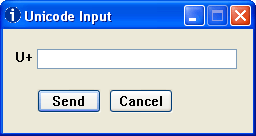
Pros: Works everywhere (as far as I’ve tried). The software is free. Easy to use.
Cons: Requires installing software.
Related links
Improved PowerShell prompt
A while back I wrote a post on how to customize your PowerShell prompt. Last week Tomas Restrepo posted an article on a PowerShell prompt that adds color and shortens the path in a more subtle way. I haven’t tried it out yet, but his prompt looks much better than what I’ve been using.
If you’re a long-time Windows user you might be worried that all this PowerShell stuff is starting to look a lot like Unix. Well, it is. Some of the folks on the PowerShell team have a Unix background and they’re bringing some of the best of Unix to Windows. The Unix world has more experience operating from the command line and so it’s wise to learn from them.
On the other hand, PowerShell is emphatically not bash for Windows. PowerShell is thoroughly object oriented and in that respect unlike any Unix shell. Also, PowerShell is strongly tied to Microsoft libraries, particularly .NET but also COM and WMI.
Applying PageRank algorithm to biology
Scientific American’s 60 Second Science has a podcast Google-style rankings for ecosystems reporting on a presentation by Stefano Allesino suggesting applying a Google-like algorithm to determine conservation priorities. Just as web pages rank higher when many other pages link to them, and organism would be a higher priority for conservation efforts if it is part of the food chain for many other organisms.
The Holy Grail of CSS
Basic tasks are simple in CSS, but even slightly harder tasks can be incredibly difficult. Controlling fonts, margins, and so forth is a piece of cake. But controlling page layout is another matter. In his book Refactoring HTML, Elliotte Rusty Harold describes a technique as
so tricky that it took any smart people quite a few years of experimentation to develop the technique show here. In fact, so many people searched for this while believing that it didn’t actually exist that this technique goes under the name “The Holy Grail.”
What is the incredibly difficult task that took so many years to discover? Teaching a web browser to play chess using only style sheets? No, three column layout. I kid you not. He goes on to say
The goal is simple: two fixed-width columns on the left and the right and a liquid center for the content in the middle. (That something so frequently needed was so hard to invent doesn’t speak well of CSS as a language, but it s the language we have to work with.)
You can read more about the Holy Grail of CSS in an article by Matthew Levine.
I appreciate the advantages of CSS, though I do wish it didn’t have such a hockey stick learning curve. I’ve heard people say not to bother learning overly difficult technologies because if you find it too difficult, so will everyone else and it will die off. But CSS seems to be firmly established with no competitor.