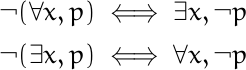
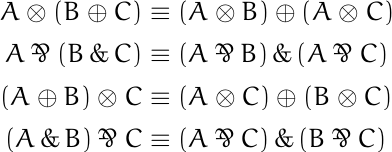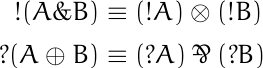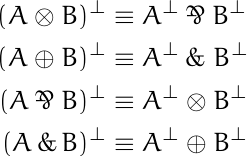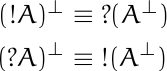Axioms in modal logic often say that one sequence of boxes and diamonds in front of a proposition p implies another sequence of boxes and diamonds in front of p. For example, Axiom 4 says
□ p → □□ p
and Axiom 5 says
◇p → □◇p.
Every axiom has a dual form. The dual form of Axiom 4 is
◇◇p → ◇p
and the dual of Axiom 5 is
◇□ p → □ p.
Computing duals
There’s a simple way to compute the dual of such axioms:
Rotate all the squares 45° and rotate the arrow 180°.
This turns boxes into diamonds, diamonds into boxes, and flips the direction of implication.
Shell and Perl
We could do this using the tr utility at the command line
$ echo '□□◇□◇p → □◇p' | tr '□◇→' '◇□←'
◇◇□◇□p ← ◇□p
We could also do the same thing in Perl, using its tr operator
$prop = "□□◇□◇p → □◇p";
($dual = $prop) =~ tr/□◇→/◇□←/;
print "$prop\n$dual\n";
This prints
□□◇□◇p → □◇p
◇◇□◇□p ← ◇□p
It’s important to note that tr in both its incarnations does simultaneous replacement. It did what we expected, so it might be hard to notice.
tr takes two strings of the same length as arguments. Call the first one from and the second to. The easiest way to implement tr would have been to replace the first character of from with the first character of to, then replace the second character of from with the second character of to, etc.
This would have turned all our boxes into diamonds, then turned all diamonds into boxes, and so we’d be left with nothing but boxes! Our sequence □□◇□◇ would have turned into □□□□□.
Proof
Why is the rule above valid?
Let ○ stand for either a box or a diamond and suppose we start with
○1 ○2 … ○m p → ○m+1 ○m+2 … ○n p
where p is an arbitrary proposition.
Now let ○’ stand for the dual of ○. So if ○ is a box, ○’ is a diamond, and vice versa. Then
○ p = ¬○’ ¬p
by definition. (If you take □ as primary, then the equation above is the definition of ◇. If you take ◇ as primary, it’s the definition of □.) Apply this rule everywhere.
¬○’1 ¬¬○’2 ¬… ¬○’m ¬p → ¬○’m+1 ¬¬○’m+2 … ¬○’n ¬p
Now cancel out all the pairs of consecutive negations.
¬○’1 ○’2 … ○’m ¬p → ¬○’m+1 ○’m+2 … ○’n ¬p
Now take the contrapositive: (¬P → ¬Q) → (Q → P).
○’m+1 ○’m+2 … ○’n ¬p → ○’1 ○’2 … ○’m ¬p
Since p was an arbitrary proposition, we can replace p with ¬p.
○’m+1 ○’m+2 … ○’n p → ○’1 ○’2 … ○’m p
What we have above is the proposition we started with, with all the boxes replaced with diamonds, all the diamonds replaced with boxes, and the direction of the implication reversed.
More modalities
Notice that the theorem and proof still holds if there are multiple modalities. Suppose we have a set of modalities Ki. You could interpret
Ki p
as saying the ith agent knows proposition p is true. Then the dual is defined by
K’i p = ¬ Ki ¬ p,
which could be interpreted as saying the ith agent does not know p to be false.
You could form the dual of a proposition involving K and K‘ expressions by adding primes to terms that don’t have them, and removing primes from terms that do, and turning the implication around. The proof would be the same as above, only we don’t restrict ○ to being □ or ◇.


![\begin{table}[] \begin{tabular}{lccll} & \phantom{i}add\phantom{i} & mult & & \\ \cline{2-3} \multicolumn{1}{l|}{conjunction} & \multicolumn{1}{c|}{\&} & \multicolumn{1}{c|}{\otimes} & & \\ \cline{2-3} \multicolumn{1}{r|}{disjunction} & \multicolumn{1}{c|}{\oplus} & \multicolumn{1}{c|}{\parr} & & \\ \cline{2-3} & & & & \end{tabular} \end{table}](https://www.johndcook.com/linear_con_dis_add_mult.png)
![\begin{table}[] \begin{tabular}{lcccl} & add & mult & exp & \\ \cline{2-4} \multicolumn{1}{r|}{positive} & \multicolumn{1}{c|}{\oplus} & \multicolumn{1}{c|}{\otimes} & \multicolumn{1}{c|}{!} & \\ \cline{2-4} \multicolumn{1}{r|}{negative} & \multicolumn{1}{c|}{\&} & \multicolumn{1}{c|}{\parr} & \multicolumn{1}{c|}{?} & \\ \cline{2-4} \end{tabular} \end{table}](https://www.johndcook.com/linear_pos_neg_add_mult_exp.png)