Bessel zero spacing

Posted on 31 January 2024 by John

Bessel functions are to polar coordinates what sines and cosines are to rectangular coordinates. This is why Bessel function often arise in applications with radial symmetry.

The locations of the zeros of Bessel functions are important in application, and so you can find software for computing these zeros in mathematical libraries. In days gone by you could find them in printed tables, such as Table 9.5 in A&S.

Bessel functions are solutions to Bessel’s differential equation,

$x^2 y'' + x y' + (x^2 - \nu^2) y = 0$

For each ν the functions J_ν and Y_ν, known as the Bessel functions of the first and second kind respectively, form a basis for the solutions to Bessel’s equation. These functions are analogous to cosine and sine

As x → ∞, Bessel functions asymptotically behave like damped sinusoidal waves. Specifically,

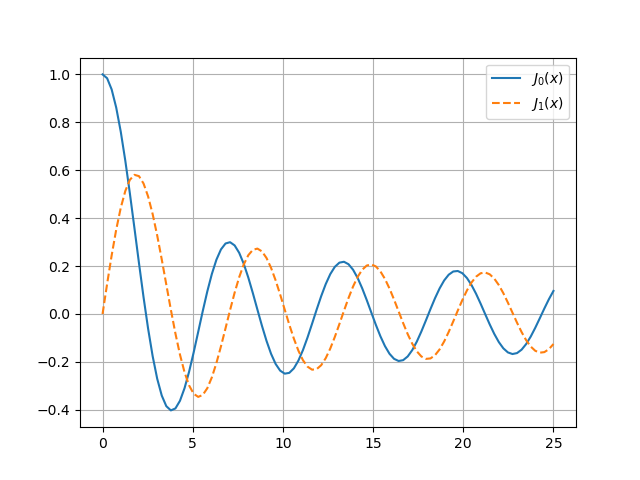
$\begin{align*} J_\nu(x) &\sim \sqrt{\frac{2}{\pi x}} \cos(x - \pi\nu/2 - \pi/4) \\ Y_\nu(x) &\sim \sqrt{\frac{2}{\pi x}} \sin(x - \pi\nu/2 - \pi/4) \end{align*}$

So if for large x Bessel functions of order ν behave something like sin(x), you’d expect the spacing between the zeros of the Bessel functions to approach π, and this is indeed the case.

We can say more. If ν² > ¼ then the spacing between zeros decreases toward π, and if ν² < ¼ the spacing between zeros increases toward π. This is not just true of J_ν and Y_ν but also of their linear combinations, i.e. to any solution of Bessel’s equation with parameter ν.

If you look carefully, you can see this in the plots of J₀ and J₁ below. The solid blue curve, the plot of J₀, crosses the x-axis at points closer together than π, and dashed orange curve, the plot of J₁, crosses the x-axis at points further apart than π.

For more on the spacing of Bessel zeros see [1].

[1] F. T. Metcalf and Milos Zlamal. On the Zeros of Solutions to Bessel’s Equation. The American Mathematical Monthly, Vol. 73, No. 7, pp. 746–749

Coloring the queen’s graph

Posted on 30 January 2024 by John

Suppose we have an n × n chessboard. The case n = 8 is of course most common, but we consider all positive integer values of n.

The graph of a chess piece has an edge between two squares if and only if the piece can legally move between the two squares.

Now suppose we have a rule that if a piece can move between two squares, the squares must be colored differently. The minimum number of colors necessary to color the chessboard this was is the chromatic number of that piece’s graph.

The chromatic number of a rook is clearly at least n: since a rook can move between any two squares in a row, every square in the row must be a different color. And in fact the chromatic number for a rook’s graph is exactly n.

Bishops are a little more complicated. If n is even, then the chromatic number for a bishop is n. If n is odd, the number is n for a white bishop but n − 1 for a black bishop. Thinking of a 3 × 3 board shows why the two bishops are different.

Now a queen is sorta like a rook and a bishop combined, but determining the chromatic number for a queen’s graph is more difficult. The chromatic number of a queen can be no less than that of a rook since the former can make all the moves of the latter. So the queen’s chromatic number is at least n, but is it equal to n?

The results stated above can be found in [1].

Let k(n) be the chromatic number of a queen’s graph on an the n × n chessboard. The results in [1] regarding k(n) are summarized as follows.

k(1) = 1
k(2) = 4
k(3) = k(4) = 5
k(6) = 7
k(n) = n if n is not divisible by 2 or 3.

The authors stated that they had found an example proving that k(8) ≤ 9 and conjectured that k(8) = 9. You can find a C++ program that confirms this conjecture here.

The authors conjectured that k(n) ≤ n + 1 for all n > 3. I don’t know whether this has been proven. My impression following a brief search is that the problem of finding k(n) for all n is still not fully resolved.

Update: According to a link in the comments, n = 27 is the smallest n such that k(n) is unknown.

[1] M. R. Iyer and V. V. Menon. On Coloring the n × n Chessboard. The American Mathematical Monthly, 1966, Vol. 73, pp. 721–725.

When is a function of two variables separable?

Posted on 18 January 2024 by John

Given a function f(x, y), how can you tell whether f can be factored into the product of a function g(x) of x alone and a function h(y) of y alone? Depending on how an expression for f is written, it may or may not be obvious whether f(x, y) can be separated into g(x) h(y).

There are several situations in which you might want to know whether a function is separable. For example, the ordinary differential equation

y′ = f(x, y)

can be solved easily when f(x, y) = g(x) h(y).

You might want to do something similar for a partial differential equation, using separation of variables, possibly choosing a coordinate system that allows the separation of variables trick to work.

Aside from applications to differential equations, you might want to know whether a polynomial in two variables can be factored into the product of polynomials in each variable separately.

In [1] David Scott gives a simple necessary condition for f to be separable:

f f_xy = f_x f_y

Here the subscripts indicate partial derivatives.

It’s easy to see this condition is necessary. Scott shows the condition is also sufficient under some mild technical assumptions.

As an example, determine the value of k such that the differential equation

y′ = 6xy² + 3y² −4x + k

is separable.

Scott’s equation

f f_xy = f_x f_y

becomes

(6xy² + 3y² −4x + k)(12y) = (6y² −4)(12xy + 6y)

which holds if and only if k = −2.

[1] David Scott. When is an Ordinary Differential Equation Separable? The American Mathematical Monthly, Vol. 92, No. 6, pp. 422–423

Applications of Bernoulli differential equations

Posted on 17 January 2024 by John

When a nonlinear first order ordinary differential equation has the form

$\frac{dy}{dx} + P(x)\,y = Q(x)\, y^n$

with n ≠ 1, the change of variables

$u = y^{1-n}$

turns the equation into a linear equation in u. The equation is known as Bernoulli’s equation, though Leibniz came up with the same technique. Apparently the history is complicated [1].

It’s nice that Bernoulli’s equation can be solve in closed form, but is it good for anything? Other than doing homework in a differential equations course, is there any reason you’d want to solve Bernoulli’s equation?

Why yes, yes there is. According to [1], Bernoulli’s equation is a generalization of a class of differential equations that came out of geometric problems.

Someone asked about applications of Bernoulli’s equation on Stack Exchange and got a couple interesting answers.

The first answer said that a Bernoulli equation with n = 3 comes up in modeling frictional forces. See also this post on drag forces.

The second answer links to a paper on Bernoulli memristors.

[1] Adam E. Parker. Who Solved the Bernoulli Differential Equation and How Did They Do It? College Mathematics Journal, vol. 44, no. 2, March 2013.

The IQ Test That AI Can’t Pass

Posted on 16 January 2024 by Wayne Joubert

Large language models have recently achieved remarkable test scores on well-known academic and professional exams (see, e.g., [1], p. 6). On such tests, these models are at times said to reach human-level performance. However, there is one test that humans can pass but every AI method known to have been tried has abysmally failed.

The Abstraction and Reasoning Corpus (ARC) benchmark [2] was developed by François Chollet to measure intelligence in performing tasks never or rarely seen before. We all do tasks something like this every day, like making a complicated phone call to correct a mailing address. The test is composed of image completion problems similar to Raven’s Progressive Matrices but more complex. Given images A, B and C, one must identify the image D such that the relationship “A is to B as C is to D” holds. Sometimes several examples of the A:B relationship are given.

The problem is hard because the relationship patterns between A and B that humans could easily identify (for example, image shrinking, rotating, folding, recoloring, etc.) might be many, many different things—more than can easily be trained for. By construction, every problem is qualitatively, unpredictably different, so the common approach of training on the training set doesn’t work. Instead, bonafide reasoning on a new kind of problem for each case is required.

Several competitions with prize money have encouraged progress on the ARC benchmark [3]. In these, each entrant’s algorithm must be tested against an unseen ARC holdout set. The leaderboard for the ARCathon 2023 challenge completed last month shows top score of 30 percent [4]; this is excellent progress on a very hard problem, but far from a perfect score or anything else resembling passing.

Ilya Sutskever has famously warned we shouldn’t bet against deep learning, and perhaps a future LLM will do much better on this benchmark. Others feel a new approach is needed, for example, from the burgeoning field of neurosymbolic methods. In any case, these results show at the present moment in this rapidly progressing field, we don’t seem to be anywhere close to strong forms of AGI, artificial general intelligence.

[1] OpenAI, “GPT-4 Technical Report,” https://cdn.openai.com/papers/gpt-4.pdf

[2] François Chollet, “On the Measure of Intelligence,” https://arxiv.org/abs/1911.01547

[3] “Abstraction and Reasoning Challenge,” https://www.kaggle.com/c/abstraction-and-reasoning-challenge

[4] “Winners – Lab42, “https://lab42.global/past-challenges/arcathon-2023/“

Means of means bounding the logarithmic mean

Posted on 16 January 2024 by John

The geometric, logarithmic, and arithmetic means of a and b are defined as follows.

$\begin{align*} G &= \sqrt{ab} \\ L &= \frac{b - a}{\log b - \log a} \\ A &= \frac{a + b}{2} \end{align*}$

A few days ago I mentioned that G ≤ L ≤ A. The logarithmic mean slips between the geometric and arithmetic means.

Or to put it another way, the logarithmic mean is bounded by the geometric and arithmetic means. You can bound the logarithmic mean more tightly with a mixture of the geometric and arithmetic means.

In [1] the authors show that

$G^{2/3} A^{1/3} \leq L \leq \tfrac{2}{3}G + \tfrac{1}{3}A$

Note that the leftmost expression is the geometric mean of G, G, and A, and the rightmost expression is the arithmetic mean of G, G, and A. We can write this as

$G(G, G, A) \leq L \leq A(G, G, A)$

where G with no argument is the geometric mean of a and b and G with three arguments is the geometric mean of those arguments, and similarly for A.

The following plot shows how well these means of means bound the logarithmic mean. We let a = 1 and let b vary from 1 to 10o.

The upper bound is especially tight for moderate values of b. When I first made the plot I let b run up to 10 and there were apparently only four curves in the plot. I had to pick a larger value of b before the curves for L and (2G + A)/3 to be distinguished.

[1] Graham Jameson and Peter R. Mercer. The Logarithmic Mean Revisited. The American Mathematical Monthly, Vol. 126, No. 7, pp. 641-645

When zeros at natural numbers implies zero everywhere

Posted on 11 January 2024 by John

Suppose a function f(z) equals 0 at z = 0, 1, 2, 3, …. Under what circumstances might you be able to conclude that f is zero everywhere?

Clearly you need some hypothesis on f. For example, the function sin(πz) is zero at every integer but certainly not constantly zero.

Carlson’s theorem says that if f is analytic and bounded for z with non-negative real part, and equals zero at non-negative integers, then f is constantly zero.

Carlson’s theorem doesn’t apply to sin(πz) because this function is not bounded in the complex plane. It is bounded on the real axis, but that’s not enough. The identity

sin(z) = ( exp(iz) – exp(-iz) ) / 2i

shows that the sine function grows exponentially in the vertical direction.

Liouville’s theorem says that if a function is analytic and bounded everywhere then it must be constant. Carleson’s theorem does not require that the function f be bounded everywhere but in the right half-plane.

In fact, the boundedness requirement can be weakened to requiring f(z) be O( exp(k|z|) ) for some k < π. This, in combination with having zeros at 0, 1, 2, 3, …. is enough to conclude that f is zero.

Ky Fan’s inequality

Posted on 8 January 2024 by John

Let

$x = (x_1, x_2, x_3, \ldots, x_n)$

with each component satisfying 0 < x_i ≤ 1/2. Define the complement x′ by taking the complement of each entry.

$x' = (1 - x_1, 1 - x_2, 1 - x_3, \ldots, 1 - x_n)$

Let G and A represent the geometric and arithmetic mean respectively.

Then Ky Fan’s inequality says

$\frac{G(x)}{G(x')} \leq \frac{A(x)}{A(x')}$

Now let H be the harmonic mean. Since in general H ≤ G ≤ A, you might guess that Ky Fan’s inequality could be extended to

$\frac{H(x)}{H(x')} \leq \frac{G(x)}{G(x')} \leq \frac{A(x)}{A(x')}$

and indeed this is correct.

Source: Jósef Sándor. Theory and Means and Their Inequalities.

Integral representations of means

Posted on 6 January 2024 by John

The average of two numbers, a and b, can be written as the average of x over the interval [a, b]. This is easily verified as follows.

$\frac{1}{b-a}\int_a^b x\, dx = \frac{1}{b-a} \left( \frac{b^2}{2} - \frac{a^2}{2}\right) = \frac{a+b}{2}$

The average is the arithmetic mean. We can represent other means as above if we generalize the pattern to be

$\varphi^{-1}\left(\,\text{average of } \varphi(x) \text{ over } [a, b] \,\right )$

For the arithmetic mean, φ(x) = x.

Logarithmic mean

If we set φ(x) = 1/x we have

$\left(\frac{1}{b-a} \int_a^b x^{-1}\, dx \right)^{-1} = \left(\frac{\log b - \log a}{b - a} \right)^{-1} = \frac{b - a}{\log b - \log a}$

and the last expression is known as the logarithmic mean of a and b.

Geometric mean

If we set φ(x) = 1/x² we have

$\left(\frac{1}{b-a} \int_a^b x^{-2}\, dx \right)^{-1/2} = \left(\frac{1}{b-a}\left(\frac{1}{a} - \frac{1}{b} \right )\right)^{-1/2} = \sqrt{ab}$

which gives the geometric mean of a and b.

Identric mean

In light of the means above, it’s reasonable ask what happens if we set φ(x) = log x. When we do we get a more arcane mean, known as the identric mean.

The integral representation of the identric mean seems natural, but when we compute the integral we get something that looks arbitrary.

$\begin{align*} \exp\left( \frac{1}{b-a} \int_a^b \log x\, dx \right) &= \exp\left( \left.\frac{1}{b-a} (x \log x - x)\right|_a^b \right) \\ &= \exp\left( \frac{b \log b - a \log a - b + a}{b-a} \right) \\ &= \frac{1}{e} \left( \frac{b^b}{a^a} \right)^{1/(b-a)} \end{align*}$

The initial expression looks like something that might come up in application. The final expression looks artificial.

Because the latter is more compact, you’re likely to see the identric mean defined by this expression, then later you might see the integral representation. This is unfortunate since the integral representation makes more sense.

Order of means

It is well known that the geometric mean is no greater than the arithmetic mean. The logarithmic and identric means squeeze in between the geometric and arithmetic means.

If we denote the geometric, logarithmic, identric, and arithmetic means of a and b by G, L, I, and A respectively,

$G \leq L \leq I \leq A$

Sierpiński’s inequality

Posted on 5 January 2024 by John

Let A_n, G_n and H_n be the arithmetic mean, geometric mean, and harmonic mean of a set of n numbers.

When n = 2, the arithmetic mean times the harmonic mean is the geometric mean squared. The proof is simple:

$A_2(x, y) H_2(x, y) = \left(\frac{x + y}{2}\right)\left(\frac{2}{\frac{1}{x} + \frac{1}{y}} \right ) = xy = G_2(x,y)^2$

When n > 2 we no longer have equality. However, W. Sierpiński, perhaps best known for the Sierpiński’s triangle, proved that an inequality holds for all n. Given

$x = (x_1, x_2, \ldots, x_n)$

we have the inequality

$H_n(x)^{n-1}\, A_n(x) \leq G_n(x)^n \leq A_n(x)^{n-1}\, H_n(x)$

[1] W. Sierpinski. Sur une inégalité pour la moyenne alrithmétique, géometrique, et harmonique. Warsch. Sitzunsuber, 2 (1909), pp. 354–357.

Math

Bessel zero spacing

Related posts

Coloring the queen’s graph

Related posts

When is a function of two variables separable?

Related posts

Applications of Bernoulli differential equations

Related posts

The IQ Test That AI Can’t Pass

Means of means bounding the logarithmic mean

Related posts

When zeros at natural numbers implies zero everywhere

Related posts

Ky Fan’s inequality

Integral representations of means

Logarithmic mean

Geometric mean

Identric mean

Order of means

Related posts

Sierpiński’s inequality

Related posts