Orbital mechanics

The view from a Galilean moon

Posted on by John

The Galilean moons are the four largest moons of Jupiter, first observed by Galileo, contra Stigler’s law of eponymy.

This post shows what the Jovian system look like from the perspective of each of these moons, a sort of pre-Copernican perspective in a Jovian context.

The view from Io

Here’s what Europa would look like from Io. The orbital period for Europa is very nearly twice the orbital period of Io.

Here’s what Ganymede would look like from Io. The orbital period of Ganymede is very nearly 4 times that of Io.

Here’s what Callisto would look like from Io.

Here’s a combined view of the whole system, what Europa, Ganymede, Callisto, and Jupiter would look like from Io.

The view from Europa

The orbit of Io as seen from Europa is the same as the orbit of Europa as seen from Io.

Here’s what the orbit of Ganymede would look like from Europa. It’s similar to the view of Europa from Io because it is also a 2 : 1 resonance, i.e. the orbital period of Ganymede is approximately twice that of Europa.

Here’s what the orbit of Callisto would look like from Europa.

Here’s a combined view of the whole system, what Io, Ganymede, Callisto, and Jupiter would look like from Io.

The view from Ganymede

The view of Io from Ganymede is the same as the view of Ganymede from Io above. Similarly for Europa and Ganymede.

Here’s what the orbit of Callisto would look like from Ganymede. The two moons are in a 7 : 3 resonance.

Here’s a combined view of the whole system from Ganymede.

View of Callisto

The views of each of the moons from Callisto are presented above by symmetry. Here’s what the whole Jovian system would look like from Callisto.

View from Jupiter

Finally, here’s what the orbits of each of the moons looks like from Jupiter.

Related posts

What if Copernicus had been a Martian?

Posted on by John

The genius of Copernicus was to realize that this plot

view of Mars, Jupiter, and Saturn from Earth

becomes this plot

View of Earth, Mars, Jupiter, and Saturn from the sun

under a clever change of coordinates.

The first plot is the apparent motion of Mars, Jupiter, and Saturn as viewed from Earth over the course of 30 years. Of course Copernicus knew of Mercury and Venus as well, but I’ve omitted them to make the plot simpler. The second plot is the view of Earth, Mars, Jupiter, and Saturn from the sun.

If Copernicus had lived on Mars, what view of the solar system would he have started with? Here’s what 30 (Earth) years of the apparent motion of Earth, Jupiter, and Saturn would look like from Mars.

View of Earth, Jupiter, and Saturn from Mars

These plots were produced by modifying the Python script given in the previous post.

How the orbit of one planet appears from another

Posted on by John

This post shows how the orbits some planets appear from other planets. I’ve give a few of my favorite examples and include a Python program you could use to create your own plots.

We will assume the planets move in circles around the sun. They don’t exactly—they don’t exactly move in ellipses either—but their orbits are much closer to circles than most people realize. More on that here.

Venus / Earth

The ratio of Earth’s orbital period to that of Venus is almost exactly 13 to 8, so the view of Venus from Earth is nearly periodic with period 8 (Earth) years.

Venus from Earth

This is also the view of Earth from Venus. As the code below shows, the view of X from Y is the same as the view of Y from X.

Jupiter / Saturn

The ratio of Saturn’s orbital period to that of Jupiter is nearly 5 to 2. If this ratio were exactly, the figure below would repeat itself every two Saturnine years. But the following plot is over 4 Saturnine years, showing that years 3 and 4 don’t exactly retrace the path of years 1 and 2.

Jupiter from Saturn

Uranus / Earth

Here’s what the orbit of Uranus looks like from Earth.

Uranus from Earth

We see a big circle of tight little circles because the ratio of the distances from the sun is large.

Mercury / Venus

Here’s what Mercury looks like from Venus.

Mercury from Venus

Jovian moons

The same math that describes planets around the sun describes moons orbiting a planet. Here is what the orbit of Ganymede looks like from Callisto, and vice versa, as they orbit Jupiter. Ganymede completes 7 orbits in the time it takes Callisto to complete 3 orbits.

Ganymede and Callisto

Python code

Here’s the code that produced the plots.

    import matplotlib.pyplot as plt
    from numpy import linspace, sin, cos, pi
    
    period = {
        'mercury' : 87.96926,
        'venus'   : 224.7008,
        'earth'   : 365.25636,
        'mars'    : 686.97959,
        'ceres'   : 1680.22107,
        'jupiter' : 4332.8201,
        'saturn'  : 10755.699,
        'uranus'  : 20687.153,
        'neptune' : 60190.03
    }
    
    dist = lambda T : T**(2/3) # Kepler
    
    def plot_orbit(planet1, planet2, periods=10):
        T1 = period[planet1]
        T2 = period[planet2]
        d1 = dist(T1)
        d2 = dist(T2)

        theta = linspace(0, 2*pi*periods, 1000)
        x = d1*cos(T2*theta/T1) - d2*cos(theta)
        y = d1*sin(T2*theta/T1) - d2*sin(theta)

        plt.gca().set_aspect("equal")
        plt.axis('off')
        plt.plot(x, y)
        plt.show()
    
    plot_orbit("venus", "earth", 8)
    plot_orbit("jupiter", "saturn", 4)
    plot_orbit("uranus", "earth", 57)
    plot_orbit("mercury", "venus", 9)

Eccentricity, Flattening, and Aspect Ratio

Posted on by John

There are at least three common ways to describe the shape of an ellipse: eccentricity e, flattening f, and aspect ratio r. Each is a number between 0 and 1. (Flattening is also called ellipticity, which is a descriptive name, but unfortunately it sounds a lot like eccentricity.)

Although converting between these three descriptions is simple, it’s also a little counterintuitive. In particular, moderately large values of eccentricity correspond to small values of flattening. The previous post looked at how similar the orbits of all the planets are when you plot them all on the same scale. This is true even though the eccentricity of Venus is essentially 0 and the eccentricity of Pluto is 0.25.

Let a be the semi-major axis of the ellipse, the distance from the center to the furthest point of the ellipse.

Let b be the semi-minor axis of the ellipse, the distance from the center to the closest point on the ellipse.

Then the aspect ratio, flattening, and eccentricity are defined as follows:

\begin{align*} r &= \frac{b}{a} \\ f &= \frac{a-b}{a} \\ e &= \sqrt{1 - \frac{b^2}{a^2}} \\ \end{align*}

If we plot the orbits of all the planets, scaled so that b = 1 for all planets, then the distance to the furthest point in the orbit is 1/r. Here’s a graph of how 1/r varies as a function of e.

Notice that 1/r hardly changes as e varies between, say, 0 and 0.4. So saying that Pluto has a “highly elliptical” orbit with e = 0.25 does not mean that the shape of its orbit is far from a circle. Here’s a plot of all the planet orbits in our solar system, or all the planet orbits plus the orbit of Pluto if you’d like to be pedantic.

Converting between eccentricity, flattening, and aspect ratio

I made the comment on Twitter that the orbit of the earth around the sun is closer to being an exact circle than the lines of constant longitude are. This means that the fact that the earth’s equatorial bulge is more geometrically significant than the elliptical nature of our orbit.

If you want to confirm this statement, you’ll need to know the shape of earth’s orbit and the shape of a meridian. But you’re most likely to find the former described in terms of eccentricity and the latter in terms of flattening. This is an example of why you might want to convert between different ways of describing the shape of an ellipse. Here are the conversion formulas.

\begin{align*} e &= \sqrt{2f - f^2} \\ e &= \sqrt{1-r^2} \\ f &= 1-\sqrt{1-e^2} \\ f &= 1-r \\ r &= \sqrt{1-e^2} \\ r &= 1-f \\ \end{align*}

According to Wikipedia, the eccentricity of earth’s orbit is 0.01671 and the flattening is 1/298.3. To put these on a common scale, meridians have eccentricity: 0.08181, about five times the eccentricity of earth’s orbit.

Similarly, the earth’s orbit has flattening 0.00013962 or about 24 times the flattening of the meridians.

So you could say earth’s orbit is 4 times or 24 times closer to being a circle than earth’s meridians are. The two ratios are very different because the conversion between eccentricity and flattening is highly nonlinear.

Related posts

Planetary orbits are very nearly circular

Posted on by John

If a science book shows you obviously elliptical orbits of planets, it is literally stretching the truth.

I was taught that our benighted ancestors insisted that planetary orbits are circles for philosophical reasons. In fact, they insisted planetary orbits are circular because they very nearly are.

Here’s a plot of the orbits of all nine planets in our solar system, or all eight planets and the dwarf planet Pluto if you prefer, scaled so that they all have the same semi-minor axis.

See how far the “highly elliptical” orbit of Pluto extends past the perfect circle in the inside? Me neither.

Here is how Kepler discovered that planets have elliptical orbits [1].

From 1601 to 1608, he [Kepler] tried fitting various geometrical curves to Tycho’s data on the positions of Mars. Finally, after struggling for almost a year to remove a discrepancy of of 8 minutes of arc (which a less honest man might have chosen to ignore!) Kepler hit upon the ellipse as a possible solution.

It was only by obsessing over a discrepancy of 0.037% of a circle that Kepler was able to discover that Mars has an elliptical orbit.

The next post explains why eccentricity numbers are misleading. The orbit of Pluto, for example, is “highly eccentric” with eccentricity 0.25, but this does not result in an orbit far from circular.

[1] Roger Bate et al. Fundamentals of Astrodynamics. Dover. 1971

The Pluto-Charon orbit

Posted on by John

The Moon doesn’t orbit the center of the Earth; it orbits the center of mass of the Earth-Moon system, which is inside the Earth. The distinction matters for designing satellite orbits, but it cannot be seen on a plot to scale. We’ll quantify this below.

Pluto’s moon Charon, however, is so large relative to Pluto and so close, that the center of mass of the Pluto-Charon system is outside of Pluto, and you can easily see this in a plot.

Plot of Pluto and Charon orbiting their barycenter

Imagine Pluto and Charon sitting on each end of a balanced seesaw. Pluto is a distance x1 to the left of the fulcrum, and Charon is a distance x2 to the right of the fulcrum. Let m1 be the mass of Pluto and m2 be the mass of Charon. Then

m1 x1 = m2 x2

and

x1 = m2 (x1 + x2) / (m1 + m2).

Now let’s put in some numbers.

m1 = 1.309 × 1022 kg
m2 = 1.62 × 1021 kg
x1 + x2 = 19,640 km

From this we find

x1 = (1.62 × 19640 / 14.71) km = 2163 km

and so the distance from the center of Pluto to the center of mass of the Pluto-Charon system is 2163 km. But the radius of Pluto is only 1190 km. So the center of mass of the Pluto-Charon system is about as far above the surface of Pluto as the center of Pluto is below the surface.

Comparison with the Earth-Moon system

It matters that the moon doesn’t exactly orbit the center of the Earth, but the difference between the center of the Earth and the center of mass of the Earth-Moon system is less dramatic. Let’s put in the numbers for the Earth and Moon.

m1 = 5.97 × 1024 kg
m2 = 7.346 × 1022 kg
x1 + x2 = 392,600 km

From this we find

x1 = (7.346 × 392,600 / 604) km = 4,775 km

The radius of Earth is 6,371 km, and so the center of mass of the Earth-Moon system is inside the Earth.

I made a plot analogous to the one above but for the Earth-Moon system. You could barely see the moon because it is so small relative to the size of its orbit. And you cannot see the difference between the center of the Earth and the barycenter of the Earth and Moon.

Tidal locking

Not only is Charon tidally locked with Pluto, as our moon is with Earth, but Pluto is tidally locked with Charon as well.

On Earth we only ever see one side of the moon. We never see the “dark side,” which is more accurately the “far side.” But someone standing on the moon would see Earth rotate.

Someone standing on Pluto would only ever see one side of Charon, and someone standing on Charon would only ever see one side of Pluto. Sputnik Planitia, the big heart-shaped feature on Pluto, is on the opposite side of Charon, so you could say Pluto is hiding its heart from its companion.

Image of Pluto featuring heart-shaped region

More orbital mechanics posts

Shape of moon orbit around sun

Posted on by John

The earth’s orbit around the sun is nearly a circle, and the moon’s orbit around the earth is nearly a circle, but what is the shape of the moon’s orbit around the sun?

You might expect it to be bumpy, bending inward when the moon is between the earth and the sun and bending output when the moon is on the opposite side of the earth from the sun. But in fact the shape of the moon’s orbit around the sun is convex as proved in [1] and illustrated below.

If the moon orbited the earth much faster, say 10 times faster, at the same altitude, then we see that the orbit is indeed bumpy.

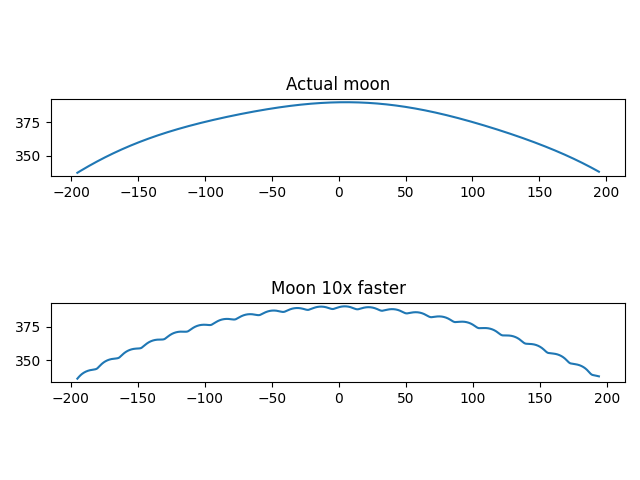
However, the nothing could orbit the earth 10x faster than the moon at the same distance as the moon. Orbital period determines altitude and vice versa.

A more realistic example would be a satellite in MEO (Medium Earth Orbit) like a GPS satellite. Such a satellite orbits the earth roughly twice a day. The path of a MEO satellite around the sun is not convex.

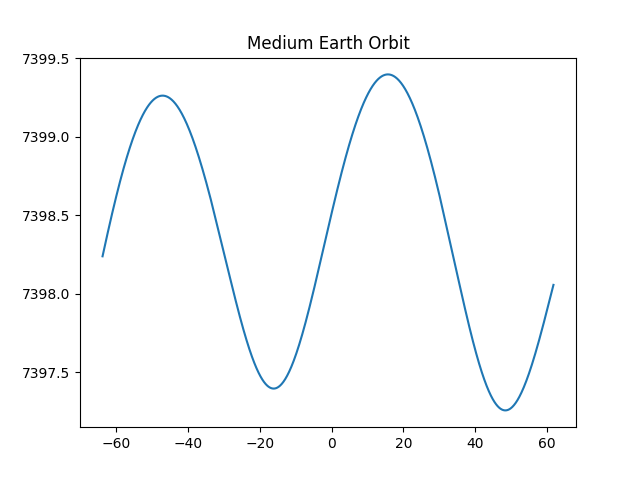
The plot above shows about one day of an MEO satellite’s orbit around the sun. Note that the vertical and horizontal scales are not the same; it would be hard to see anything but a flat line if the scales were the same because the satellite is far closer to the earth than the sun.

Here are the equations from [1]. Choose units so that the distance to the moon or satellite is 1 and let d be the distance from the planet to the sun. Let p be the number of times the moon or satellite orbits the planet as the planet orbits the sun (the number of sidereal periods).

x(θ) = d cos(θ) + cos(pθ)
y(θ) = d sin(θ) + sin(pθ)

This assumes both the planet’s orbit around the sun and the satellite’s orbit around the planet are circular, which is a good approximation in our examples.

[1] Noah Samuel Brannen. The Sun, the Moon, and Convexity. The College Mathematics Journal, Vol. 32, No. 4 (Sep., 2001), pp. 268-272

Solar declination

Posted on by John

This post expands on a small part of the post Demystifying the Analemma by M. Tirado.

Apparent solar declination given δ by

δ = sin−1( sin(ε) sin(θ) )

where ε is axial tilt and θ is the angular position of a planet. See Tirado’s post for details. Here I want to unpack a couple things from the post. One is that that declination is approximately

δ = ε sin(θ),

the approximation being particular good for small ε. The other is that the more precise equation approaches a triangular wave as ε approaches a right angle.

Let’s start out with ε = 23.4° because that is the axial tilt of the Earth. The approximation above is a variation on the approximation

sin φ ≈ φ

for small φ when φ is measured in radians. More on that here.

An angle of 23.4° is 0.4084 radians. This is not particularly small, and yet the approximation above works well. The approximation above amounts to approximating sin−1(x) with x, and Taylor’s theorem tells the error is about x³/6, which for x = sin(ε) is about 0.01. You can’t see the difference between the exact and approximate equations from looking at their graphs; the plot lines lie on top of each other.

Even for a much larger declination of 60° = 1.047 radians, the two curves are fairly close together. The approximation, in blue, slightly overestimates the exact value, in gold.

This plot was produced in Mathematica with

    ε = 60 Degree
    Plot[{ε Sin[θ] ], ArcSin[Sin[ε] Sin[θ]]}, {θ, 0, 2π}]

As ε gets larger, the curves start to separate. When ε = 90° the gold curve becomes exactly a triangular wave.

Update: Here’s a plot of the maximum approximation error as a function of ε.

Related posts

When do two-body systems have stable Lagrange points?

Posted on by John

The previous post looked at two of the five Lagrange points of the Sun-Earth system. These points, L1 and L2, are located on either side of Earth along a line between the Earth and the Sun. The third Lagrange point, L3, is located along that same line, but on the opposite side of the Sun.

L1, L2, and L3 are unstable, but stable enough on a short time scale to be useful places to position probes. Lagrange points are in the news this week because the James Webb Space Telescope (JWST), launched on Christmas Day, is headed toward L2 at the moment.

The remaining Lagrange points, L4 and L5, are stable. These points are essentially in Earth’s orbit around the Sun, 60° ahead and 60° behind Earth. To put it another way, they’re located where Earth will be in two months and where Earth was two months ago. The points L3, L4, and L5 form an equilateral triangle centered at the Sun.

Lagrange points more generally

Lagrange points are not unique to the Sun and Earth, but also holds for other systems as well. You have two bodies m1 and m2 , such as a star and a planet or a planet and a moon, and a third body, such as the JWST, with mass so much less than the other two that its mass is negligible compared to the other two bodies.

The L1, L2, and L3 points are always unstable, meaning that an object placed there will eventually leave, but the L4 and L5 points are stable, provided one of the bodies is sufficiently less massive than the other. This post will explore just how much less massive.

Mass ratio requirement

Michael Spivak [1] devotes a section of his physics book to the Trojan asteroids, asteroids that orbit the Sun at the L4 and L5 Lagrange points of a Sun-planet system. Most Trojan asteroids are part of the Sun-Jupiter system, but other planets have Trojan asteroids as well. The Earth has a couple Trojan asteroids of its own.

Spivak shows that in order for L4 and L5 to be stable, the masses of the two objects must satisfy

(m1 – m2) / (m1 + m2) > k

where m1 is the mass of the more massive body, m2 is the mass of the less massive body, and

k = √(23/27).

If we define r to be the ratio of the smaller mass to the larger mass,

r = m2 / m1,

then by dividing by m1 we see that equivalently we must have

(1 − r) / (1 + r) > k.

We run into the function (1 − z)/(1 + z) yet again. As we’ve pointed out before, this function is its own inverse, and so the solution for r is that

r < (1 − k) / (1 + k) = 0.04006…

In other words, the more massive body must be at least 25 times more massive than the smaller body.

The Sun is over 1000 times more massive than Jupiter, so Jupiter’s L4 and L5 Lagrange points with respect to the Sun are stable. The Earth is over 80 times more massive than the Moon, so the L4 and L5 points of the Earth-Moon system are stable as well.

Pluto has only 8 times the mass of its moon Charon, so the L4 and L5 points of the Pluto-Charon system would not be stable.

Related posts

[1] Michael Spivak: Physics for Mathematicians: Mechanics I. Addendum 10A.

Finding Lagrange points L1 and L2

Posted on by John

The James Webb Space Telescope (JWST) is on its way to the Lagrange point L2 of the Sun-Earth system. Objects in this location will orbit the Sun at a fixed distance from Earth.

There are five Lagrange points, L1 through L5. The points L1, L2, and L3 are unstable, and points L4 and L5 are stable. Since L2 is unstable, it will have to adjust its orbit occasionally to stay at L2.

The Lagrange points L1 and L2 are nearly equally distant from Earth, with L1 between the Earth and Sun, and L2 on the opposite side of Earth from the Sun.

The equations for the distance r from L1 and L2 to Earth are very similar and can be combined into one equation:

\frac{M_1}{(R\pm r)^2} \pm \frac{M_2}{r^2}=\left(\frac{M_1}{M_1+M_2}R \pm r\right)\frac{M_1+M_2}{R^3}

The equation for L1 corresponds to taking ± as – and the equation for L2 corresponds to taking ± as +.

In the equation above, R is the distance between the Sun and Earth, and M1 and M2 are the mass of the Sun and Earth respectively. (This is not going to be too precise since the distance between the Sun and Earth is not constant. We’ll use the mean distance for R.)

For both L1 and L2 we have

r \approx R \sqrt[3]{\frac{M_2}{3M_1}}

Let’s use Newton’s method to solve for the distances to L1 and L2, and see how they compare to the approximation above.

    from scipy.optimize import newton
    
    M1 = 1.988e30 # kg
    M2 = 5.972e24 # kg
    R  = 1.471e8  # km

    approx = R*(M2/(3*M1))**(1/3)
    
    def f(r, sign):
        M = M1 + M2
        ret = M1/(R + sign*r)**2 + sign*M2/r**2
        ret -= (R*M1/M + sign*r)*M/R**3
        return ret
    
    L1 = newton(lambda r: f(r, -1), approx)
    L2 = newton(lambda r: f(r,  1), approx)
    
    print("L1       = ", L1)
    print("approx   = ", approx)
    print("L2       = ", L2)
    print("L1 error = ", (approx - L1)/L1)
    print("L2 error = ", (L2 - approx)/L2)

This prints the following.

    
    L1       = 1467000
    approx   = 1472000
    L2       = 1477000
    L1 error = 0.3357%
    L2 error = 0.3312%

So L2 is slightly further away than L1. The approximate distance under-estimates L2 and over-estimates L1 both by about 0.33% [1].

L1 and L2 are about 4 times further away than the moon.

Related posts

[1] The approximation for r makes an excellent starting point. When I set the relative error target to 1e−5, Newton’s method converged in four iterations.

    full = newton(lambda r: f(r, 1), approx, tol=1e-5, full_output=True)
    print(full)