Interpreting statistics

Posted on 13 January 2012 by John

I challenge you to find me in any published statistical analysis, outside of an introductory textbook, a confidence interval given the correct interpretation. If you can find even one instance where the [frequentist] confidence interval is not interpreted as a [Bayesian] credible interval, then I will eat your hat.

Most statistical analysis is carried out by people who do not interpret their results correctly. They carry out frequentist procedures and then give the results a Bayesian interpretation. This is not simply a violation of an academic taboo. It means that people generally underestimate the uncertainty in their conclusions.

Bad logic, but good statistics

Posted on 28 November 2011 by John

Ad hominem arguments are bad logic, but good (Bayesian) statistics. A statement isn’t necessarily false because it comes from an unreliable source, though it is more likely to be false.

Some people are much more likely to know what they’re talking about than others, depending on context. You’re more likely to get good medical advice from a doctor than from an accountant, though the former may be wrong and the latter may be right. (Actors are not likely to know what they’re talking about when giving advice regarding anything but acting, though that doesn’t stop them.)

Ad hominem guesses are a reasonable way to construct a prior, but the prior needs to be updated with data. Given no other data, the doctor is more likely to know medicine than the accountant is. Assuming a priori that both are equally likely to be correct may be “fair,” but it’s not reasonable. However, as you gather data on the accuracy of each, you could change your mind. The posterior distribution could persuade you that you’ve been talking to a quack doctor or an accountant who is unusually knowledgeable of medicine.

Related post: Musicians, drunks, and Oliver Cromwell

Leading digits of factorials

Posted on 19 October 2011 by John

Suppose you take factorials of a lot of numbers and look at the leading digit of each result. You could argue that there’s no apparent reason that any digit would be more common than any other, so you’d expect each of the digits 1 through 9 would come up 1/9 of the time. Sounds plausible, but it’s wrong.

The leading digits of factorials follow Benford’s law as described in the previous post. In fact, factorials follow Benford’s law even better than physical constants do. Here’s a graph of the leading digits of the factorials of 1 through 500.

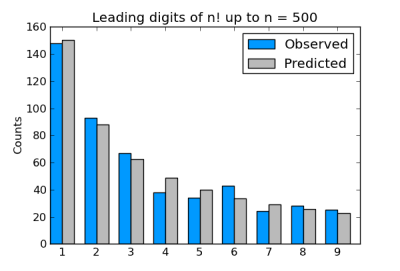
In the remainder of this post, I’ll explain why Benford’s law should apply to factorials, make an aside on statistics, and point out an interesting feature of the Python code used to generate the chart above.

Why Benford’s law applies

Here’s a hand-waving explanation. One way to justify Benford’s law is to say that physical constants are uniformly distributed, but on a logarithmic scale. The same is true for factorials, and it’s easier to see why.

The leading digits of the logarithms depend on their logarithms in base 10. The gamma function extends the factorial function and it is log-convex. The logarithm of the gamma function is fairly flat (see plot here), and so the leading digits of the log-gamma function applied to integers are uniformly distributed on a logarithmic scale. (I’ve mixed logs base 10 and natural logs here, but that doesn’t matter. All logarithms are the same up to a multiplicative constant. So if a plot is nearly linear on a log10 scale, it’s nearly linear on a natural log scale.)

Update: Graham gives a link in the comments below to a paper proving that factorials satisfy Benford’s law exactly in the limit.

Uniform on what scale?

This example brings up an important principle in statistics. Some say that if you don’t have a reason to assume anything else, use a uniform distribution. For example, some say that a uniform prior is the ideal uninformative prior for Bayesian statistics. But you have to ask “Uniform on what scale?” It turns out that the leading digits of physical constants and factorials are indeed uniformly distributed, but on a logarithmic scale.

Python integers and floating point

I used nearly the same code to produce the chart above as I used in its counterpart in the previous post. However, one thing had to change: I couldn’t compute the leading digits of the factorials the same way. Python has extended precision integers, so I can compute 500! factorial without overflowing. Using floating point numbers, I could only go up to 170!. But when I used my previous code to find the leading digit, it first tried to apply log10 to an integer larger than the largest representable floating point number and failed. Converting numbers such as 500! to floating point numbers will overflow. (See Floating point numbers are a leaky abstraction.)

The solution was to find the leading digit using only integer operations.

    def leading_digit_int(n):
        while n > 9:
            n = n/10
        return n

This code works fine for numbers like 500! or even larger.

A Bayesian view of Amazon Resellers

Posted on 27 September 2011 by John

I was buying a used book through Amazon this evening. Three resellers offered the book at essentially the same price. Here were their ratings:

94% positive out of 85,193 reviews
98% positive out of 20,785 reviews
99% positive out of 840 reviews

Which reseller is likely to give the best service? Before you assume it’s the seller with the highest percentage of positive reviews, consider the following simpler scenario.

Suppose one reseller has 90 positive reviews out of 100. The other reseller has two reviews, both positive. You could say one has 90% approval and the other has 100% approval, so the one with 100% approval is better. But this doesn’t take into consideration that there’s much more data on one than the other. You can have some confidence that 90% of the first reseller’s customers are satisfied. You don’t really know about the other because you have only two data points.

A Bayesian view of the problem naturally incorporates the amount of data as well as its average. Let θ_A be the probability of a customer being satisfied with company A‘s service. Let θ_B be the corresponding probability for company B. Suppose before we see any reviews we think all ratings are equally likely. That is, we start with a uniform prior distribution θ_A and θ_B. A uniform distribution is the same as a beta(1, 1) distribution.

After observing 90 positive reviews and 10 negative reviews, our posterior estimate on θ_A has a beta(91, 11) distribution. After observing 2 positive reviews, our posterior estimate on θ_B has a beta(3, 1) distribution. The probability that a sample from θ_A is bigger than a sample from θ_B is 0.713. That is, there’s a good chance you’d get better service from the reseller with the lower average approval rating.

beta(91,11) versus beta(3,1)

Now back to our original question. Which of the three resellers is most likely to satisfy a customer?

Assume a uniform prior on θ_X, θ_Y, and θ_Z, the probabilities of good service for each reseller. The posterior distributions on these variables have distributions beta(80082, 5113), beta(20370, 417), and beta(833, 9).

These beta distributions have such large parameters that we can approximate them by normal distributions with the same mean and variance. (A beta(a, b) random variable has mean a/(a+b) and variance ab/((a+b)²(a+b+1)).) The variable with the most variance, θ_Z, has standard deviation 0.003. The other variables have even smaller standard deviation. So the three distributions are highly concentrated at their mean values with practically non-overlapping support. And so a sample from θ_X or θ_Y is unlikely to be higher than a sample from θ_Z.

In general, going by averages alone works when you have a lot of customer reviews. But when you have a small number of reviews, going by averages alone could be misleading.

Thanks to Charles McCreary for suggesting the xkcd comic.

Big data and humility

Posted on 22 September 2011 by John

One of the challenges with big data is to properly estimate your uncertainty. Often “big data” means a huge amount of data that isn’t exactly what you want.

As an example, suppose you have data on how a drug acts in monkeys and you want to infer how the drug acts in humans. There are two sources of uncertainty:

How well do we really know the effects in monkeys?
How well do these results translate to humans?

The former can be quantified, and so we focus on that, but the latter may be more important. There’s a strong temptation to believe that big data regarding one situation tells us more than it does about an analogous situation.

I’ve seen people reason as follows. We don’t really know how results translate from monkeys to humans (or from one chemical to a related chemical, from one market to an analogous market, etc.). We have a moderate amount of data on monkeys and we’ll decimate it and use that as if it were human data, say in order to come up with a prior distribution.

Down-weighting by a fixed ratio, such as 10 to 1, is misleading. If you had 10x as much data on monkeys, would you as much about effects in humans as if the original smaller data set were collected on people? What if you suddenly had “big data” involving every monkey on the planet. More data on monkeys drives down your uncertainty about monkeys, but does nothing to lower your uncertainty regarding how monkey results translate to humans.

At some point, more data about analogous cases reaches diminishing return and you can’t go further without data about what you really want to know. Collecting more and more data about how a drug works in adults won’t help you learn how it works in children. At some point, you need to treat children. Terabytes of analogous data may not be as valuable as kilobytes of highly relevant data.

Bayes isn’t magic

Posted on 6 September 2011 by John

If a study is completely infeasible using traditional statistical methods, Bayesian methods are probably not going to rescue it. Bayesian methods can’t squeeze blood out of a turnip.

The Bayesian approach to statistics has real advantages, but sometimes these advantages are oversold. Bayesian statistics is still statistics, not magic.

Markov chains don’t converge

Posted on 10 August 2011 by John

I often hear people often say they’re using a burn-in period in MCMC to run a Markov chain until it converges. But Markov chains don’t converge, at least not the Markov chains that are useful in MCMC. These Markov chains wander around forever exploring the domain they’re sampling from. Any point that makes a “bad” starting point for MCMC is a point you might reach by burn-in.

Not only that, Markov chains can’t remember how they got where they are. That’s their defining property. So if your burn-in period ends at a point x, the chain will perform exactly as if you had simply started at x.

When someone says a Markov chain has converged, they may mean that the chain has entered a high-probability region. I’ll explain in a moment why that’s desirable. But the belief/hope is that a burn-in period will put a Markov chain in a high-probability region. And it probably will, but there are a couple reasons why this isn’t necessarily the best thing to do.

Burn-in may be ineffective. You could use optimization to be certain that you’re starting in such a region. Burn-in offers no such assurance. See Burn-in and other MCMC folklore.
Burn-in may be inefficient. Casting aside worries that burn-in may not do what you want, it can be an inefficient way to find a high-probability region. MCMC isn’t designed to optimize a density function but rather to sample from it.

Why use burn-in? MCMC practitioners often don’t know how to do optimization, and in any case the corresponding optimization problem may be difficult. Also, if you’ve got the MCMC code in hand, it’s convenient to use it to find a starting point as well as for sampling.

So why does it matter whether you start your Markov chain in a high-probability region? In the limit, it doesn’t matter. But since you’re averaging some function of some finite number of samples, your average will be a better approximation if you start at a typical point in the density you’re sampling. If you start at a low probability location, your average may be more biased.

Samples from Markov chains don’t converge, but averages of functions applied to these samples may converge. When someone says a Markov chain has converged, they may mean they’re at a point where the average of a finite number of function applications will be a better approximation of the thing they want to compute than if they’d started at a low probability point.

It’s not just a matter of imprecise language when people say a Markov chain has converged. It sometimes betrays a misunderstanding of how Markov chains work.

Teaching Bayesian stats backward

Posted on 20 April 2011 by John

Most presentations of Bayesian statistics I’ve seen start with elementary examples of Bayes’ Theorem. And most of these use the canonical example of testing for rare diseases. But the connection between these examples and Bayesian statistics is not obvious at first. Maybe this isn’t the best approach.

What if we begin with the end in mind? Bayesian calculations produce posterior probability distributions on parameters. An effective way to teach Bayesian statistics might be to start there. Suppose we had probability distributions on our parameters. Never mind where they came from. Never mind classical objections that say you can’t do this. What if you could? If you had such distributions, what could you do with them?

For starters, point estimation and interval estimation become trivial. You could, for example, use the distribution mean as a point estimate and the area between two quantiles as an interval estimate. The distributions tell you far more than point estimates or interval estimates could; these estimates are simply summaries of the information contained in the distributions.

It makes logical sense to start with Bayes’ Theorem since that’s the tool used to construct posterior distributions. But I think it makes pedagogical sense to start with the posterior distribution and work backward to how one would come up with such a thing.

Bayesian statistics is so named because Bayes’ Theorem is essential to its calculations. But that’s a little like classical statistics Central Limitist statistics because it relies heavily on the Central Limit Theorem.

The key idea of Bayesian statistics is to represent all uncertainty by probability distributions. That idea can be obscured by an early emphasis on calculations.

Significance testing and Congress

Posted on 14 April 2011 by John

The US Supreme Court’s criticism of significance testing has been in the news lately. Here’s a criticism of significance testing involving the US Congress. Consider the following syllogism.

If a person is an American, he is not a member of Congress.
This person is a member of Congress.
Therefore he is not American.

The initial premise is false, but the reasoning is correct if we assume the initial premise is true.

The premise that Americans are never members of Congress is clearly false. But it’s almost true! The probability of an American being a member of Congress is quite small, about 535/309,000,000. So what happens if we try to salvage the syllogism above by inserting “probably” in the initial premise and conclusion?

If a person is an American, he is probably not a member of Congress.
This person is a member of Congress.
Therefore he is probably not American.

What went wrong? The probability is backward. We want to know the probability that someone is American given he is a member of Congress, not the probability he is a member of Congress given he is American.

Science continually uses flawed reasoning analogous to the example above. We start with a “null hypothesis,” a hypothesis we seek to disprove. If our data are highly unlikely assuming this hypothesis, we reject that hypothesis.

If the null hypothesis is correct, then these data are highly unlikely.
These data have occurred.
Therefore, the null hypothesis is highly unlikely.

Again the probability is backward. We want to know the probability of the hypothesis given the data, not the probability of the data given the hypothesis.

We can’t reject a null hypothesis just because we’ve seen data that are rare under this hypothesis. Maybe our data are even more rare under the alternative. It is rare for an American to be in Congress, but it is even more rare for someone who is not American to be in the US Congress!

I found this illustration in The Earth is Round (p < 0.05) by Jacob Cohen (1994). Cohen in turn credits Pollard and Richardson (1987) in his references.

Like Laplace, only more so

Posted on 17 February 2011 by John

The Laplace distribution is pointy in the middle and fat in the tails relative to the normal distribution.This post is about a probability distribution that is more pointy in the middle and fatter in the tails.

Here are pictures of the normal and Laplace (a.k.a. double exponential) distributions.

Normal:

Laplace:

The normal density is proportional to exp(− x²/2) and the Laplace distribution is proportional to exp(-|x|). Near the origin, the normal density looks like 1 − x²/2 and the Laplace density looks like 1 − |x|. And as x gets large, the normal density goes to zero much faster than the Laplace.

Now let’s look at the distribution with density

f(x) = log(1 + 1/x²)

I don’t know a name for this. I asked on Cross Validated whether there was a name for this distribution and no knew of one. The density is related to the bounds on a density presented in this paper. Here’s a plot.

The density is unbounded near the origin, blowing up like −2 log( |x| ) as x approaches 0, and so is more pointed than the Laplace density. As x becomes large, log(1 + x⁻²) is asymptotically x⁻² so the distribution has the same tail behavior as a Cauchy distribution, much heavier tailed than the Laplace density.

Here’s a plot of this new density and the Laplace density together to make the contrast more clear.

As William Huber pointed out in his answer on Cross Validated, this density has a closed-form CDF:

F(x) = 1/2 + (arctan(x) − x log( sin( arctan(x) ) ))/π

The paper mentioned above used a similar density as a Bayesian prior distribution in situations where many observations were expected to be small, though large values were expected as well.

Bayesian

Interpreting statistics

More statistical posts