Python

Calculating the period of Van der Pol oscillators

Posted on by John

A few days ago I wrote about how to solve differential equations with SciPy’s ivp_solve function using Van der Pol’s equation as the example. Van der Pol’s equation is

{d^2x \over dt^2}-\mu(1-x^2){dx \over dt}+x= 0

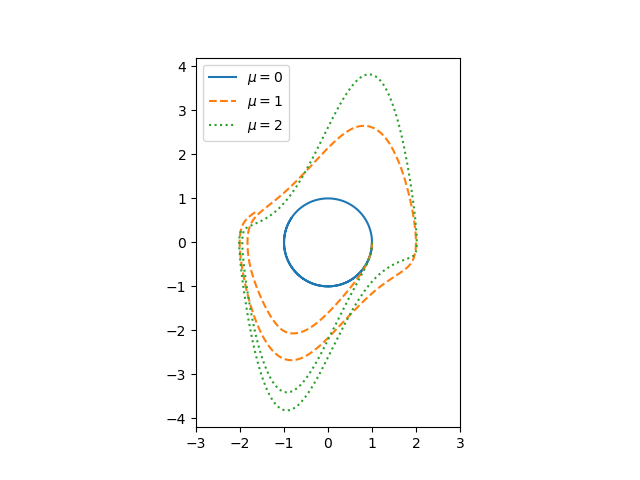
The parameter μ controls the amount of nonlinear damping. For any initial condition, the solution approach a periodic solution. The limiting periodic function does not depend on the initial condition [1] but does depend on μ. Here are the plots for μ  = 0, 1, and 2 from the previous post.

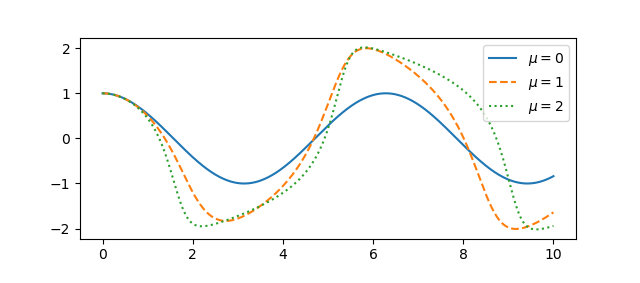
Van der Pol oscillator solutions as a function of time

A couple questions come to mind. First, how quickly do the solutions become periodic? Second, how does the period depend on μ? To address these questions, we’ll use an optional argument to ivp_solve we didn’t need in the earlier post.

Using events in ivp_solve

For ivp_solve an event is a function of the time t and the solution y whose roots the solver will report. To determine the period, we’ll look at where the solution is zero; our event function is trivial since we want to find the roots of the solution itself.

Recall from the earlier post that we cast our second order ODE as a pair of first order ODEs, and so our solution is a vector, the function x and its derivative. So to find roots of the solution, we look at what the solver sees as the first component of the solver. So here’s our event function:

    def root(t, y): return y[0]

Let’s set μ = 2 and find the zeros of the solution over the interval [0, 40], starting from the initial condition x(0) = 1, x‘(0) = 0.

    mu = 2
    sol = solve_ivp(vdp, [0, 40], [1, 0], events=root)
    zeros = sol.t_events[0]

Here we reuse the vdp function from the previous post about the Van der Pol oscillator.

To estimate the period of the limit cycle we look at the spacing between zeros, and how that spacing is changing.

    spacing = zeros[1:] - zeros[:-1]
    deltas = spacing[1:] - spacing[:-1]

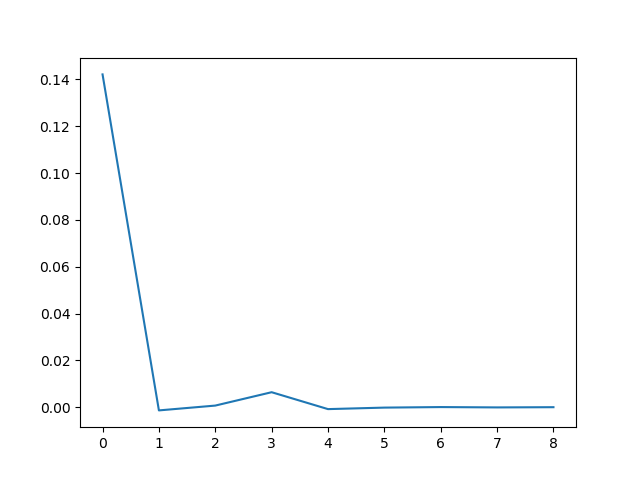
If we plot the deltas we see that the zero spacings quickly approach a constant value. Zero crossings are half periods, so the period of the limit cycle is twice the limiting spacing between zeros.

Van der pol period deltas

Theoretical results

If μ = 0 the Van der Pol oscillator reduces to a simple harmonic oscillator and the period is 2π. As μ increases, the period increases.

For relatively small μ we can calculate the period as above, but as μ increases this becomes more difficult numerically [2]. But one can easily show that the period is asymptotically

T ~ (3 – 2 log 2) μ

as μ goes to infinity. A more refined estimate due to Mary Cartwright is

T ~ (3 – 2 log 2) μ + 2π/μ1/3

for large μ.

More VdP posts

[1] There is a trivial solution, x = 0, corresponding to the initial conditions x(0) = x‘(0) = 0. Otherwise, every set of initial conditions leads to a solution that converges to the periodic attractor.

[2] To see why large values of μ are a problem numerically, here’s a plot of a solution for μ = 100.

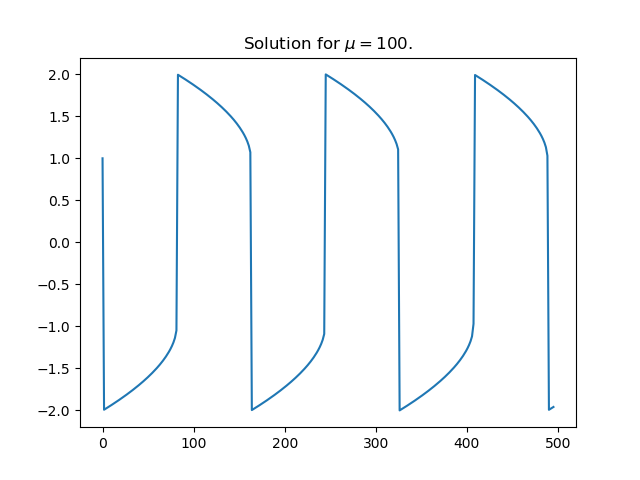
Solution to Van der Pol for large damping parameter mu

The solution is differentiable everywhere, but the derivative changes so abruptly at the maxima and minima that it is discontinuous for practical purposes.

Solving Van der Pol equation with ivp_solve

Posted on by John

Van der Pol’s differential equation is

{d^2x \over dt^2}-\mu(1-x^2){dx \over dt}+x= 0

The equation describes a system with nonlinear damping, the degree of nonlinearity given by μ. If μ = 0 the system is linear and undamped, but as μ increases the strength of the nonlinearity increases. We will plot the phase portrait for the solution to Van der Pol’s equation in Python using SciPy’s new ODE solver ivp_solve.

The function ivp_solve does not solve second-order systems of equations directly. It solves systems of first-order equations, but a second-order differential equation can be recast as a pair of first-order equations by introducing the first derivative as a new variable.

\begin{align*} {dx \over dt} &= y \\ {dy \over dt}&= \mu(1-x^2)y -x \\ \end{align*}

Since y is the derivative of x, the phase portrait is just the plot of (x, y).

Phase portait of Van der Pol oscillator

If μ = 0, we have a simple harmonic oscillator and the phase portrait is simply a circle. For larger values of μ the solutions enter limiting cycles, but the cycles are more complicated than just circles. These limiting cycles are periodic attractors: every non-trivial solution converges to the limit cycle.

Here’s the Python code that made the plot.

from scipy import linspace
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

def vdp(t, z):
    x, y = z
    return [y, mu*(1 - x**2)*y - x]

a, b = 0, 10

mus = [0, 1, 2]
styles = ["-", "--", ":"]
t = linspace(a, b, 500)

for mu, style in zip(mus, styles):
    sol = solve_ivp(vdp, [a, b], [1, 0], t_eval=t)
    plt.plot(sol.y[0], sol.y[1], style)
  
# make a little extra horizontal room for legend
plt.xlim([-3,3])    
plt.legend([f"$\mu={m}$" for m in mus])
plt.axes().set_aspect(1)

To plot the solutions as a function of time, rather than plotting phase portraits, change the line

    plt.plot(sol.y[0], sol.y[1], style)

to

    plt.plot(sol.t, sol.y[0], style)

and comment out the line setting xlim This gives the following plot.

Van der Pol oscillator solutions as a function of time

More dynamical system posts

Data Science and Star Science

Posted on by John

I recently got a review copy of Statistics, Data Mining, and Machine Learning in Astronomy. I’m sure the book is especially useful to astronomers, but those of us who are not astronomers could use it as a survey of data analysis techniques, especially using Python tools, where all the examples happen to come from astronomy. It covers a lot of ground and is pleasant to read.

Generating Python code from SymPy

Posted on by John

Yesterday I wrote about Householder’s higher-order generalizations of Newton’s root finding method. For n at least 2, define

H_n(x) = x + (n-1) \frac{\left( \frac{1}{f(x)}\right)^{(n-2)}}{\left( \frac{1}{f(x)}\right)^{(n-1)}}

and iterate Hn to find a root of f(x). When n = 2, this is Newton’s method. In yesterday’s post I used Mathematica to find expressions for H3 and H4, then used Mathematica’s FortranForm[] function to export Python code. (Mathematica doesn’t have a function to export Python code per se, but the Fortran syntax was identical in this case.)

Aaron Muerer pointed out that it would have been easier to generate the Python code in Python using SymPy to do the calculus and labdify() to generate the code. I hadn’t heard of lambdify before, so I tried out his suggestion. The resulting code is nice and compact.

    from sympy import diff, symbols, lambdify

    def f(x, a, b):
        return x**5 + a*x + b

    def H(x, a, b, n):
        x_, a_, b_ = x, a, b
        x, a, b = symbols('x a b')
        expr = diff(1/f(x,a,b), x, n-2) / \
               diff(1/f(x,a,b), x, n-1)
        g = lambdify([x,a,b], expr)
        return x_ + (n-1)*g(x_, a_, b_)

This implements all the Hn at once. The previous post implemented three of the Hn separately.

The first couple lines of H require a little explanation. I wanted to use the same names for the numbers that the function H takes and the symbols that SymPy operated on, so I saved the numbers to local variables.

This code is fine for a demo, but in production you’d want to generate the function g once (for each n) and save the result rather than generating it on every call to H.

Calling Python from Mathematica

Posted on by John

The Mathematica function ExternalEvalute lets you call Python from Mathematica. However, there are a few wrinkles.

I first pasted in an example from the Mathematica documentation and it failed.

    ExternalEvaluate[
        "Python", 
        {"def f(x): return x**2", "f(3)"}
    ]

It turns out you (may) have to tell Mathematica where to find Python. I ran the following, tried again, and the example worked.

    RegisterExternalEvaluator[
        "Python", 
        "C:\\bin\\Anaconda3\\python.EXE"
    ]

You can also run Python with NumPy loaded using

    ExternalEvaluate["Python-NumPy", … ]

except that didn’t work the first time either. You have to register a Python-NumPy evaluator separately. So I ran

    RegisterExternalEvaluator[
        "Python-NumPy", 
        "C:\\bin\\Anaconda3\\python.EXE"
    ]

and then tried again calling Python code using NumPy. But then there’s the question of how it imports NumPy. Does it simply run import numpy, or maybe from numpy import *, or maybe import numpy as np? It turns out the first possibility is what happens. So to print pi from NumPy, your code string needs to be numpy.pi.

You don’t need to use Python-NumPy if you just do your own importing. For example, this code returns π².

    ExternalEvaluate[
        "Python", 
        "import numpy; x = numpy.pi; x**2"
    ]

And you can import any library you’d like, not just NumPy.

    ExternalEvaluate[
        "Python", 
        "from sympy import isprime; isprime(7)"
    ]

Everything above applies to Mathematica 11.3 and Mathematica 12.

Squircle perimeter and the isoparametric problem

Posted on by John

If you have a fixed length of rope and you want to enclose the most area inside the rope, make it into a circle. This is the solution to the so-called isoparametric problem.

Dido’s problem is similar. If one side of your bounded area is given by a straight line, make your rope into a semi-circle.

This post looks at a similar problem for a squircle. Peter Panholzer mentioned the problem of finding the squircle exponent that led to the largest area in proportion to its arclength. This sounds like the isoparametric problem, but it’s not.

The isoparametric problem holds perimeter constant and lets the shape enclosed vary, maximizing the area. The question here is to hold the axes constant and maximize the ratio of the area to the perimeter. Panholzer reports the maximum occurs at p = 4.39365.

Computing the perimeter

The volume of a squircle can be found in closed form, and I’ve mentioned the equation a few times, for example here. The perimeter, however, cannot be found in closed form, as far as I know, except for special exponents.

We can solve for y as a function of x and find the arclength using the formula taught in calculus courses. However, the derivative of y has a singularity at x = 1. By switching to polar coordinates, we can find arclength in terms of an integrand with no singularities. We can also simplify things a little by computing the total arclength as 4 times the arclength in the first quadrant; this avoids having to take absolute values.

The following Python code computes the perimeter and the ratio of the area to the perimeter.

    from scipy import sin, cos, pi
    from scipy.integrate import quad
    from scipy.special import gamma
    
    def r(t, p):
        return (cos(t)**p + sin(t)**p)**-(1/p)
    
    def drdt(t, p):
        deriv = (cos(t)**p + sin(t)**p)**(-1-1/p)
        deriv *= cos(t)**(p-1)*sin(t) - sin(t)**(p-1)*cos(t)
        return deriv
    
    def integrand(t, p):
        return (drdt(t,p)**2 + r(t,p)**2)**0.5
    
    def arclength(p):
        integral = quad(lambda t: integrand(t,p), 0, pi/2)[0]
        return 4*integral
    
    def area(p):
        return 4*gamma(1 + 1/p)**2 / gamma(1 + 2/p)
    
    def ratio(p):
        return area(p) / arclength(p)

Basic geometry tells us the ratio is 1/2 when p = 2 and we have a circle. The ratio is also 1/2 when p = ∞, i.e. when we have a square. We can use the code above to find that the ratio when p = 0.528627, so there is at least one local maximum for values of p between 2 and ∞.

Here’s a plot of the ratio of area to perimeter as a function of p.

ratio of area to perimeter for squircle

The plot is quite flat for large values of p, but if we zoom in we can see that there is a local maximum near 4.4.

close up of previous graph near the maximum

When I find the maximum of the ratio function using Brent’s method (scipy.optimize.brent) I find p = 4.39365679, which agrees with the value Panholzer stated.

Here’s a plot of the squircle corresponding to this value of p.

squircle with largest area to perimeter ratio

Back to the isoparametric problem

Now why doesn’t this contradict the isoparametric problem? Area scales quadratically but perimeter scales linearly. If you don’t hold perimeter constant, you can find a larger ratio of area to volume by making the perimeter larger. And that’s what we’ve done. When p = 2, we have a unit circle, with area π and perimeter 2π. When p = 4.39365679 we have area 3.750961567 and permimeter 7.09566295. If we were to take a circle with the same perimeter, it would have area 4.00660097, larger than the squircle we started with.

More squircle posts

Exploring the sum-product conjecture

Posted on by John

Quanta Magazine posted an article yesterday about the sum-product problem of Paul Erdős and Endre Szemerédi. This problem starts with a finite set of real numbers A then considers the size of the sets A+A and A*A. That is, if we add every element of A to every other element of A, how many distinct sums are there? If we take products instead, how many distinct products are there?

Proven results

Erdős and Szemerédi proved that there are constants c and ε > 0 such that

max{|A+A|, |A*A|} ≥ c|A|1+ε

In other words, either A+A or A*A is substantially bigger than A. Erdős and Szemerédi only proved that some positive ε exists, but they suspected ε could be chosen close to 1, i.e. that either |A+A| or |A*A| is bounded below by a fixed multiple of |A|² or nearly so. George Shakan later showed that one can take ε to be any value less than

1/3 + 5/5277 = 0.3342899…

but the conjecture remains that the upper limit on ε is 1.

Python code

The following Python code will let you explore the sum-product conjecture empirically. It randomly selects sets of size N from the non-negative integers less than R, then computes the sum and product sets using set comprehensions.

    from numpy.random import choice

    def trial(R, N):
        # R = integer range, N = sample size
        x = choice(R, N, replace=False)
        s = {a+b for a in x for b in x}
        p = {a*b for a in x for b in x}
        return (len(s), len(p))

When I first tried this code I thought it had a bug. I called trial 10 times and got the same values for |A+A| and |A*A| every time. That was because I chose R large relative to N. In that case, it is likely that every sum and every product will be unique, aside from the redundancy from commutativity. That is, if R >> N, it is likely that |A+A| and |A*A| will both equal N(N+1)/2. Things get more interesting when N is closer to R.

Probability vs combinatorics

The Erdős-Szemerédi problem is a problem in combinatorics, looking for deterministic lower bounds. But it seems natural to consider a probabilistic extension. Instead of asking about lower bounds on |A+A| and |A*A| you could ask for the distribution on |A+A| and |A*A| when the sets A are drawn from some probability distribution.

If the set A is drawn from a continuous distribution, then |A+A| and |A*A| both equal N(N+1)/2 with probability 1. Only careful choices, ones that would happen randomly with probability zero, could prevent the sums and products from being unique, modulo commutativity, as in the case R >> N above.

If the set A is an arithmetic sequence then |A+A| is small and |A*A| is large, and the opposite holds if A is a geometric sequence. So it might be interesting to look at the correlation of |A+A| and |A*A| when A comes from a discrete distribution, such as choosing N integers uniformly from [1, R] when N/R is not too small.

RSA with one shared prime

Posted on by John

The RSA encryption setup begins by finding two large prime numbers. These numbers are kept secret, but their product is made public. We discuss below just how difficult it is to recover two large primes from knowing their product.

Suppose two people share one prime. That is, one person chooses primes p and q and the other chooses p and r, and q ≠ r. (This has happened [1].) Then you can easily find p. All three primes can be obtained in less than a millisecond as illustrated by the Python script below.

In a way it would be better to share both your primes with someone else than to share just one. If both your primes are the same as someone else’s, you could read each other’s messages, but a third party attacker could not. If you’re lucky, the person you share primes with doesn’t know that you share primes or isn’t interested in reading your mail. But if that person’s private key is ever disclosed, so is yours.

Python code

Nearly all the time required to run the script is devoted to finding the primes, so we time just the factorization.

    from secrets import randbits
    from sympy import nextprime, gcd
    from timeit import default_timer as timer
    
    numbits = 2048
    
    p = nextprime(randbits(numbits))
    q = nextprime(randbits(numbits))
    r = nextprime(randbits(numbits))                                      
    
    m = p*q
    n = p*r
    
    t0 = timer()
    g = gcd(m, n)
    assert(p == g)
    assert(q == m//p)
    assert(r == n//p)
    t1 = timer()
    
    # Print time in milliseconds
    print(1000*(t1 - t0))

Python notes

There are a few noteworthy things about the Python code.

First, it uses a cryptographic random number generator, not the default generator, to create 2048-bit random numbers.

Second, it uses the portable default_timer which chooses the appropriate timer on different operating systems. Note that it returns wall clock time, not CPU time.

Finally, it uses integer division // to recover q and r. If you use the customary division operator Python will carry out integer division and attempt to cast the result to a float, resulting in the error message “OverflowError: integer division result too large for a float.”

GCD vs factoring

If you wanted to find the greatest common divisor of two small numbers by hand, you’d probably start by factoring the two numbers. But as Euclid knew, you don’t have to factor two numbers before you can find the greatest common factor of the numbers. For large numbers, the Euclidean algorithm is orders of magnitude faster than factoring.

Nobody has announced being able to factor a 1024 bit number yet. The number m and n above have four times as many bits. The largest of the RSA numbers factored so far has 768 bits. This was done in 2009 and took approximately two CPU millennia, i.e. around 2000 CPU years.

Fast Euclidean algorithm

The classic Euclidean algorithm takes O(n²) operations to find the greatest common divisor of two integers of length n. But there are modern sub-quadratic variations on the Euclidean algorithm that take

O(n log²(n) log(log(n)))

operations, which is much faster for very large numbers. I believe SymPy is using the classic Euclidean algorithm, but it could transparently switch to using the fast Euclidean algorithm for large inputs.

Related posts

[1] As noted in the comments, this has happened due to faulty software implementation, but it shouldn’t happen by chance. By the prime number theorem, the number of n-bit primes is approximately 2n / (n log 2). If M people choose 2M primes each n bits long, the probability of two of these primes being the same is roughly

22-n M n log 2.

If M = 7.5 billion (the current world population) and n = 1024, the probability of two primes being the same is about 10-295. This roughly the probability of winning the Powerball jackpot 40 times in a row.

Searching for Mersenne primes

Posted on by John

The nth Mersenne number is

Mn = 2n – 1.

A Mersenne prime is a Mersenne number which is also prime. So far 50 51 have been found [1].

A necessary condition for Mn to be prime is that n is prime, so searches for Mersenne numbers only test prime values of n. It’s not sufficient for n to be prime as you can see from the example

M11 = 2047 = 23 × 89.

Lucas-Lehmer test

The largest known prime has been a Mersenne prime since 1952, with one exception in 1989. This is because there is an efficient algorithm, the Lucas-Lehmer test, for determining whether a Mersenne number is prime. This is the algorithm used by GIMPS (Great Internet Mersenne Prime Search).

The Lucas-Lehmer test is very simple. The following Python code tests whether Mp is prime.

    def lucas_lehmer(p):
        M = 2**p - 1
        s = 4
        for _ in range(p-2):
            s = (s*s - 2) % M
        return s == 0

Using this code I was able to verify the first 25 Mersenne primes in under 50 seconds. This includes all Mersenne primes that were known as of 40 years ago.

History

Mersenne primes are named after the French monk Marin Mersenne (1588–1648) who compiled a list of Mersenne primes.

Édouard Lucas came up with his test for Mersenne primes in 1856 and in 1876 proved that M127 is prime. That is, he found a 39-digit prime number by hand. Derrick Lehmer refined the test in 1930.

As of January 2018, the largest known prime is M77,232,917.

More prime number posts

[1] We’ve found 51 Mersenne primes as of December 22, 2018, but we’re not sure whether we’ve found the first 51 Mersenne primes. We know we’ve found the 47 smallest Mersenne primes. It’s possible that there are other Mersenne primes between the 47th and the 50th known Mersenne primes, and there may be one hiding between the 50th and 51st.

Ellipsoid distance on Earth

Posted on by John

globe

To first approximation, Earth is a sphere. But it bulges at the equator, and to second approximation, Earth is an oblate spheroid. Earth is not exactly an oblate spheroid either, but the error in the oblate spheroid model is about 100x smaller than the error in the spherical model.

Finding the distance between two points on a sphere is fairly simple. Here’s a calculator to compute the distance, and here’s a derivation of the formula used in the calculator.

Finding the distance between two points on an ellipsoid is much more complicated. (A spheroid is a kind of ellipsoid.) Wikipedia gives a description of Vincenty’s algorithm for finding the distance between two points on Earth using an oblate spheroid model (specifically WGS-84). I’ll include a Python implementation below.

Comparison with spherical distance

How much difference does it make when you calculate difference on an oblate spheroid rather than a sphere? To address that question I looked at the coordinates of several cities around the world using the CityData function in Mathematica. Latitude is in degrees north of the equator and longitude is in degrees east of the prime meridian.

    |--------------+--------+---------|
    | City         |    Lat |    Long |
    |--------------+--------+---------|
    | Houston      |  29.78 |  -95.39 |
    | Caracas      |  10.54 |  -66.93 |
    | London       |  51.50 |   -0.12 |
    | Tokyo        |  35.67 |  139.77 |
    | Delhi        |  28.67 |   77.21 |
    | Honolulu     |  21.31 | -157.83 |
    | Sao Paulo    | -23.53 |  -46.63 |
    | New York     |  40.66 |  -73.94 |
    | Los Angeles  |  34.02 | -118.41 |
    | Cape Town    | -33.93 |   18.46 |
    | Sydney       | -33.87 |  151.21 |
    | Tromsø       |  69.66 |   18.94 |
    | Singapore    |   1.30 |  103.85 |
    |--------------+--------+---------|

Here are the error extremes.

The spherical model underestimates the distance from London to Tokyo by 12.88 km, and it overestimates the distance from London to Cape Town by 45.40 km.

The relative error is most negative for London to New York (-0.157%) and most positive for Tokyo to Sidney (0.545%).

Update: The comparison above used the same radius for both the spherical and ellipsoidal models. As suggested in the comments, a better comparison would use the mean radius (average of equatorial and polar radii) in the spherical model rather than the equatorial radius.

With that change the most negative absolute error is between Tokyo and New York at -30,038 m. The most negative relative error is between London and New York at -0.324%.

The largest positive error, absolute and relative, is between Tokyo and Sydney. The absolute error is 29,289 m and the relative error is 0.376%.

Python implementation

The code below is a direct implementation of the equations in the Wikipedia article.

Note that longitude and latitude below are assumed to be in radians. You can convert from degrees to radians with SciPy’s deg2rad function.

from scipy import sin, cos, tan, arctan, arctan2, arccos, pi

def spherical_distance(lat1, long1, lat2, long2):
    phi1 = 0.5*pi - lat1
    phi2 = 0.5*pi - lat2
    r = 0.5*(6378137 + 6356752) # mean radius in meters
    t = sin(phi1)*sin(phi2)*cos(long1-long2) + cos(phi1)*cos(phi2)
    return r * arccos(t)

def ellipsoidal_distance(lat1, long1, lat2, long2):

    a = 6378137.0 # equatorial radius in meters 
    f = 1/298.257223563 # ellipsoid flattening 
    b = (1 - f)*a 
    tolerance = 1e-11 # to stop iteration

    phi1, phi2 = lat1, lat2
    U1 = arctan((1-f)*tan(phi1))
    U2 = arctan((1-f)*tan(phi2))
    L1, L2 = long1, long2
    L = L2 - L1

    lambda_old = L + 0

    while True:
    
        t = (cos(U2)*sin(lambda_old))**2
        t += (cos(U1)*sin(U2) - sin(U1)*cos(U2)*cos(lambda_old))**2
        sin_sigma = t**0.5
        cos_sigma = sin(U1)*sin(U2) + cos(U1)*cos(U2)*cos(lambda_old)
        sigma = arctan2(sin_sigma, cos_sigma) 
    
        sin_alpha = cos(U1)*cos(U2)*sin(lambda_old) / sin_sigma
        cos_sq_alpha = 1 - sin_alpha**2
        cos_2sigma_m = cos_sigma - 2*sin(U1)*sin(U2)/cos_sq_alpha
        C = f*cos_sq_alpha*(4 + f*(4-3*cos_sq_alpha))/16
    
        t = sigma + C*sin_sigma*(cos_2sigma_m + C*cos_sigma*(-1 + 2*cos_2sigma_m**2))
        lambda_new = L + (1 - C)*f*sin_alpha*t
        if abs(lambda_new - lambda_old) <= tolerance:
            break
        else:
            lambda_old = lambda_new

    u2 = cos_sq_alpha*((a**2 - b**2)/b**2)
    A = 1 + (u2/16384)*(4096 + u2*(-768+u2*(320 - 175*u2)))
    B = (u2/1024)*(256 + u2*(-128 + u2*(74 - 47*u2)))
    t = cos_2sigma_m + 0.25*B*(cos_sigma*(-1 + 2*cos_2sigma_m**2))
    t -= (B/6)*cos_2sigma_m*(-3 + 4*sin_sigma**2)*(-3 + 4*cos_2sigma_m**2)
    delta_sigma = B * sin_sigma * t
    s = b*A*(sigma - delta_sigma)

    return s